リーマン仮説（リーマン予想）の証明　ver20

証明の第２部以降を見たい方はページの最後にある目次をクリックしてください。





ver15には不充分なところが見つかりました。そこで、それを修正するためにいろいろ試しているうちに ver20　になってしまいました。そろそろ証明にも疲れてきたので、これが失敗なら、このあたりでひとまずお休みにしようかと考えています。・・・とは言うものの、このver20は結構うまくいっていると思うのですが、どうでしょうか。

ver14から微分零線を使う証明にトライしていますが、ver15ですべての事例の検討を終わらせたつもりでした。しかし、検討を続けるうちに、私が予想もしない事例が残っていることに気が付きました。この事例は、一見してあり得ないのですが、証明となると、なかなか手がかりを与えてくれません。結局、この事例のおかげで微分零線を使う証明を諦めることになりました。

もちろん、今まで扱った事例については有効ですから、リーマン仮説証明の大部分は微分零線方式で証明したことになります。ただ、最後の残りの事例については、別のやり方を導入したと言うことです。この新たに採用したやり方はサイクル（周期）を使うやり方で、まだ慣れてないので思わぬ誤解があるかも知れませんが、それほど複雑な論理ではないので、証明の適否はすぐに判明するだろうと思います。

相変わらず自信だけはあるので、今回も「完全証明」と言いたいところですが、判断は皆様にお委ねすることにします。問題点、疑問点があるならご指摘いただけると幸いです。

最近は、「こいつに間違いを教えると、かえって頑張り出す。」と思うのか、間違いを指摘してくれる人が少なくなりました。（ＴＴ）　おかげで間違いを自分で見つけるのにとても時間がかかるようになりました。それだけ高度なレベルに達したと言うことでしょうか。
（＾＾）　　何事も楽観的に考えるべきですね。




第１部　　　　　　証明の概略



■１の１■　　　　　　初めに


リーマン仮説（予想）証明については、目くら蛇に怖じずの精神で頑張りましたが、やっぱり難しいですね。今回ver20になりましたが、番号を付けなかった失敗例もたくさんあるので、アイデアとしてはかなりの数をトライしたと思います。そのうちのひとつかふたつは今でもまだ有望だと思うのもありますが、ほとんどすべて失敗しました。しかし、最後の最後に、何とか証明に辿り着けたのはまったく幸運だったとしか言いようがありません。

以前書いた「証明の概略」はリーマン仮説をまだ良く知らない人のためにと思って作ったページですが、私自身がリーマン仮説についてよく判っていないことがだんだんわかってきました。（〜〜）ですから、ここでは説明というより雑談になるのですが、どこに問題があるかをなるべく明らかにしておきたいと思います。




■１の２■　　　　　　リーマン仮説なのか、リーマン予想なのか？

日本では「リーマン予想」という言い方が普通ですが、英語では「Riemann Hypothesis」となっています。直訳すると「リーマン仮説」です。どこから「リーマン予想」という単語が生まれたのでしょうか。「予想」は英語で expectation, conjecture などで、数学としては相応しい単語ではありません。なので私としては「リーマン仮説」という言い方を使うことにしました。




■１の３■　　　　　　リーマン仮説の定義


リーマン仮説が何であるかは自明であると思っていましたが、私の理解が少し違っていたかもしれません。おそらく「仮説」と言うか、「予想」と言うかで理解が異なるのでしょうが、ウィキペディアによると、「ζ(s) の自明でない零点 s は、全て実部が 1/2 の直線上に存在する。」と説明されていました。誰に教わったのか忘れましたが、私の理解では
「自明でない零点はa=0.5上以外に存在しない。」というものです。同じことのように聞こえるかもしれませんが、証明の手順が異なります。

重要な相違点は、「a=0.5以外に存在しない」ことが証明されても、それがただちに「a=0.5上に存在する」証明にはならないことです。ひとつも存在しないかもしれないからです。

「a=0.5上にリーマン零点が無限に存在することはすでに証明されている」との指摘を受けています。その証明の中身はまだ知りませんが、そうなのかもしれないと思います。　　　 （付記）　　　私なりの証明方法を思いついたので、参考までにこの証明の付録として載せておきます。最後の結論のあとに付け加えました。　　　　 しかし、存在証明とリーマン仮説証明とは概念的に別のものです。論理の手順として、a=0.5上以外に存在しないことを証明しただけで完成するか、それとも、不存在証明のあとにa=0.5上に存在することの証明を付け加えるべきなのかという問題です。とは言うものの、存在証明は、ひとつでもリーマン零点が存在すればよいのですから、あまり難しい証明ではありません。結局、どちらの理解でも手間としてはたいした違いは生じません。

定義は、真理問題ではないので、どちらが正しいと言うことではないはずです。どちらがより一般的かということなのでしょう。とするとウィキペディアの説明のほうが一般的となります。ただ、私としては、「a=0.5以外に零点はない」という理解で進んできたので、ここでは不存在証明のほうに焦点を合わせています。そして不存在証明のあとで、付録のような形で存在証明を付け加えることで一般的理解に合わせておきました。というわけで、この証明の中では不存在証明をリーマン仮説証明と呼ぶ場合が多いことをご了承下さい。





■１の４■　　　　　　ゼータ関数とは？

それから、結構大きな問題はゼータ関数の定義です。当初、私は単純にΣ1/n^rのことだと理解していましたが、何人かの人に指摘していただき、Σ_[n=1,∞]1/n^r が正しい理解であると教えられました。単純な理解のほうが判りやすいとも思いますが、数学者の方々がそう理解しているなら仕方ありません。

しかし、問題はさらに続きます。このゼータ関数はリーマン零点を計算する式としてのゼータ関数ではないということです。リーマン零点はゼータ関数を解析接続したあとに出来た式を零とする点です。この場合、解析接続後に出来た式をゼータ関数と呼ぶ場合があります。この呼び名ははなはだ問題で、混乱の元です。解析接続前の式と後の式では内容が異なるのですから、同じ名前で呼ぶべきではありません。私としては混乱を避けるために解析接続前の式をゼータ関数と呼び、後の式をk(s)と呼ぶことにしています。

もっとも、以上の説明はあとから付けたもので、私は解析接続の内容をまったく知りませんし、その結果の式が何であるかも知りません。ただ、私が別のテーマで研究していたk(x)がたまたま解析接続後の式と同じである可能性があるので、便宜上、上記のような説明をさせていただきました。間違いのない説明だと思いますが、保証の限りではありません。

k(s)を使ったリーマン零点の計算方法については別ページで説明してありますが、それは最初の頃に書いた説明なのでかなり素朴な内容になっています。判りにくいとの指摘も受けたので、なるべく判りやすくなることを願って、ここに再度解説をしておきます。




■１の５■　　　　リーマン零点の計算方法


k(x)を発見したきっかけは、ゼータ関数を正の実数で計算するとき、いかにして速やかに収束させるかを研究したことです。k(x)=Σ_[n=1,∞]1/n^x とすると、k(2)=1.64493、k(4)=1.08232 であることは計算によりすぐに求められます。k(1.5)を計算したところ、10項まで計算して1.99533 となり、なかなか収束してくれません。そこで収束の過程を調べたところ、
Σ1/n^x = k(x) - 1/(x-1)/n^(x-1) + 1/2/n^x - x/12/n^(x+1) + 0 + x*(x+1)*(x+2)/6!/n^(x+3) + 0 + .....
という式を見つけました。当時たまたまsu(r)という数列を研究していたのですが、上記の式をsu(r)で綺麗に表現できるのでとても嬉しく思いました。このsu(r)はベルヌーイ数とほとんど同じものなのですが、ベルヌーイ数を当時は知らなかったので第５の広場　２）のような説明になりました。

これをベルヌーイ数で表記すると以下のようになります。

Σ1/n^x = k(x) - B(0)/(x-1)/n^(x-1) - B(1)/n^x - B(2)*x/2!/n^(x+1) - 0 - B(4)*x*(x+1)*(x+2)/4!/n^(x+3) - 0 - .....

xが１以下やマイナスでもこの公式が使えるということに気がついたのは後のことですが、xが何であれ速やかに結果が出てきます。たとえば、k(0)=-0.5 、k(0.5)=-1.4603545088... となります。複素数は私の研究対象外だったのですが、あることがきっかけで複素数に拡大してみたところ、リーマン零点と同じ場所に零点が見つかりました。いくつもの零点が一致するのですから、複素数に拡張したk(s)こそ接続解析後の式そのものだと言って間違いないと思います。

s=a+bi としてk(s)を表記すると次のようになります。
Σ1/n^s = k(s) - 1/(s-1)/n^(s-1) + 1/2/n^s - s/12/n^(s+1) + 0 + s*(s+1)*(s+2)/6!/n^(s+3) + 0 + .....

これをもとにしてどのようにリーマン零点を計算するか・・・ですが、k(s)の計算式は長いので、それを分割して　Σ1/n^s部分をzt(s,n)、残りの部分をber(s,n)とします。つまり、

k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }

となります。

zt(s,n) = 1 + 1/2^s + 1/3^s + . . . + 1/n^s
ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r
となります。

n^s=n^a*n^bi です。n^bi = cos(b*ln(n)) + i * sin(b*ln(n)) です。1/n^bi は分子分母にcos(b*ln(n)) - i * sin(b*ln(n))　を掛けると分母が１となるので、1/n^bi = cos(b*ln(n)) - i * sin(b*ln(n)) となります。

ですから、zt(s,n)の実部は　1 + cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... + cos(b*ln(n))/n^a 　となります。虚部は　- { sin(b*ln(2))/2^a + sin(b*ln(3)))/3^a + . . . + sin(b*ln(n))/n^a } となります。

zt(s)の実部式をzt_re(a,b)、虚部式をzt_im(a,b) とします。すると以下のように表記できます。

zt_re(a,b,n) = 1 + cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... + cos(b*ln(n))/n^a 　

zt_im(a,b,n) = - { sin(b*ln(2))/2^a + sin(b*ln(3)))/3^a + . . . + sin(b*ln(n))/n^a




■１の６■　　　　　　ber(s,n)　の計算方法

ber(s) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r
であることはすでに述べています。ベルヌーイ数も再掲しておくと、B(0)=1, B(1)=-1/2, B(2)=1/6, B(4)=-1/30, B(6)=1/42, B(8)=-1/30, B(10)=5/66, . . . ということで、詳しくは「ベルヌーイ数」を参照してください。

(s-2+r)!/(s-1)! を複素数として計算するのは面倒です。r=0のとき1/(s-1), r=1のとき1, r=2のときs, r=3のとき(s+1)*s, r=4のとき(s+2)*(s+1)*s, . . . と変化します。そこで計算がしやすいように、ra(r), rb(r)を定義することにします。

(s-2+r)*(s-2+r-1)*(s-2+r-2)*....*(s+1)*sの実部をra(r), 虚部をrb(r) と定義します。つまり、

(s-2+r)*(s-2+r-1)*(s-2+r-2)*....*(s+1)*s = ra(r)+rb(r)*i となります。

A=a-1, H=A^2+b^2 とすると、ra(0)=A/H, rb(0)=-b/H です。ra(1)=1, rb(1)=0 はすぐ判ります。r=2 から先は面倒な計算が必要になります。

そこで計算過程を明確にするためにka(n,r)を定義します。このka(n,r)は (n+1)*(n+2)*(n+3)* ... を展開するときに現れる係数です。

ka(0,0)=1,
ka(1,0)=1, ka(1,1)=1,
ka(2,0)=1, ka(2,1)=3, ka(2,2)=2,
ka(3,0)=1, ka(3,1)=6, ka(3,2)=11, ka(3,3)=6,
ka(4,0)=1, ka(4,1)=10, ka(4,2)=35, ka(4,3)=50, ka(4,4)=24,
以下略。
ka(n,r)は、ka(n,r) = n*ka(n-1,r-1) + ka(n-1,r) として計算することも出来ます。

ra(2)=a,　rb(2)=b　です。

r=4のとき、

(a+bi)^3, (a+bi)^2, (a+bi), を展開し、次のようにka(n,r)を掛けて並べます。
ka(2,0) * { a^3+3a^2(bi)+3a(bi)^2+(bi)^3 }
ka(2,1) * { a^2+2a(bi)+(bi)^2 }
ka(2,2) * { a+(bi) }
この式の実部を総計したものがra(4)　虚部を計算するとrb(4) となります。
この場合、ka(2,0)=1,ka(2,1)=3,ka(2,1)=2, ですから、
ra(4)=a^3-3ab^2+3a^2-3b^2+2a,　 rb(4)=3a^2*b+6ab+2b-b^3, となります。

r=5 ならば、
ka(3,0) * { a^4+4a^3(bi)+6a^2(bi)^2+4a(bi)^3+(bi)^4 }
ka(3,1) * { a^3+3a^2(bi)+3a(bi)^2+(bi)^3 }
ka(3,2) * { a^2+2a(bi)+(bi)^2 }
ka(3,3) * { a+(bi) }
この場合、ra(5)=a^4+6a^3-6a^2b^2+11a^2+6a-18ab^2+b^4-11b^2
rb(5)=4a^3b-4ab^3+18a^2b-6b^3+22ab+6b
となります。

r=6 ならば、
ka(4,0) * { a^5+5a^4(bi)+10a^3(bi)^2+10a^2(bi)^3+5a(bi)^4+(bi)^5 }
ka(4,1) * { a^4+4a^3(bi)+6a^2(bi)^2+4a(bi)^3+(bi)^4 }
ka(4,2) * { a^3+3a^2(bi)+3a(bi)^2+(bi)^3 }
ka(4,3) * { a^2+2a(bi)+(bi)^2 }
ka(4,4) * { a+(bi) }

ra(6)=a^5-10a^3b^2+5ab^4+10a^4-60a^2b^2+10b^4+35a^3-70ab^2+50a^2-50b^2+24a
rb(6)=5a^4b-10a^2b^3+b^5+40a^3b-40ab^3+105a^2b-35b^3+100ab+24b

以下、同じやり方でどこまでも計算できます。ただし計算時間が掛かるので、実際はプログラム化して処理します。

このra(r), rb(r)　を用いて表記すると、　ber(s,n) = B(0)*(ra(0)+rb(0)*i)/0!/n^0/n^(s-1) + B(1)*(ra(1)+rb(1)*i)/1!/n/n^(s-1) + B(2)*(ra(2)+rb(2)*i)/2!/n^2/n^(s-1) + ....　となり、この中のn^(s-1)にも虚数が含まれるのでさらに整理します。

さて、ber(s,n)のうち実部について纏めたものをber_re(a,b,n) とします。 P=cos(b*ln(n)), Q=sin(b*ln(n)), A=a-1, H=A^2+b^2　とすると次のように表記できます。

ber_re(a,b,n) = (A*P-b*Q)/n^A/H - P/2/n^a + B(2)*(P*a+Q*b)/2!/n^2/n^A + B(4)*{P*ra(4)+Q*rb(4)}/4!/n^4/n^A + B(6)*{P*ra(4)+Q*rb(6)}/6!/n^6/n^A +....

ber_re(a,b,n) = Σ_[r=0,∞] B(r) * (P*ra(r) + Q*rb(r)) /r!/n^r/n^A

虚部について纏めたものをber_im(a,b,n) とします。

ber_im(a,b,n) = (-b*P-A*Q)/n^A/H + Q/2n^a + B(2)*(P*b-Q*a)/2!/n^2/n^A + B(4)*(P*rb(4)-Q*ra(4))/4!/n^4/n^A + B(6)*(P*rb(6)-Q*ra(6))/6!/n^6/n^A + ....

ber_im(a,b,n) = Σ_[r=0,∞]　B(r) * (P*rb(r) - Q*ra(r) /r!/n^r/n^A


ber(s,n)の計算式の中にベルヌーイ数が登場します。この数はあるところまでは収束します。しかし、そのうちに急激に増加し始め、ついには振動・発散してしまいます。ですから、rを∞まで計算すると答えが出ません。そこで、適当なところで計算をうち切って、zt(s,n)の計算結果と合計してk(s)の答えを得ます。「そんないい加減な・・・」と言われてしまうでしょうが、k(s)=lim_[n→∞] zt(s,n)+ber(s,n)　の式の中にある n→∞ でベルヌーイ数の振動・発散が吸収されるので、これで何ら問題なく正しい答えを得ることが出来るのです。

計算精度が必要な場面では結構面倒な議論が必要になりますが、一般的にはrをどこで切っても結果に差はありません。私の場合はr=n*2あたりで切ることにしています。

これをもとにプログラムを作って計算したところ、実部の零点は、0.81954532942, 14.1347251421, 14.5179196271, 20.6540449693, 21.0220396387, 25,0108575801, 25.4915082146 と並んでいることが判りました。

虚部の零点を計算しましたが、3.43621822608, 9.66690805613, 14.1347251417, 17.8455995404, 21.0220396387, 23.1702827011, 25.0108575801, 27.6701822176, と並んでいました。同じ値のところがリーマン零点となります。

k(s)の計算プログラムは　私の発見した数学公式　付録２」の「Javaによる多桁計算ソフトの使い方」の中にあるので、ダウンロードできます。





■１の７■　　　　　　複素数における零点の法則


さて、リーマン仮説証明のためには複素数の性質や法則を知っておく必要があります。

私はもともと、複素数には関心がなく、もっぱら実数の範囲で公式研究をしていた関係で、複素数についての知識はリーマン仮説証明をトライする過程で学びました。ですから、足りないところだらけで、この証明を公表した当初は、考え方や表記の仕方について数多くのご批判をいただきました。その批判によって初めて判ったことがたくさんありました。感謝いたします。以下の説明も、我流の域を出ませんが、ご容赦下さい。

複素数a+biが零であるとは、a=0 かつ b=0　ということです。そして、複素数zが零の時、任意の複素数x に対して、x*z=0 となり、x/z は計算不能となるのは実数の時と同じです。交換法則や結合法則も成り立ちます。そして、x*y=0 の時、　x=0　もしくはy=0　であることも実数と同じです。x≠0　かつ y≠0 のとき、x*y≠0 であることも実数と同じです。

また、(c+di)/(a+bi)において、a+bi=0なら、無限大になるというのが実数での結論ですが、複素数では、分子・分母に(a-bi)を掛けて、(c+di)*(a-bi)/(a^2+b^2)という形に導きます。分子は(ac+bd)+(ad-bc)*i となります。a+bi=0ですから、a=0, b=0 なので、分子も零となり、0/0という結論になります。ですから、必ずしも無限大になるとは限りません。

また、実数なら、無限大で割ると零となりますが、複素数では必ずしも零にはならないことも注意が必要です。また、実数では、２乗は必ずプラスですが、複素数ではx=a+bi ですから、x^2=(a^2-b^2)+2abi となり、マイナスになる可能性もあります。

なお、複素数の表記法ですが、a+bi のことを(a,b)と書くことも出来るとのことなので、適宜そのようにしたところもあるので、ご了解ください。




■１の８■　　　　　　複素空間で複素数の動きを調べる

実数関数ではXY座標を使って関数の形を調べます。私もXY座標の威力に感心した人間のひとりで、これを発案したデカルトを深く尊敬しています。XY座標は、数学の本質を変えるものではありませんが、これにより数学を判りやすくすると言うことにおいて絶大な貢献をはたしました。数学史の本を開けてみると、このXY座標の発案についての記述があまりないのですが、これについては是非触れて欲しいと思います。

さて、XY座標と同じアイデアを複素数にも導入したいのですが、複素関数では、x、y のそれぞれにa, b という二つの要素があり、合計４つの要素を考えなければなりません。しかし、平面で使えるのは２つ、空間の場合は３つしか扱えません。何かよい方法はないだろうかと模索しているのですが、なかなかこれと言ったものが見つかりません。やむを得ず、ここでは複素空間というアイデアを使うことにします。

複素空間は、XYZ座標と同じことですが、ただ、ふたつのXYZ座標を重ねて理解するという特徴があります。つまり、複素関数のxには(a1, b1)という要素があるので、a1をX軸、b1をY軸として、平面全体をa1+b1*i と対応させます。xが定まると、それに対応している平面上の点が定まることになります。さて、yにもふたつの要素があるので、(a2, b2) と表現します。このa2とb2をZで対応させます。つまり、yの実部であるa2を意味するZ座標と、虚部のb2を意味するZ座標のふたつを想定するのです。これで、複素数x, y がXYZ座標と対応関係を持つことができるようになります。

ひとつの関数にふたつの空間を想定するのはやや不便ですが、いまのところ仕方ありません。これを使って複素関数の姿をなんとか捉えてみたいと思います。

s=a+bi のaをX軸、bをY軸とするので、XY平面をab平面と呼ぶことがあります。また、Z軸にはz1,z2が対応していますが、単にzと表記する場合があることをご了解下さい。





■１の９■　　　　　　リーマン零点とは


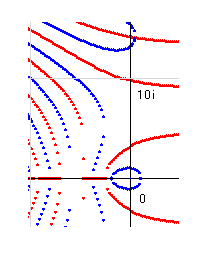
さて、k(x)を複素数に拡大してk(s)とし、s=a+bi 、k(s)=z1+z2*i と理解します。k(s)が零となるのが零点ですから、z1=0 かつ z2=0 ということです。これを視覚的に理解するために、まずはXYz1座標においてz1=0となるようなa, b を探します。そのようなa, b をXY座標で表し、複素平面図を描いてみます。これを実零線と名付けます。また、XYz2座標でも同じようにz2=0となるような図を色を変えて描いてみます。これを虚零線と名付けます。

そのふたつを重ねたとき、その交点がz1=0, z2=0 となっているので、そこが零点であることが判ります。より詳細な図が見たい方は「証明第４部」をご覧ください。この図を見ると、実部と虚部の交点がa=0.5の線上にあることが判ります。

零点は、b=0 つまり実数の線上にもあります。この零点のことを「自明の零点」と呼ぶそうです。英語では　the trivial zeros となっていました。ずいぶんニュアンスが違いますね・・・・。それはそれとして、「自明でない零点（the non trivial zeros）はa=0.5上以外に存在しない。」ということがリーマン仮説の内容ですから、それを証明することがここでの目標になります。

なお、複素数においては、実部が零となる点と虚部が零となる点があり、それらを零点と呼ぶこともありますが、この証明ではそれぞれ「実部の零点」、「虚部の零点」と呼び、どちらも零のところは「リーマンの零点」もしくは「実虚零点」と呼んで区別しています。ただ、文脈上明らかなときは「実部のみの零点」を「零点」と呼ぶこともあるので、そのあたりは臨機応変に解釈していただければと思います。




■１の１０■　　　　　　k(s)=f(s)*g(s)　となるf(s), g(s) を見つける

さて、リーマン仮説を証明するやり方として最初にトライした方法は、k(s)=f(s)*g(s)　となる f(s), g(s) を見つけることです。これは結果的に失敗というか、作業の途中で諦めて、今回は別のやり方でトライしています。ただ、大変魅力的方法であることは変わりませんので、少しだけ紹介しておきます。

実数の場合、z≠0を証明するためには、z=x*y の式に於いて、x≠0 かつ y≠0 を証明することになります。これをそのまま関数に応用し、f(x)とg(x)がともに零とならないことが証明できれば、それがk(x)が零にならない証明となります。複素数関数でも同じことです。

そこで、k(s)=f(s)*g(s)となるf(s), g(s)を探したのですが、最初に見つけたのは、k(s)=zt(s-0.5)*hk(s) という式でした。

zt(s-0.5) = Σ1/n^(s-0.5)

hk(s) = 1 + (√2-1)/2^s + (√3-1)/3^s - (√2-2)/4^s + (√5-1)/5^s + ... という式です。

これは、zt(s-0.5)も、hk(s)も綺麗な式に因数分解できるので、とても魅力的でしたが、証明としてはうまくいきませんでした。




■１の１１■　　　　　　k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x }

ここからが第２部となります。

そこで、さらに別の式を求めて彷徨ったのですが、k(s)=f(s)*g(s) の反省から、x<1　で収束する式を見つけなければならないことが判りました。そういう方針のもとに探していると、k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } 　という式を見つけました。これは近似式ではなく、まったくのイークォルですから、複素数に拡張して使うことが出来ます。

k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } 　となります。ここに、s! という複素数階乗が登場しますが、これについては私自身の学びが足りないので、充分な説明は出来ません。ただ、k(s)は計算可能なので、s!は計算可能となります。ですから、この式を複素数階乗の定義として使うことが出来るはずです。これで今のところ矛盾無く計算できるので、この証明では一応、これが正しいとの前提で進めさせていただきます。

この式を使ってk(1-s)/k(s)≠0を証明することができます。途中で、マイナス階乗の公式などを使いますが、これについては「証明の第２部」を参照してください。

＜追加説明＞　　　kv(s) = k(1-s)/k(s)　ということです。




■１の１２■　　　　　　a<0、　1<a　 に零点がないことを証明します。

これが第３部となります。

さて、証明のひとつのステップとして、まずは　a>1 、0>a に零点がないことを証明しておきます。これについては、k(s) = 2^s/(2^s-1) * 3^s/(3^s-1) * ..... という式を使います。これは良く知られた式とのことで、a>1 で成り立ちます。この右辺の項目のそれぞれが零にならないことはすぐに証明できます。次に複素数をベクトルとして捉え、複素数の絶対値がベクトルの長さになるので、それを考慮した上で、零にならない項目を無限に掛け合わせたとき、そのベクトルの長さが１以上なので、零にならないことが証明できます。

k(1-s)/k(s)≠0　ですから、a>1 で零にならなければ、a<0 にも零はありません。




■１の１３■　　　　　　k(1-s)=0 なら　k(s)=0

さて、k(1-s)/k(s)≠0　が証明できたのですから、第一印象としては　k(1-s)≠0 は当然の結論のように思えます。しかし、k(1-s)=0 かつ k(s)=0 のとき、0/0 が発生して、k(1-s)/k(s)≠0 であるにも関わらずk(1-s)=0, k(s)=0 が成り立つ可能性が生じます。ですから、リーマン仮説完全証明のためには、k(1-s)/k(s)≠0　を前提にして、さらに次の証明を付け加えなければなりません。


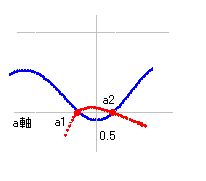
しかし、そうは言うものの、k(1-s)/k(s)≠0 は非常に重要な証明の通過点です。これにより、リーマン零点が存在するなら、k(1-s)=0, k(s)=0 という形でしか存在し得ないことになるからです。つまり、a=0.5上にあるなら零点はひとつですが、a=0.5上でなければ、「a=0.5の両側の等距離の所にペアで零点が発生すること」が明らかになりました。これは証明としては大進歩です。右図は、もしあったとしたらという仮定のもとで作った仮の図ですが、a=0.5を中心に左右等距離のところに零点が発生しています。このようなことが起こり得ないことをどうやって証明するかが次の課題となります。





■１の１４■　　　実零線・虚零線と零点の数

ここからが証明の第４部となります。

ここではab平面上の実零線・虚零線の形を分析します。この分析結果を用いて、第５部の証明へと移るので、ここは非常に重要です。

実零線とは、実部が零である点をab平面上に描くと現れる線のことです。虚零線は、虚部が零の線です。「１の９」に零線図を載せてありますが、実零線はマイナス無限からa=0.5あたりまで伸びてきて横Ｕ字形となるか、b=0の線と交わって上下対称の図になるかのいずれかです。虚零線はマイナス無限からプラス無限へと繋がる線が基本ですが、横Ｕ字形になるものもあり、また、b=0の軸と交わるのもあり、それにそもそもb=0の線が虚零線でもあります。

この実虚零線図を見るだけでふたつ横に並ぶリーマン零点は無さそうだとの印象を受けますが、証明となると、このあり得ないと思うことも論理化しなければなりません。



■１の１５■　　　k(s)を微分する

これからが第５部となります。

k(s)の実部は k_re(a,b)、虚部は k_im(a,b) と表記しますが、これをそれぞれ aについてと、bについて微分します。合計４つの微分式が得られます。

k_re(a,b)をaについて微分した式をk_re_a(a,b)とします。bについて微分した式をk_re_b(a,b)とします。

k_im(a,b)をaについて微分した式をk_im_a(a,b)とします。bについて微分した式をk_im_b(a,b)とします。

これらをプログラム化して計算し、式を分析したところ、何と！ 　k_re_a(a,b)=k_im_b(a,b)、k_re_b(a,b)=-k_im_a(a,b) が成り立つことが判りました。　ヽ(ﾟДﾟ)ﾉ !! 　「こういうことがあるのか」と驚かされる結論ですが、式の内容からも証明できます。

さて、微分とはXY座標においては傾きを求めることですから、微分式＝０の場所はk(s)の波の頂点を示しています。そこで、この零となる場所を、aについての微分と、bについての微分に分けて計算すると、それぞれの微分零線を描くことが出来ます。そして、この微分零線は実零線、虚零線と深い関係にあることが判りました。つまり、aについて微分した式の零線は実零線の上下に膨れた先端を必ず通ります。また、bについて微分した式の零線は実零線の左右に膨れた先端を通ります。

k(s)の場合、k_re_a(a,b)とk_im_b(a,b)がまったく同じ式なので、この零線は実零線の上下の先端を通過するだけでなく、虚零線の左右の先端も通過しています。これは図でも確認できます。同じように、k_re_b(a,b)とk_im_a(a,b)の式はマイナスを介して等しくなっています。値は逆ですが、零線の場所は同じです。この零線は実零線の左右の先端を通過し、かつ、虚零線の上下の先端を通過することになります。




■１の１６■　　　もし、リーマン零点がふたつあるなら。

微分零線との関係を念頭において、実零線・虚零線図を分析すると、リーマン零点がどうしてもa=0.5上にしかありえないことが見えてきます。ペアで存在することはありません。なぜなら、もし、リーマン零点が横に並んでふたつあるなら、そこを実零線も虚零線も通ることになります。すると、図では実零線も虚零線も波になっているので、ふたつの零点の間に必ず膨らみの先端が発生します。それが左右の先端であれ、上下の先端であれ、そこを微分零線が通過します。ところが、この微分零線は実零線と虚零線の作る枠から出ることが出来なくなります。なぜなら、実零線、虚零線と交差するためには、上下・左右の膨らみの先端が必要だからです。ここに矛盾が生じます。この現象を使うと、リーマン零点がふたつでは不都合が生じることを示すことが出来ます。

このやり方はとてもうまくいったと思います。最初に予想した零線図において矛盾を指摘できました。しかし、横Ｕ字形がふたつ横に並ぶ形の零線図の場合だけは矛盾を見つけられませんでした。そこで、これについては別の証明方法を検討することにしました。




■１の１７■　　　k(1-s)/k(s)　の実零線・虚零線

k(s)に横に並ぶリーマン零点があるなら、k(s)*k(1-s)にもあるはずです。そこに矛盾が生じるのではないかと思い分析してみましたが、k(s)で見つからない事例についてはk(s)*k(1-s)でも見つかりませんでした。k(1-s)/k(s)は第２部で使った公式でリーマン零点が無いことが証明されています。当初この式は無視していましたが、検討した式のすべてでうまくいかなかったので、この式もついでに検討したところ、リーマン零点が無いのでかえって矛盾が発生しやすいことに気がつきました。k(1-s)/k(s)の微分零線は奇妙な形に曲がりくねっています。矛盾もたくさんありそうに見えました。しかし、さらに検討を加えたところ、驚いたことに、曲がりくねらさなくても微分零線が引ける事例が見つかりました。これでは矛盾が発生するはずはありません。




■１の１８■　　　サイクル（周期）を使う証明

k(1-s)/k(s)での証明が失敗した時点で、この証明を諦めかけたのですが、どう見ても「ありえない」としか言いようのない図を見ながら、「どうしてあり得ないと思うか？」を考えました。それは波のリズムがその部分だけ異常に変化しているからです。そのリズムを数学的言葉に代えると「サイクル」（周期）となるのでしょうか。用語の点ではまだ確信がありませんが、とにかく、２サイクル分がこの箇所だけ１サイクルに減少しています。これは矛盾ではないでしょうか。

問題はそれをどうやって証明するかですが、幸い、k(1-s)/k(s)とk(s)は同じサイクルで動いています。また、虚零線の零点が１サイクルごとに一致します。ですから、全体的サイクルの一致は証明できます。この箇所だけはサイクルの一致が壊れています。これは矛盾として認定して良いのではないでしょうか。つまり、リーマン零点が横に並んで存在するところでは、必ずk(s)とk(1-s)/k(s)のサイクルが異なります。しかし、一方でk(s)とk(1-s)/k(s)のサイクルの一致は証明されています。これは矛盾です。

これで問題事例の証明が終わり、その他の事例についてはすでに微分零線の方法ですべて矛盾を指摘したのですから、実零線・虚零線図のすべての想定可能な形において矛盾を指摘できたことになります。すると、仮定法の前提として仮定した「リーマン零点がa=0.5から等距離のところに横に並んで存在する」という命題が成り立たないことの証明が完成したことになります。

以上の解説で興味を持った人は、証明の本体をご覧ください。質問や疑問点、間違い箇所の指摘は大歓迎ですので、遠慮なく下記のアドレスにメールをいただければと思います。

間違った証明を何度も載せたので、もう信用度はかなり落ちていることと思いますが、（TT)　寛容にお付き合いいただければと思います。




＜追加＞

■１の１９■　　　ver36 の証明

「１の１８」までは ver20 の証明です。「サイクルが乱れることはない」という前提で証明を完成させましたが、「サイクルが乱れないことの証明」はありません。なくても良いと思っていたのですが、気にはなっていました。その後、時間が出来たので、少し考えていると、「やはり、この点までも証明しなければならない」と思うようになり、漕ぎ出したのが ver21 以下の証明です。

ver20　の証明は有効であり、そこで検討した事例の大半については証明終わりです。残っているのは、サイクルを使った証明だけであり、それをver21以下で取り上げるということです。証明対象のk(s)の形はひどく奇妙なものですが、証明としては、ここにも矛盾が生じることを示さなければなりません。考えやすい形はすべてver20で証明されているとご了解ください。

ver30　あたりまでは kv(s)　を極座標回転させて、そこに矛盾を見つけるという方針でしたが、どうやっても矛盾になりません。矛盾にならないどころか、矛盾が無いことの証明まで出来そうな感じになってきました。これではいけません。やむなく kv(s)　を使う証明は諦めることにしました。

kv(s)以外の関数を検討したのですが、いろいろやっても、kv(s)と同じことでした。

そして、諦めかけていたとき、hk(s) = k(s)/k(s-0.5) という関数を見つけました。これは ver1 の証明に使った hk(x)　を修正したものです。kv(s)と零線図が異なるので、矛盾を見つけられるかもしれないと思いましたが、これも失敗でした。

そこで、さらに修正して　oe(s) = k(s)*k(a-0.5-b*i)　という関数を思いつきました。これは掛け算で　０＊０　となるので、hk(s) より証明がしやすくなります。これが ver36 の証明です。

oe(s)にも零線図があり、k(s)と同じ点が零点となります。もし、k(s)に横に並ぶ零点があるなら　（a=0.5外に零点がある場合、必ずペアで横に並んで存在します。これは証明済み。）　oe(s)　にも同じ場所に零点が存在することになります。横に並ぶと言うことは、k(s)をその距離だけずらして掛け合わせると、０＊０となる点が発生します。ｍをその距離として、oe_m(s) = k(s)*k(a-m-b*i)　と定義します。ｍは０から０．５までのどの値でもとれるとも考えられます。そして、０から連続して変化するときの oe_m(s)　の零線図を検討すると、０＊０が発生する瞬間、すべての事例において矛盾となることが確認できます。

その矛盾をＬ矛盾と名づけます。これは、k(s)が(1,0)以外の点ですべて微分可能であると言うことを前提にしています。k(s)が微分可能なら、oe_m(s)も微分可能です。（これも証明できます。）ところが、oe_m(s)の０＊０の点は微分不可となります。これは矛盾と認定できるのではないでしょうか。

以上の説明である程度可能性を認められるなら、証明本体を見ていただければと思います。修正しながら出来上がっているので、ver36に辿り着くには表紙から入る必要があります。






証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部


＜第９部以下の証明は表紙から辿ってください＞




■　　　　　ver20 履歴

2010/05/18　　　２の９を修正。マイナス階乗公式はそのまま虚数に拡張できません。結構大きな修正なので大問題ですが、今は時間がないので注意を促すだけです。いずれ近いうちに修正します。
2010/07/03　　　先の「２の９を修正」を撤回します。以前のマイナス階乗公式はbプラスの場合、複素数まで問題なく拡張できるようです。問題があるのは実数階乗公式のほうで、これを複素数に拡張する際に問題が生じます。

2013/12/28　　　「１の１９」を追加しました。






表紙に戻る