リーマン仮説（リーマン予想）の証明
　　　　　　　　　　ver35.2

第１１部を参照したい人は、ページの最後にある目次をクリックしてください。


ver20では、ひとつの横Ｕ字形の内部にリーマン零点がふたつある場合を想定して、そういう事例が存在し得ないことを証明しました。ふたつの横Ｕ字形にまたがってリーマン零点が存在すると言うことは、零線図を見る限りはあり得ないように思えたので、初めは検討する必要を感じませんでした。しかし、証明ですから、取り上げないことは許されません。そこで、ver20の最後のところで、その証明に取り組みました。その結果、それまでの証明のやり方が通用しないことが判り、証明方法を変更せざるを得なくなりました。いろいろ探した結果、サイクル（周期）というやり方で矛盾をあぶり出すことが出来ました。それで ver20 を公表することになったわけです。

しかし、その後、サイクル（周期）を調べているうちに、「どうも不充分」と思える点が見つかりました。そこで、別の証明方法を探したのですが、結局、周期の矛盾に帰着するものばかりで、それを超える矛盾はなかなか見つかりませんでした。

現実のk(s)を見る限り、「ふたつの横Ｕ字形にまたがってリーマン零点が横に並ぶ場合」などあり得ないことは直感的に明白なのですが、証明となると、証明に相応しい論理が必要となります。ところがk(s)の場合、全体的に不規則な運動をする関数なので、証明の根拠となるものがほとんどありません。ver27では、極座標図に輪が現われるということが矛盾であることを証明し、これを根拠に証明を完成させようとしたのですが、これは見事失敗してしまいました。その他のやり方もトライしましたが、うまくいきませんでした。

そうこうしているうちに、ver29 になりました。ver29では、リーマン零点が現われる場所の極座標を回転させることにより、矛盾を抽出する方法を採っています。これはうまくいったと思ったのですが、これも最後に証明できない事例が出てきてしまい、壁にぶつかりました。

結局、このやり方を諦めて、一番最初に使ったhk(x)を修正したhk(s)を検討している中でver35の証明にたどり着きました。第１０部の証明方法の（Ｋ）（■１０の２１）で説明してあるのがver35の本体です。

不充分な点や間違いを見つけた方がおられるなら、ご指摘いただけると大変助かります。連絡先はＨＰの最後に書かれています。









第９部　　　　ふたつの横Ｕ字形が横に並び、そのそれぞれにリーマン零点が存在する場合





■９の１■　　　　　　事例の分類方法


「リーマン零点が横に並ぶ」という現象が、ひとつの横Ｕ字形の内部では起きないことは第６部で証明してあります。残っているのは、別の横Ｕ字形のそれぞれにあるリーマン零点が横に並ぶことです。その形では周期に矛盾が生じることを、第８部で証明しましたが、第８部の証明ではまだ不充分かもしれないので、新たに別の方向での証明を追加することにしました。まずは全体的な説明をした上で、個別に矛盾点を指摘し、証明してゆくことにします。

そこで、第９部として、ふたつの横Ｕ字形が並ぶ事例を分類することします。第６部で証明し残したものも含まれます。「ふたつの横Ｕ字形が並ぶ」とは、横Ｕ字形のそれぞれにリーマン零点が存在し、それらが a=0.5 から等距離のところに横に並ぶということです。リーマン零点が横に並ぶと、横Ｕ字形も横に並ぶことになりますが、その並び方はいろいろあったとしても、無限に可能なのではありません。実零線の形としては、横Ｕ字形がふたつ並ぶ場合と、入れ子になっている場合の２種類しかありません。（実零線同士が交差する場合は、極座標の回転のひとつとして分析することになります。）そして、それぞれのどこにリーマン零点があるかというと、実零線・虚零線の角度が問題なので、横Ｕ字形の下側と中央と上側の３つを検討すれば充分です。また、その零点を虚零線が通過するのですが、虚零線の形の可能性も有限です。これらの組み合わせで、すべての事例をカバーすることができます。



■９の２■　　　　　　実零線による分類




検討対象の場所に４本の実零線があります。それらの組み合わせは、以下の通りです。

（１）実零線第１と第２が繋がり、第３と第４が繋がる場合。
（２）実零線第１と第４が繋がり、第２と第３が繋がる場合。

第１と第３が繋がると、実零線の交差が発生しますが、これは極座標回転により現われる図と同じなので、事例分類からは省きます。

結局、実零線についてはふたつの種類があることになります。







■９の３■　　　　　　リーマン零点の場所による分類




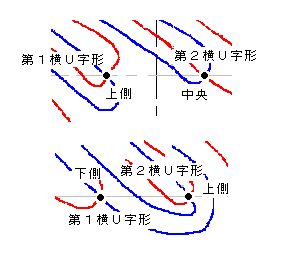
実零線は常に横Ｕ字形として存在するので、その線の下側、中央、上側の３カ所にリーマン零点が現われる可能性があります。左端の実零線から始まる横Ｕ字形を第１横Ｕ字形、それ以外の横Ｕ字形を第２横Ｕ字形と呼ぶことにします。



（１）　　　実零線の第１横Ｕ字形の下側と、第２横Ｕ字形の下側にリーマン零点があるとき。

（２）　　　第１の下側と第２の中央にリーマン零点があるとき。

（３）　　　第１の下側と第２の上側にリーマン零点があるとき。

（４）　　　第１の中央と第２の下側にリーマン零点があるとき。

（５）　　　第１の中央と第２の中央にリーマン零点があるとき。

（６）　　　第１の中央と第２の上側にリーマン零点があるとき。

（７）　　　第１の上側と第２の下側にリーマン零点があるとき。

（８）　　　第１の上側と第２の中央にリーマン零点があるとき。

（９）　　　第１の上側と第２の上側にリーマン零点があるとき。







■９の４■　　　　　　虚零線による分類




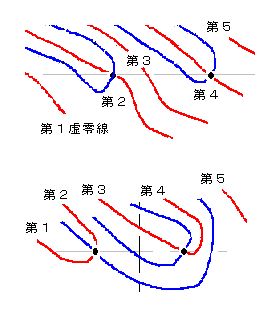
虚零線で検討対象になるのは５本です。左から（下から）１番、２番と番号を付けます。横一本線と横Ｕ字形のすべての組み合わせは以下の通りです。

（１）すべてが横１本線のとき。

（２）第１と第２が繋がり、残りが横一本線のとき。

（３）第２と第３が繋がり、残りが横一本線のとき。

（４）第３と第４が繋がり、残りが横一本線のとき。

（５）第４と第５が繋がり、残りが横１本線のとき。

（６）第１と第２、第３と第４が繋がり、第５が横１本線のとき。

（７）第１と第２、第４と第５が繋がり、第３が横一本線のとき。

（８）第１と第３、第２と第４が繋がり、第５が横一本線のとき。

（９）第１と第３、第４と第５が繋がり、第２が横一本線のとき。

（１０）第１と第４、第２と第３が繋がり、第５が横１本線のとき。

（１１）第１と第４、第２と第５が繋がり、第３が横１本線のとき。

（１２）第１と第４、第３と第５が繋がり、第２が横１本線のとき。

（１３）第１と第５、第２と第３が繋がり、第４が横１本線のとき。

（１４）第１と第５、第２と第４が繋がり、第３が横１本線のとき。

（１５）第１と第５、第３と第４が繋がり、第２が横１本線のとき。

（１６）第２と第３、第４と第５が繋がり、第１が横１本線のとき。

（１７）第２と第４、第３と第５が繋がり、第１が横１本線のとき。

（１８）第２と第５、第３と第４が繋がり、第１が横１本線のとき。




以上の組み合わせですべての場合を網羅していると言えます。事例（１，５，２）、事例（２，３，１０）のように表示して、まず実虚零線図の形を特定して、それから分析を始めます。中には初めから作図不可能なものもあります。それはその都度指摘することにしますので、ご了解ください




■９の５■　　　　　　矛盾の種類


それぞれの形ごとに相異なる矛盾が生じますが、その矛盾の種類は以下の通りです。個別分析では、その事例がどの矛盾に当たるかが検討されます。それぞれの矛盾の説明と証明は、第１０部以降を参照してください。



（Ａ）同一線上にふたつのリーマン零点が発生する。

（Ｂ）ふたつのリーマン零点以外に、もうひとつのリーマン零点が単独で発生する。

（Ｃ）実零線どうし、虚零線どうしが交差する。（廃止・修正）

（Ｄ）a=0.5の縦の極座標で、角度増加が起きる。

（Ｅ）kv(s)のｒθ図において、a=0.5付近で下向きの湾曲が生じる。（不使用）

（Ｆ）a=0.5付近に輪が発生する。（不使用）

（Ｇ）a=0.5以外の縦方向での角度矛盾（不使用）

（Ｈ）反転して重ねると矛盾が生じる。（不使用）

（Ｊ）k(s)をθ度回転させると矛盾が生じる。

（Ｋ）hk(s)を使った証明　　　　new 13/02/18


このうち、ＥからＨまでは、それ自体の証明が失敗したとか、論理が重複するなどの理由で、証明の根拠として使うことを諦めました。結局、ＤとＪとＫを使った証明となります。









第１０部　　　証明の根拠となる矛盾の種類



■１０の１■　　　　　　（Ａ）、（Ｂ）の矛盾


（Ａ）同一線上にふたつのリーマン零点が発生する。

（Ｂ）ふたつのリーマン零点以外に、もうひとつのリーマン零点が単独で発生する。


ＡとＢは第６部で使った矛盾で、すでに証明済みです。詳しくは第６部を参照してください。ここでは概略を説明します。


同じ実零線上にふたつのリーマン零点があり、そこを一本の虚零線が通ると閉鎖空間が出来上がります。すると、実零線の微分零線と、虚零線の微分零線がこの閉鎖空間から外に出られないと言う矛盾が生じます。

また、２本の虚零線の場合、横Ｕ字形内部の無限点から１本しか虚零線が来てないので、ひとつが繋がる相手を見つけられず、途中で途切れてしまいます。これは矛盾です。

Ａについての厳密な証明は、第６部を参照してください。




（Ｂ）ふたつのリーマン零点以外に、もうひとつのリーマン零点が単独で発生する。

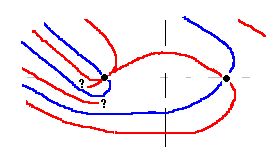
a=0.5以外にリーマン零点がある場合は、常にa=0.5から等距離の所にペアで存在します。これについては、第２部で証明済みです。ですから、リーマン零点が単独で発生することは矛盾と認定されます。これについては、第２部を参照してください。


右図において、？１の場所はＡ矛盾であり、？２の場所は、すでにリーマン零点がふたつ存在しているので、Ｂ矛盾となります。









■１０の２■　　　　　　（Ｃ）実零線どうし、虚零線どうしが交差する場合。（修正）


この部分は途中までの証明は正しくて、あとで根拠として使うことになったので、修正して載せてあります。ver29とは結論部分は異なっているのでご注意ください。また、交差が矛盾であるとしているわけではありません。



実零線と虚零線は交差してリーマン零点を発生させます。k(s)の零線図を見る限り、実零線同士、虚零線同士は交差していません。（注　　　k(s)を極座標回転させると交差が発生することを発見しました。）しかし、他の複素関数では交差するケースもあります。これはどういうことでしょうか。k(s)にないとしても、他の関数にあるからには、交差を矛盾と考えるわけにはいきません。しかし、特殊なケースではあるので、どういう条件のもとで交差が起きるかを分析してみました。

ここで分析するのは、「零線図において交差する」ことです。ｘｙ座標やｒθ座標で交差しないのは当然のことです。また、極座標では、実零線・虚零線はないので、別問題となりますが、極座標の曲線はごく普通に交差しています。零線図ではどうなのかという問題であることにご留意ください。




■１０の３■　　　　　　微分係数はひとつだけ


さて、複素数 s=a+b*i の実部a と 虚部b は独立した数ではなく、あざなえる縄のように、相互に影響しあって存在しています。いわゆる「存在」といえるのは 複素数 s であって、a, b ではありません。それゆえ、a, b が決まると、その点における傾きが決まります。その傾きそのものが複素数であって、それが複素関数の微分係数という構造になっています。

この命題は、「微分係数決定の法則」と同じことで、ver20 ■５の１１■を参照していただきたいのですが、この命題そのものは証明無しに受け入れることにします。なぜなら、微分係数を計算する公式は発見されていて、このhirokuroの証明ではすべて公式と認められるものは証明なしに使うことが出来るからです。

ver 20 ■５の１１■の計算式を使ってみれば判りますが、微分係数を計算する式はあらゆる複素関数で誤差無しに成り立っています。シンプルな式ですから、この式の当否を議論する余地はありません。問題なく、証明の前提として使うことが出来ると考えますが、どうでしょうか。

まずは、複素点における傾きを計算する式を再掲します。s=a+b*i　として、aについての微分を　f '(s) = s1 = c+d*i 　とします。すると、t1 = e^(ln-re(s1)　であり、また、t1 = √(c^2+d^2)　でもあります。t2 = ln_im(s1)　であり、また、t2 = pi+atan(d/c)　でもあります。そして、微分係数は　実部が　t1*cos(θ+t2)　虚部は　t1*sin(θ+t2)　となっています。

つまり、ある任意の関数内の点pにおける傾き（微分係数）は複素数としてひとつに定まると言うことです。

さて、k(s)は複素関数なので、sが定まると傾きも定まります。そして、その傾きは上記の公式から、実部は　t1*cos(θ+t2)、虚部は　t1*sin(θ+t2)　となります。

実零線とは、実部が零と言うことで、その点の傾きはいろいろですが、実零線の接線の方向での傾きは必ず零になります。それゆえ、微分係数のt1*cos(θ+t2)=0 ということです。t1,t2はs1により定まっているので、θもひとつに定まります。

さて、もし、ここに別の実零線がこの点を通っていたとします。すると、一点（交点）を共有しているので、その点におけるk(s)の値はひとつですから、微分係数もひとつになります。つまり、別の実零線の微分係数実部を　t1'*cos(θ+t2')=0　、虚部を　t1'*sin(θ+t2')=0　とすると、この実部どうし、虚部同士が等しいと言うことです。角度が異なっても等しいのですから、それは t1=0 ということです。微分係数実部零、虚部零と言うことです。つまり、この点はすべての角度において傾き零、つまり、平らであるということになります。

虚零線どうしが交わる場合も同じことです。虚零線が交わるとは、別の角度で交差していると言うことですが、その交点においては微分係数決定の法則が成り立ち、すべての角度に於いて　t1*cos(θ+t2)　となっています。相異なる角度でもひとつの値を取るとは、t1=0 以外にありません。ゆえに、ここは微分零点であり、θに関係なく、あらゆる場合で微分零、つまり、平らな場所となります。

これはとても重要なことで、k(s)を極座標回転させても、微分零点の場所に変化・移動はありません。丁度、零点が動かないように、微分零点も極座標回転に対しては不動であるということは覚えておく価値があります。




■１０の４■　　　　　　（Ｄ）a=0.5の極座標で、角度増加が起きる矛盾。



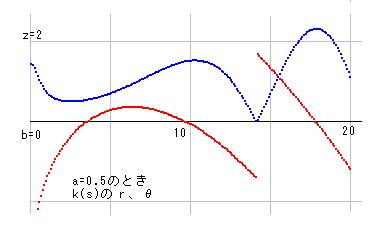
k(s)はkv(s)と異なり、不規則に動く関数なので、一般に k(s) の計算式を証明の根拠として使うことは出来ません。しかし、a=0.5 の角度は kv(s) と完全に連動するので、綺麗に公式化することができます。ゆえに、この公式を根拠に矛盾を認定することが出来ます。

k(s)の角度公式を　k_th(s)　で表すと、kv_th(s) ≡ - 2 * k_th(s) という関係にあります。これは恒等式で、b=0 からこの等式が成り立ちます。

たとえば、s=(0.5,10) の点に於ける角度は、k_th(s) = -7.4518257E-2 、kv_th(s) = 1.4903651E-1 で、kv_th(s) = -2*k_th(s) が成り立ちます。また、s=(0.5,15) の点では、k_th(s) = 1.3650113, kv_th(s) = -2.7300226 となり、等式は成り立ちます。ただし、角度の場合は補正が必要なこともあるので注意が必要です。角度は右廻りと左廻りで、値は異なりますが、同じ角度を意味しています。つまり、1.0 の角度と、7.283185 ( 7.283185-2pi = 1.0 ) の角度は同じなのです。また、-5.283185 ( -5.283185+2pi = 1.0 )　も同じ角度です。2*pi で一回りするからです。

また、atan(b/a) を使って角度計算するとき、プラスとマイナスが逆になることがあります。これは補正とは別の問題ですが、計算式ではフォローできないので、各自で訂正するしかありません。

kv_th(s) ≡ - 2 * k_th(s)　の式は、kv(s) = k(1-s)/k(s) という定義式から導けます。

k_re(1-s)=k_re(s), k_im(1-s)=-k_im(s)　なので、atan(k_im(1-s)/k_re(1-s)) = -atan(k_im(s)/k_re(s))　となります。ゆえに、極座標角度は　k_th(1-s) = -k_th(s) となり、kv(s) = k(1-s)/k(s) なので、角度は引き算になり、kv_th(s) = k_th(1-s) - k_th(s) = -2*k_th(s) となります。



この式を踏まえて、まず、kv_th(s)を求め、kv_th(s)が常に増加であることを証明し、次に、k_th(s)の角度が常に減少することを証明します。

kv_th(s) は、kv(s)の定義式を細分化して、個別に分析して、最後に総合して求めます。kv(s)を分析するためには以下の式を使います。




■１０の５■

省略





■１０の６■　　　　　　a=0.5 の kv(s)の角度公式



kv(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s }　という公式はリーマン仮説証明で非常に重要な役割を果たしています。これを使って角度公式を求めます。ただ、このままだと分析しにくいので、以下のようにこの式をさらに細分化して、最後に合計することにします。

s! = (s/e)^s * √(2pi*s) * e^mo(s)　これは実数階乗の公式を複素数になおしたものですが、bがプラスのときに成り立ちます。(s/e)^sの分母を全体の分母に移します。すると、kv(s) = s^s * √(2pi*s) * e^mo(s) * 2cos(pi*s/2) / { s * (2pi*e)^s }　となります。

s=a+b*i　とすると　s^s = s^a * (cos(b*ln(s))+i*sin(b*ln(s)))　なので、

kv(s) = s^a * (cos(b*ln(s))+i*sin(b*ln(s))) * √(2pi*s) * e^mo(s) * 2cos(pi*s/2) / { s * (2pi*e)^s }　

となります。


右辺を５つの式に分割します。

f01(s) = s^a * √(2pi*s) / s

f02(s) = cos(b*ln(s))+i*sin(b*ln(s))

f03(s) = e^mo(s)

f04(s) = 2cos(pi*s/2)

f05(s) = (2pi*e)^s

と名付けておきます。kv(s) = f01(s) * f02(s) * f03(s) * f04(s) / f05(s) 　ということです。

角度については、kv_th(s) = f01_th(s) + f02_th(s) + f03_th(s) + f04_th(s) - f05_th(s)　となります。



■１０の７■　　　　　　f01(s) = s^a * √(2pi*s) / s

s^a=(a+b*i)^a　です。(a+b*i)を極座標表示に直すと　√(a^2+b^2)*(cos(θ)+i*sin(θ))　となります。θ=atan(b/a)　です。

ですから、(a+b*i)^aの極座標表示は　(a^2+b^2)^(a/2) * (cos(θ*a)+i*sin(θ*a))　となります。

√(2pi*s) / s = √(2pi/s)　、√(2pi)は角度には影響を与えないので無視します。1/√(s) の　√s　の極座標を計算します。すると、(a^2+b^2)^0.25 * (cos(θ/2) + i* sin(θ/2))　となります。

割り算は角度では引き算なので、f01_th(s) = atan(b/a)*(a-1/2)　となります。a=0.5　ということなので、f01_th(s) = 0　となります。



■１０の８■　　　　　　f02(s) = cos(b*ln(s))+i*sin(b*ln(s))


f02(s)　の角度は　a=0.5のとき、b*ln(b) + 1/8/b - 1/64/b^3 + 1/384/b^5 - ...　と並びます。

つまり、f02_th(s) = b*ln(b) + 1/2^2/2b - 1/2^4/4b^3 + 1/2^6/6b^5 - 1/2^8/8b^7 + ....　となります。f02_th(s) = b*ln(b) + Σ_[r=2,r=r+2] 1/2^r/r/b^(r-1)　と一般化できます。





■１０の９■　　　　　　f03(s) = e^mo(s)


mo(s)=B(2)/2s + B(4)/12s^3 + B(6)/30s^5 + B(8)/56s^7 + . . . 　と定義されています。

つまり、mo(s) = Σ_[r=2,r=r+2] B(r)/r(r-1)/s^(r-1)

e^mo(s) = 1 + 1/12n + 1/288n^2 + . . .　ということで、スターリングの公式に登場する式になります。


e^mo(s)の角度は以下の式で計算できます。

f03_th(s) = Σ_[n=2, n=n+2] { (-1)^(n/2)/b^(n-1) * Σ_[r=2, r=r+2] B(r)*(n-2)!*a^(n-r)/(n-r)!/r! }

a=0.5 として、判りやすく書くと、

f03_th(s) = - 1/b * { B(2)*0!/2^0/0!/2! }
　　　　+ 1/b^3 * { B(2)*2!/2^2/2!/2! + B(4)*2!/2^0/0!/4! }
　　　　- 1/b^5 * { B(2)*4!/2^4/4!/2! + B(4)*4!/2^2/2!/4! + B(6)*4!/2^0/0!/6! }
　　　　+ 1/b^7 * { B(2)*6!/2^6/6!/2! + B(4)*6!/2^4/4!/4! + B(6)*6!/2^2/2!/6! + B(8)*6!/2^0/0!/8! }
以下略





■１０の１０■　　　　　　f04(s) = 2cos(pi*s/2)

f04_th(s) = -pi/4 + 1/P - 1/3P^3 + 1/5P^5 - 1/7P^7 + . . .

P=e^(b*pi)



■１０の１１■　　　　　　f05(s) = (2pi*e)^s


f05_th(s) = b*ln(2pi*e)　　　（注　aに係わらず同じ式）




■１０の１２■　　　　　　結論




角度は足し算になるので、　kv_th(s) = f01_th(s) + f02_th(s) + f03_th(s) + f04_th(s) - f05_th(s)　　となります。

f01_th(s) = 0

f02_th(s) = b*ln(b) + 1/2^2/2b - 1/2^4/4b^3 + 1/2^6/6b^5 - 1/2^8/8b^7 + ....

f03_th(s) = Σ_[n=2, n=n+2] { (-1)^(n/2)/b^(n-1) * Σ_[r=2, r=r+2] B(r)*(n-2)!*a^(n-r)/(n-r)!/r! }

f04_th(s) = - pi/4 + 1/P - 1/3P^3 + 1/5P^5 - 1/7P^7 + . . . . .
P = e^(b*pi)　です。

f05_th(s) = b*ln(2pi*e)　　



■１０の１３■　　　　　　kv_th(s)が常に増加（ｂ方向でということ）であることの証明


以上の式を使って、kv_th(s) が b=10 以上において、増加関数であることを以下のように証明します。

常に増加とは、微分式が常にプラスと言うことです。ゆえに、kv_th(s) をbについて微分します。すると、

f01_th'(s) = 0

f02_th'(s) = ln(b) + 1 - 1/2^2/2b^2 + 3/2^4/4b^4 - 5/2^6/6b^6 + 7/2^8/8b^8 - ...　

f03_th'(s) = Σ_[n=2, n=n+2] { -(n-1)/b^n * Σ_[r=2, r=r+2] B(r)*(n-2)!/2^(n-r)/(n-r)!/r! }

f04_th'(s) = - pi/P * { 1 - 1/P^2 + 1/P^4 - 1/P^6 . . . } = -pi*P/(P^2+1)

f05_th'(s) = ln(2pi*e) = 2.837877067　　



f02_th'(s)のマイナス部分を合計すると、- 1/2^2/2b^2 - 5/2^6/6b^6 - 9/2^10/10b^20 -. . . となるので、b=1 のときの値は　-0.13895 で、ｂが増えると値は 0 に近づきます。横に並ぶリーマン零点は b=6　以下にないことは、有限の範囲なので実虚零線図から証明できます。ゆえに、マイナスの数として考慮するのは　b=6 のときの -0.00348 となります。

f03_th'(s) = 1/12b^2 - 13/240b^4 + 37/4032b^6 - 3/256b^8 . . で、ｂが増えると０に近づきますが、プラス方向からの接近なので、マイナス数としては考慮する必要はありません。



f04_th'(s)　は　b=6 とすると、-pi/2/e^(b*pi) = -1.023E-8 で、0と見なして問題ありません。

f05_th'(s)はプラスですが、割り算なので、2.837877067 がマイナスされます。


プラス要因は、ln(b)+1 以外にもありますがこれが最大増加要因なので、これを代表として使って、ln(b)+1-2.84-0.00348 >0 を解いてみると、　b > 6.275 となります。ゆえに、ｂが７以上のとき、kv_th(s)の傾きがプラスになることが証明できました。


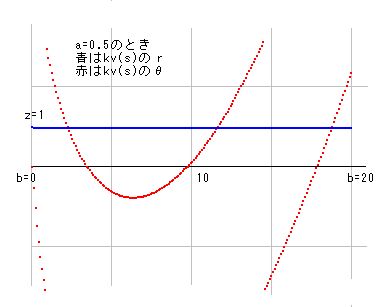
これはkv(s)の角度図を見ても明らかです。b=6.3あたりから増加に転じています。

ｂが７以下のところにはリーマン零点がないので、以下の議論の対象から外されています。

この部分にリーマン零点が無いことは実虚零線図から明らかです。図を使う証明はよろしく無いという考え方もあるでしょうが、ｂ < ７　は有限な範囲であり、すべて計算可能なので、証明として受け入れて良いと考えますが、どうでしょうか。





■１０の１４■　　　　　　k(s)の角度は常に減少



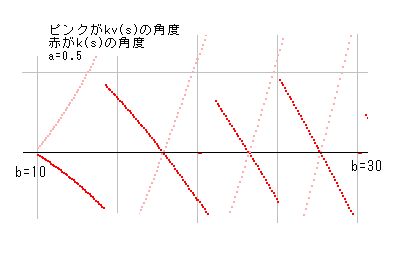
kv_th(s)が常に増加なので、k_th(s)は常に減少となります。これについては、すでに証明した　kv_th(s) = k_th(1-s)-k_th(s) = -2*k_th(s) という公式を示すことで充分でしょう。（参照　■１０の４■）　k(s)の角度はkv(s)の２分の１の速度で減少します。しかし、リーマン零点を通過することにより、半分の距離を端折るので、結果的に kv(s) と同じ速度で回転することになります。






■１０の１５■　　　　　　k(s)を回転させても　a=0.5 の角度は常に減少。


Ｊ矛盾のところで k(s) の回転について取り上げますが、そこでも a=0.5 において角度は常に減少します。その理由は以下の通りです。

k(s)の角度を変えると言うことは、極座標のθの値を変えることを意味しています。θにθ1を加えると理解するなら、θ1=0 というのが先に挙げた角度公式となります。角度にθ1を加えた式は　y+θ1=f(x) ということなので、先の式をθ1だけ上に移動させた図になります。つまり、θの図と合同ということです。そして、先の式が常に減少と言うことですから、k(s)を回転させた図、つまり、角度を変化させた図においても、角度（ｙの値）は常に減少ということになります。


（Ｅ）、（Ｆ）、（Ｇ）、（Ｈ）は不適切だったり、同じ論理、もしくは、不充分のようなので、省略します。






■１０の１６■　　　　　　（Ｊ）　k(s)をθ度回転させると生じる矛盾（極座標の回転）


複素関数はすべて極座標で考えることが出来ます。極座標とは、長さｒと角度θで表現する座標で、角度とはｘ軸（角度０軸）からの角度を意味します。x = r*cosθ, y = r*sinθ という関係にあります。このθを増やすとｘｙ座標図も実虚零線図も変化しますが、極座標図ではその角度だけ回転した図が得られます。それゆえ、角度を変化させることを「回転させる」と表現することにします。


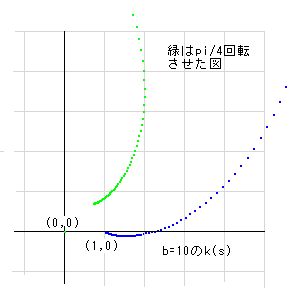
すべての複素関数は角度を変えると、その変えた分だけ回転します。たとえば、k(s)で、b=10のとき、横方向に切った極座標図で、角度にpi/4 加えて作図すると右のようになります。丁度、pi/4 度回転していることを確認できます。
















縦に切っても同じことです。a=0.5 として、同じように　pi/4 加えて見ることにします。すると、右図のようになります。












k(s)を回転させると、ｘｙ座標図も実虚零線図も変化しますが、回転するわけではありません。次の図のような動きになります。ただし、リーマン零点の場所は変わりません。なぜなら、x = r*cosθ, y = r*sinθ　で、リーマン零点とは　r=0　ということなので、θが変化しても零であることに変わりないからです。


ｘｙ座標で a=0.5 として、θ=pi/8 を加えてみます。すると、右図のようになります。リーマン零点の場所が同じであることは確認できます。また、pi/8程度の変化なので、前のk(s)と大差の無い形になっています。










pi/4　回転させると変化が広がります。















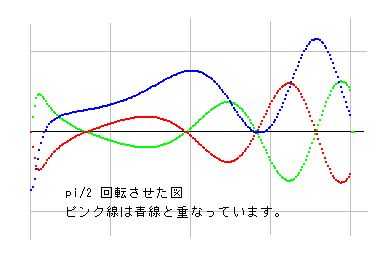
pi/2 回転させると、虚部線が前の実部のところに来て、実部線は前の虚部線とマイナスを介して一致します。

















3pi/4　回転させると、さらに変化し、pi 回転させると、上下逆の図が出来上がります。

piを超えると、前の図に戻り始め、2*pi で元に戻ります。

つまり、無限に変化するのでなく、2*piの範囲で一定の幅の間を波のように運動することになります。






a=0.5でなくても同じことです。a=0.7 のとき、pi/8, pi/4, . . . と変化させた図を重ねると右図のようになります。

















■１０の１７■　　　　　　零線図の変化





実虚零線図も似たような動きになります。零点はプラス・マイナスがないので、2*pi ではなく、pi で一巡します。

右図は　pi/4 回転させたときの零線図です。pi/2 で実零線と虚零線が入れ替わった図になり、pi で元に戻ります。

0, pi, 2pi, . . . 　のときは、実零線は横Ｕ字形となり、虚零線の多くは横一本線となります。pi/2, 3pi/2, 5pi/2, . . . 　のときは、虚零線が横Ｕ字形となり、実零線の多くは横一本線となります。それ以外のときはすべて実零線も、虚零線も横Ｕ字形となります。

横Ｕ字形となることの証明は、a=∞　において、k(s)=(1.0)　なので、r=1, θ=0 と確定しています。このときの角度を変化させるとは、θ=0.1 などのように数値を入れることです。この場合、数値が 0, pi/2, pi, 3pi/2, . . . でなければ　cosθ、sinθは零になりません。cosθ、sinθが零でないと、x=r*cosθ,　y=r*sinθ　, r=1　なので、x, y も零になりません。ゆえに、a=∞点を実零線、虚零線が通ることはなく、a=0　を通過した実零線、虚零線は、必ずどこかで別の実零線、虚零線と繋がり、横Ｕ字形となります。



角度が０からpi/2までの間のときは、虚零線の横Ｕ字形は必ず実零線の横Ｕ字形の下に来ます。pi/2からpiまでは虚零線の横Ｕ字形が実零線の横Ｕ字形の上に来ます。




さて、リーマン零点が横に並んで存在すると仮定すると、k(s)の回転図に矛盾が生じます。その矛盾とは、実零線、虚零線の横Ｕ字形の繋がる相手がなくなる矛盾（Ｊ１タイプ）、a=0.5の縦線上で角度増加が起きる矛盾（Ｊ２タイプ）、それに、リーマン零点上で、実零線、虚零線の繋がりが混乱する矛盾（Ｊ３タイプ）、虚零線同士が接触した後、分離し、尖った形になる矛盾（Ｊ４）があります。個別事例分析の中で、どのタイプの矛盾かを明らかにしますが、複数の矛盾を持つことも多々ありますので、その内のどれかを指摘しただけで終わらせることもあります。証明としてはそれで充分だからです。その点はご了解ください。

（Ｊ１、Ｊ３、Ｊ４タイプは廃止。結局、ver35で使うのはＪ２矛盾だけです。）






■１０の１８■以降は ver36 では撤回されています。ver36 を辿る方は次の「第１０部後半」へと進んでください。





■１０の１８■　　　　　　矛盾の具体例　Ｊ２矛盾


Ｊ矛盾をどのように指摘するかを示してみます。

Ｄ矛盾の場合は、最初から角度増加が起きていますが、角度増加の無い事例もたくさんあります。その場合、極座標図を回転させると角度増加が起きることがあります。



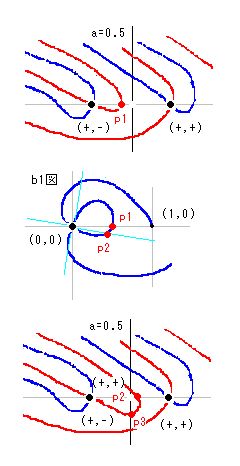
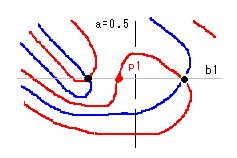
事例（１，４，１０）を使って、どのように角度増加が起きるかを示してみます。

ふたつのリーマン零点はa=0.5から等距離のところで横に並んでいます。そのときのｂの値をｂ１とします。ｂ１上（ｂの横線）の極座標図を描いたのがｂ１図です。（１，４，１０）の場合、ふたつのリーマン零点の間に虚零線が走っています。この虚零線とｂ１との交点をｐ１とします。このとき、a=0.5上では角度増加は起きていません。（証明できないという意味）

そこで、極座標を左に回転させた図を作ります。左にθ1回転させたいときはθ+θ1を新しい角度、絶対値ｒは同じで、x=r*cos(θ+θ1), y=r*sin(θ+θ1)　で求められます。作図の都合で極座標軸（シアン線）を右に回転させた図を載せておきますが、極座標図は相対的に左に回転していると考えてください。軸の名前は、角度０軸、pi/2軸、pi軸、-pi/2軸で、2piで元に戻ります。

左回転に従って、シアン線との交点はｐ２に移動します。さらに回転させると、リーマン零点である (0,0) に近づきます。

これを次の零線図で考えると、回転に従って、ｐ１にあった交点が右リーマン零点に近づきます。その途中で必ずa=0.5の線を越えることになります。






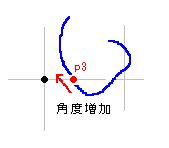
このときのa=0.5上の角度を考えると、(+,-)から(+,+)へと移行する部分が発生します。k(s)を回転させても a=0.5上の角度は減少であることは　■１０の１５■　で証明されているので、角度増加は矛盾と認定できます。

ゆえに、このような矛盾する作図を許す（１，４，１０）は実際に起きることはありません。






■１０の１９■　　　　　　Ｊ３（矛盾）


（Ｊ３矛盾は矛盾の起きないように作図することが可能なので、一旦は削除しましたが、ver35.2の証明で、これと関連のある論理を使うことになったので復活させます。文章は一部変更することにしました。）


Ｄ矛盾（角度増加）を指摘できない事例もあります。その場合は、回転させてもリーマン零点が動かないことを利用して、実零線と虚零線の交差・接触から矛盾を指摘できます。これをＪ３矛盾と名付けておきます。


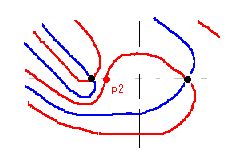
事例（２，６，６）を使ってＪ３矛盾を説明します。

（２，６，６）は実零線が入れ子状態になっていて、実零線第１横Ｕ字形の中央、第２横Ｕ字形の上側にリーマン零点があり、第１、第２虚零線が繋がり、第３，第４虚零線が繋がっています。





このときのｂ１極座標図は、右図のようになります。無限点は (1,0) なので、そこを出発すると、最初に交わる点が右側のリーマン零点です。次に虚零線と交わり（ｐ１）、次に左のリーマン零点、次に虚零線、実零線、虚零線と続きます。

どの領域を通過しているかが非常に重要です。無限点は(1,0)ですが、その後は (+,+) 領域が続き、右リーマン零点で始めて領域が変わり (-,-)になります。次に (-,+), (+,-), (+,+)　と変化します。この領域変化の場所が虚零線・実零線との通過点となります。







これを、左回転させます。左回転とは、k(s)の極座標角度を増やすことを意味します。すると、極座標図の形は同じですが、増やした角度だけ左回転した形になります。それに対応した零線図を作ると、pi軸との交点が左リーマン零点に近づいているので、ｘｙ座標においても、p1点が p2に移動します。このときの新しいk(s)の実虚零線図は次のようになります。実際は、零線図全体が少し歪むのですが、作業が面倒なので、p2点だけをずらしておきました。あとは想像で補ってください。







極座標図をさらに回転させるとｐ２点はさらに左リーマン零点に近づきます。回転させてもリーマン零点は動かないので、やがては両者は合体ます。










この合体したときの零線図は作りにくいのですが、あえて、そのような図を描くと右のようになります。

実零線横Ｕ字形の内部に２本の虚零線が通ることになります。すると、その線と、外に残る虚零線を結ぶと実零線との交点が生じてしまい、Ｂ矛盾が発生します。結局、内部に入り込んだ虚零線は繋がる相手を失うという矛盾になります。

ただし、極座標図を変更すれば、合体を避けることが出来るので、Ｊ３矛盾そのものを直接証明に使うことはできません。極座標図に適度な歪みを与えると、合体を避けることができます。しかし、今度は次に述べるＪ４矛盾の問題にぶつかります。Ｊ４矛盾と名付けたものは、ver35では、矛盾ではないと判断されているので、もはや矛盾とは言えませんが、一応便宜上、ここでは先の命名どおりにＪ４矛盾と言う場合もあることをご了解ください。実際は、実零線・虚零線の交差という現象は起きていて、Ｊ４矛盾の現象も起きています。この説明を残す理由は、次のＫ矛盾を判定する際に、Ｊ４矛盾の現象を使うこともあるので、説明としては必要です。Ｊ４矛盾は矛盾ではないと言うことはご理解ください。








■１０の２０■　　　　　　Ｊ４（矛盾）

（Ｊ４矛盾は、矛盾ではなく、実際に起きる現象です。ですから、ver29の説明は間違っていました。しかし、Ｋ矛盾の前提としてＪ４矛盾の論理が必要です。矛盾と言うことではなく、現象の理解のためにこの項目は復活させることにしました。そのため、文章の一部を変更してあります。）



極座標図の描き方はいろいろ可能であり、場合によってはｐ１が左リーマン零点に到達しない図も可能です。たとえば、極座標図の丸みが大きいとき、ｐ１が左リーマン零点に到達する前に交点そのものが消滅してしまいます。

このような場合、ｐ１が消滅する前に必ずL1線上にｐ３，ｐ４が生まれます。その時の零線図を作図すると右のL1図のようになります。これがさらに回転してｐ３とｐ４が合体し、その次の瞬間、虚零線との交点が無くなります。このとき、虚零線が無くなったのではなく、交点が無くなったので、L3図のような零線図になっているはずです。

極座標がさらに回転すると、虚零線はもっと滑らかになり、自然な形になります。このような現象が起こるということは考えにくいことですが、実際に起きているので、とても驚かされます。













■１０の２１■　　　　　　（Ｋ）　hk(s)を使って矛盾をあぶり出す証明


hk(s) = k(s)/k(s-0.5)　と定義します。k(s-0.5)は、k(s)を 0.5 右にずらしたもので、k(s)と内容は同じです。自らを変化させて割ると言うことは、kv(s)=k(1-s)/k(s) と似ていますが、ｓの符号が同じままで割るので kv(s) のような綺麗な公式にはなりません。しかし、k(s)のリーマン零点で割った結果が特異点として残るので、かえって矛盾が生じやすくなっています。



まずは hk(s)の全体像を説明します。hk(s)も零線図を描くことが出来ます。その姿はk(s)とかなり異なります。

実零線は横Ｕ字形としてはどこにも現われません。虚零線はaプラス無限から繋がる横Ｕ字形として、もしくは輪として、現われます。b=0　は実部のみ値を持つ場所ですが、ゆえに、虚部は零と言うことで、ここも虚零線が走っています。この図には書き込んでいませんが、b=0上には赤い虚零線があると思っておいてください。

a=0.5とb=0上に青い点がいくつも見えますが、ゴミではありません。ここに実零線の輪があります。その輪の間を虚零線が通っています。これらはリーマン零点付近に出来た輪なので、すべて同じ構造をしています。








この輪を拡大すると綺麗な円になっていたので驚いたのですが、厳密に計算してみると、残念ながら完全な円ではなさそうです。しかし、とにかく、円に近い形が繰り返し現われているところは、実に見事であると思います。その拡大図のひとつを載せておきます。



ところで、第６部の証明で、実零線と虚零線で作られる閉鎖空間は存在しないことが証明されています。ところが、この図を見ると、実零線の輪という閉鎖空間の中を虚零線が通っています。これは矛盾そのものという印象を受けます。

しかし、ここの右側の交点はk(s-0.5)で割ったことにより出来た特異点であり、値は無限大です。ゆえに、この空間は閉鎖されておらず、微分零線がここを通ることが出来ます。



この輪の中にある微分線は特異点に集まっていて、そこから外に出ているので、矛盾は生じないと言う理屈です。

実際に計算した結果を図示したのが右図です。この図を見ると、矛盾がないことがよく判ります。

リーマン零点が横に並んで存在する場所があるなら、hk(s)では４つ並ぶことになります。その中のふたつは普通のリーマン零点であり、そのふたつの零点を両端とする輪があるとすると、それは閉鎖空間になるので、矛盾と認定できるという予想はすぐに思いつきます。

これは大いに使える論理だと思ってやってみたのですが、事例分析で示してあるように、それを使う事例図は現われませんでした。しかし、リーマン零点がa=0.5以外には存在しないことを理解するには、とても有力な論理であることには変わりありません。ver35の証明の中では登場しない論理なので、あえてここで紹介しておきます。




■１０の２２の１■　　　　　　hk_m(s)の定義


さて、hk(s)だけでは証明の材料が足りないので、hk_m(s)という関数を導入します。

hk_m(s) = k(s)/k(s-m)　

hk(s)の0.5をmに換えただけの関数ですが、これを使うことにより、hk(s)でうまくいかないところを乗り越えることが出来ます。

mはプラスの実数で、k(s)をどれだけずらすかを示しています。

m=0とは、ずらすことなく自らを割ることになるので、全複素空間で答えは (1,0)　となります。複素空間内を実部１の実部平面、虚部が０の虚部平面が漂っているとご理解ください。このふたつの平面は複素数としてはふたつの平面ではなく、ひとつの複素平面を意味しています。

mが僅かに値を持つと、複素空間内に、あるはっきりした形が現われます。まず、リーマン零点のところは(0,0)になり、わずかmだけずれたところに無限大の値を示す特異点が出現します。a = 0.5+m 上にも、b=0 上にも特異点が現われるので、大きな変化となります。しかし、その他の点では、すべて極小の変化でしかなく、複素平面がわずかに波打っているという姿になります。

ただし、値は小さいとは言え、プラス・マイナスの変化がはっきりと現われるので、それを確認しておきます。


m が極小であるとはいえ、その零線図は、基本的にはhk(s)と大差ありません。

m=0.1 として計算したものが右図です。実零線（青点）がないのは、この段階ではまだ小さいので標示できないということです。虚零線は現われますが、m=0のときが全画面０だったのが、プラスとマイナスに分かれるという変化ですから、値は極小です。















ｍが0.5になっても零線図としての変化は大きくありません。しかし、１を超えると新しい線が登場します。

m=1　のときは、理論上は新しい実零線が登場しているはずですが、(-∞,0)　に登場するので、図には標示されません。

m=1.1　のときは、b=0上のすでにある古い実零線と重なって、新しい実零線としての姿が見えてきません。

m=1.4くらいになると、ようやく実零線が横一本線として現われます。


m=2 のときの零線図は右図のようになります。

















m=3 になると、新しい虚零線も現われます。

















これをk(s)の零線図で考えてみます。k(s)の零線図を右にずらして、自らに重ねるときに交点が発生します。その交点は２種あります。実零線同士、虚零線同士という同種の交点、実零線と虚零線という異種の交点です。同種の交点をhk_m(s)の虚零線が通ります。異種の交点をhk_m(s)の実零線が通ります。

右図はk(s)の零線図ですが、この図をm=3ずらして重ねてみると、出来た交点が、先に載せたhk_3(s)の零線図と重なります。自分でやってみてください。





m=0.5　ずらしても、すでにｍ極小のとき発生している交点が動いただけで、新しい交点は発生していません。しかし、証明としては、見た結果を根拠として使うことはできないので、交点はあらゆぶ場所で発生する可能性を排除しないで証明を進めることになります。









■１０の２２の２■　　　　ｍが極小のとき、実零線の輪が出来ることの証明

ｍが極小の時、実零線の輪がふたつ出来ます。これはリーマン証明 ver35 で使う基本的命題なので、ここで証明しておきます。

m=0　のとき、hk_m(s)は全画面で(1,0)となります。ｍが極小とは、(1,0)からの連続した変化により出来上がることを意味します。連続と言うことは、実部については１付近、虚部については０付近の値を取ると言うことです。ただし、特異点は例外です。特異点の場所を確認すると、k(s)の零点で割ったところなので、a=0.5上と、b=0上に発生することになります。

実部については、特異点以外は以外はすべて１付近と言うことなので、普通は零になることはありません。しかし、零点と特異点付近は別の動きになります。k(s)の零点はhk(s)でも零です。k(s-m)の零点が無限となって、特異点となります。この特異点は、ひとつの点で　+∞　と　-∞　の両方の値を持っています。その理由は、k(s)の零点の周辺の値がプラスとマイナスに分かれているからで、プラスから零に至るところでは、プラス無限となり、マイナスから零に至るところではマイナス無限となります。そして、特異点を境にプラスとマイナスが変化するので、その近傍に必ず実零線と虚零線が存在することになります。つまり、特異点そのものは零点ではありませんが、k(s)の場合、零点の頂点のような場所に特異点が発生するので、必ず実零線、虚零線が特異点を通るような形になります。これを、説明上、「実零線・虚零線が特異点を通る。」と表現することもありますので、ご了解ください。「実際は通っているのか？いないのか？」は、証明とは関係ない数理論上の問題となりますが、結構難しい問題だと思います。今後の検討課題としておきます。

零点も無限点も単独で存在するのでなく、周辺の(1,0)に近い値から連続した変化で零になり、無限にもなります。マイナス無限の場合、(1,0)からの変化の過程で必ず零点を通ります。ゆえに、無限点の近くにも必ず零点が発生します。また、マイナス無限の周辺はすべてマイナスですから、1,0)からマイナス領域への変化の過程で、その周辺には必ず零点となるところが発生し、それらの零点が繋がって輪になっています。そして、零点と特異点は　m=0 では同じ点であり、そこから連続した変化でマイナス部分の周辺に輪が発生しているので、零点とマイナス周辺とは必ず重なり、その輪は零点と特異点を含む輪として存在することになります。

もし、リーマン零点が横に並んでふたつ存在するという仮定で考えるなら、hk_m(s)には２つの零点、ふたつの特異点が存在することになります。そして、ｍは極小ですから、横にならぶリーマン零点の距離よりいくらでも小さい値を選ぶことは可能なので、極小のときは、零点と特異点のペアがふたつ存在することになります。そして、そのペアそれぞれに輪が存在することになるので、輪の数はふたつとなります。

最初からひとつの輪になることはありません。なぜなら、リーマン零点間の距離がいくら小さいとしても、ｍはいくらでも極小の値を取ることが可能で、ｍの変化が極小である限り、リーマン零点間の値は(1,0)から極小の変化でしかなく、零になることはできません。ゆえに、ここを零線が通ることはなく、零点とｍだけ右にずれたところに出来た特異点のペアはそれぞれ独立に輪になることになり、互いに繋がることは出来ません。


虚零線は、実零線と異なり、m=0　の時に零ですから、複素面のどこで零になっても矛盾ではなく、零線図はあらゆる形を取ることが可能です。ただし、k(s)/k(s-m)なので、零点と特異点は通過しなければなりません。また、b=∞　はk(s)の零点も無限点もなく、収束しないので、hk_m(s)も特定の値を取ることはなく、零点になることはありません。ゆえに、虚零線がb=∞に向かうことはありません。

残るは、a=+-∞とb=0ですが、この３つの方向への虚零線の接近はあり得ることとして分析することになります。ただし、ｍが極小のとき発生する虚零線はb=0上とaプラス無限から始まる左向きの横Ｕ字形、そして、輪になる形だけです。これはリーマン証明の中では使わないので、説明だけにしておきますが、「ｍが極小のとき、虚零線はa=-∞には向かわない（b=0以外）」ことの証明は今後の課題として残っています。






■１０の２３■　　　　　　Ｋ矛盾の分類



さて、仮定上のリーマン零点が存在するなら、hk_m(s)にも存在することになります。k(s)のｂ１上にふたつあるので、hk_m(s)には２つの零点と２つの特異点が存在することになります。特異点も実零線・虚零線が通るので、零線の通過点は４つとなります。

この場合、どのように証明を進めることになるでしょうか。証明の手順は複雑ですが、その複雑さに面白いところがあるので最初に解説しておきます。k(s)の事例図は合計（２＊９＊１８＝）３２４種ありますが、そのすべての事例でhk_m(s)の図を作って検討することになります。その際、ｍが何であれ、任意のｍに矛盾があるなら、その事例に矛盾があると認定されます。しかし、任意のｍに矛盾があると認定するためには、そのｍの事例図については、すべての可能性を検討しなければならず、ひとつでも矛盾が認定できないときは、そのｍに矛盾がないと判定されます。

たとえて言うと、本箱に３２４冊の（事例の数）本が並んでいます。ひとつの本はｍページ（無限）あります。それぞれのページには巨大なスペースがあって、そのスペースには白から灰色から黒までの模様が付いています。その一ページの中に一カ所でも白と判定されるところがあるなら、そのページ全体が白とみなされるというルールがあります。そして、一カ所も白がないページがあるなら、そのページは黒と判定されます。そして、一冊の本の中の無限のページの中で、一ページでも黒があるなら、その本全体は黒と判定されます。黒がなければ全体は白です。そして、本箱全体は、一冊でも白の本があったなら、本箱全体は白と判定されることになります。

このルールはリーマン零点証明と同じ構造です。白とは証明ができないことを示していて、黒とは矛盾があるということで、証明が完成することと対応しています。証明を完成させるには、事例のすべてが黒（矛盾がある）ことを示さなければなりません。そして、個々の事例については、任意のｍのひとつでも矛盾があると示せればよいのです。ただ、そのひとつのｍでの矛盾を示すためには、そこにある巨大なスペース（可能性）のすべてを検討し、そのスペースの中に矛盾のない箇所がひとつもないことを示さなければなりません。

スペースを事例図の空間と誤解するといけないので、もう少し正確な対応をするモデルで説明しますが、一ページの中が縦線と横線で区切られていて、その無数の区域ごとに様々な模様が出来上がっています。その区域の中に一カ所でも白という箇所があるなら、その区域全体は白と判定されます。そして、ひとつでも白と判定される区域があるとき、そのページ全体が白と判定されます。

さて、本箱全体は白なのでしょうか、黒なのでしょうか？というのがリーマン証明の課題で、黒であると言うことを言えれば、リーマン証明が完成したことになります。

そこで、証明を完成させるためには、各事例図のすべてに矛盾があることを示すことですが、そのためには、個々の事例図がｍ個の可能性をもっています。その中のひとつでも矛盾があると示せれば良いのですから、証明は簡単そうに見えます。しかし、ｍが極小のときは矛盾がないことは明らかですし、個々のｍの大部分は灰色であって、白と判定できるところはありますが、黒と判定できるｍはそう簡単に見つかりません。ですから、証明は大変なのです。



さて、話しを証明本体に戻しますが、ｍが極小のときは矛盾がありません。しかし、ｍを増加させると、やがて、実零線の輪が壊れてゆきます。このときの輪の壊れ方は各事例で異なるだけでなく、事例図の書き方によって様々ですので、そのすべての可能性をひとつひとつ取り上げることは面倒ですし、実際上不可能です。

そこで、ｍをさらに増加させたときの形を取り上げます。実零線の輪がどのような形で壊れたにせよ、また、壊れないにせよ、いずれは必ず隣の輪と繋がり、ひとつの輪となります。そして、さらにｍを増加させると、k(s-m)で割った特異点がk(s)のもうひとつの零点と重なるときが訪れます。この時、0/0が実行されるので、零点がなくなり、hk_m(s)の実零線・虚零線がここを通れなくなります。この時に矛盾が発生する可能性があります。

作図をしてみると、重なる直前も、重なった後も矛盾の無い場合が多いので、がっかりですが、直前から重なったときへの移行に矛盾が見つかることがあります。これはあとで説明するＫ２矛盾で、連続性が壊れる矛盾です。しかし、ここでも矛盾のないことがあります。その場合は、輪が接触したときの図、直前図、もしくは重なったときの図を用いて、その実虚零線図において、微分零線がどのように走るかを確認し、そこに矛盾を見いだすことになります。（Ｋ３矛盾）

一応、これですべての事例において矛盾を指摘できるようになったのですが、もし、これでも見つからない場合は、次の手段としては、k(s)を極座標回転させて、実零線・虚零線が組み替わる瞬間の図を用いて、hk_m(s)の図を作ることが可能です。これはまだアイデアだけで、実際に検討していませんが、もし、Ｋ３矛盾まで使っても証明が完成しないときは、このやり方もトライすることになるでしょう。

以下、Ｋ１、Ｋ２、Ｋ３、Ｋ４という矛盾を見つける手段を紹介します。それを使った具体例は事例分析の中で説明することになります。





■１０の２４■　　　　　　Ｋ１矛盾


さて、k(s)でリーマン零点がa=0.5上になく、横に並んでふたつ発生した場合、hk_m(s)にも、それに対応した場所にふたつのリーマン零点とふたつの特異点が発生することになります。

このような４つの点がある事例図であっても、ｍが極小なら、矛盾は発生しません。なぜなら、k(s)の零点とk(s-m)で発生する特異点の距離が極小なので、実零線の輪が２カ所発生し、それぞれの輪に特異点が含まれているので、矛盾を指摘できないからです。

ｍが少し増加すると、やがて最初のふたつの輪が壊れ、ひとつの輪になろうとします。このとき、うまく輪になれる場合と、輪になることに失敗する事例があります。

輪になることに成功した事例は、矛盾がありませんから、別の矛盾を探すことになります。しかし、輪になることに失敗した事例は矛盾と判定されます。なぜなら、輪にならないかぎり、実零線の繋がる先は見つからないからです。

輪にならずに、実零線が無限と繋がる可能性があるなら、矛盾とは認定できません。（注　　　実際は、無限と繋がることはなく、無限と繋がる事例もないので、この論理はこの証明では使いません。）

輪になることに失敗する事例とは、k(s)とk(s-m)の実虚零線が作る区域に奇数の緑点・桃点が存在する場合です。緑点とは、k(s)とk(s-m)の実零線と虚零線の交点で、hk_m(s)の実零線が通ります。桃点とは、実零線どうし、虚零線どうしの交点で、hk_m(s)の虚零線が通ります。この緑点、もしくは桃点が偶数ですと発生した零線どうしを繋ぐことができます。しかし、奇数では繋ぐことはできません。零線が途中で途切れてしまうのは矛盾です。このような矛盾が発生する場合をＫ１矛盾と名付けておきます。




■１０の２５■　　　　　　Ｋ２矛盾


ｍが連続なので、hk_m(s)の零線図も連続して変化しています。連続性が壊れるのは、特異点の場所だけです。ゆえに、特異点以外の場所で連続性が壊れているなら（飛躍があるなら）、それは矛盾として認定できます。これをＫ２矛盾と名付けておきます。





■１０の２６■　　　　　　Ｋ３矛盾


ｍが極小のときは実零線の輪がふたつ出来るだけで、矛盾はありません。しかし、ｍを増加させると、輪が大きくなり、隣の輪と接触し、やがては、ひとつの輪になる場合があります。その際、接触したタイミングでのhk_m(s)の実零線と虚零線の図を取り上げ、この時、aについての微分零線、bについての微分零線がどのように走るかを検討します。aについての微分零線は、実零線の上下の先端を通過します。虚零線の左右の先端を通過します。その上で、ふたつの輪の接触点は微分零点なので、ここも通過しなければなりません。また、特異点も通過します。これらの点をずべて通過できれば良いのですが、もし、通過できないとか、途中で途切れるなら、矛盾と判定されます。

ｂについても同じ作業が可能で、実零線の左右の先端と、虚零線の上下の先端を結んで、また、輪の接点の微分零点と特異点を通って、矛盾無く線を繋ぐことが出来るかどうかを検討します。もし、矛盾があるなら、これをＫ３矛盾と名付けます。





■１０の２７■　　　　　Ｋ４矛盾


k(s)を極座標回転させて、その図をhk_m(s)にすることが可能です。この事例に矛盾が発生することが指摘できると、k(s)にも矛盾が発生することになります。このやり方をＫ４矛盾と名付けておきます。

hk_m(s)を使う証明の場合、虚零線が１本線に繋がると証明が容易になることを発見しました。事例図が入れ子になる場合、このやり方でかなり手際よく証明が出来たので、入れ子にならない場合でも、極座標回転を使って、入れ子の図にして証明すればよいと思いつきました。

極座標を回転させると零線図の形に大きな変化が起こることはＪ３，Ｊ４で説明してあります。実零線・虚零線の組み替えが起こり、その繋がり方によっては入れ子の状態になります。入れ子になると、底が塞がれた状態なので、hk_m(s)の虚零線（桃線）が下に逃げることが出来ず、隣の輪と繋がります。すると、そこに狭い区域が発生するので、そこを通る微分零線の出口が塞がれ、矛盾を指摘しやすくなるという具合です。

もし、その区域に３本の微分零線が集まったとすると、それは互いに繋がることが出来ないので、矛盾となります。








ver20

証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部

以下、ver35

証明の第９部、第１０部

証明の第１１部

以下 ver36
証明の第１０部後半

証明の第１１部







■　　　　　ver35 履歴

(2013/03/14)　ver35.2 　　　Ｊ３、Ｊ４矛盾を修正して復活させました。



表紙に戻る



ご感想、ご質問、その他のご意見は、Mailのアドレス（bp5h-krs@asahi-net.or.jp）へお願いします。