リーマン仮説（リーマン予想）の証明

　　　　　　pn(s)、　 pp(s) による証明

ver51 　　　pn(s), pp(s)　による証明は失敗しました。














どこが失敗であったかは、あとの記事（１０の３８）の中で赤字で書き込んでありますので、興味のある方は参考にしてください。

どうやってもうまくいきませんね。ただ、この失敗で判ったことは、仮定上のリーマン零点を持つ関数には「ほとんど矛盾がない」ということです。「ほとんど」とは「絶対に」ではないので、今後も証明にトライすることは有益ですが、おそらく、仮定上の零点と同じ場所に零点を持つ関数　k'(s)　という関数を作ることは可能だろうと思います。実際に零点を持つ関数が存在しているのですから、矛盾が生じるわけがありません。ただし、その関数　k'(s)　と　k(s)　は似てはいますが、別の関数なのです。その別であることをどうやって証明するかが今後の課題となります。 　　　　　　2016/11/21













９部と１０部１節から２９節までは省略しました。事例分析も省略してあります。適宜、ver20, ver35　を参照してください。

今回の証明（ver51）は ver20　の続きという形になっています。ver35も一部前提にしてあります。アップしたのは証明の手順（論理）だけですが、この手順が正しければ、後日、証明の全体を整理して載せたいと思います。用語解説などは、ver20とver35を参照してください。






第１０部　　　証明の根拠となる矛盾の種類






■１０の３０■　　　　　　pn(s)　の定義


pn(s) = k(m-b*i) - k(s)

k(m-b*i)は、k(1-a-b*i)の変数 1-a を m という任意の定数で固定し、変数ｂはマイナスのままにしたものです。これからk(s)を引くとpn(s)になります。m は任意ですから、何でもよいのですが、今回の証明ではもっぱら m=0.5 のときを取り上げるので、この証明では m=0.5 と理解していただいて差し支えありません。

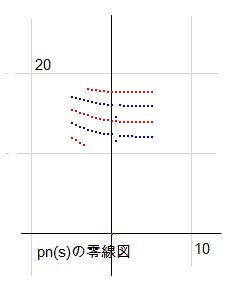pn(s)がどのような関数かは零線図を見るのが一番でしょう。m=0.5 として計算すると右図のようになります。a=0.5 の列に青点があるのは、縦に実零線が走っているからです。描かれてはいませんが、ここに実零線があると思ってください。

左上から緩やかに実零線と虚零線が交互に下ってきます。a=0.5あたりから平らになって、そのまま右に進みます。左半分については、kv(s)の零線図と極めてよく似ています。kv(s) = k(1-a-b*i) / k(s) なので、式の形もよく似ています。














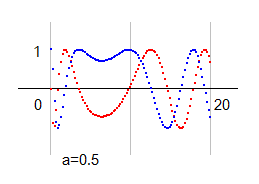
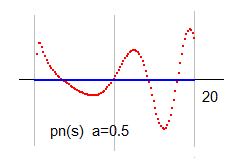縦に走る実零線を確認するために、a=0.5 の図を載せておきます。青線が実部波で、零に張り付いているのが判ります。赤線は虚部波です。

実部が零になることは　k(0.5-b*i) - k(s) から明らかです。a=0.5 のとき、実部は同じ値になるので、引き算すると零になるということです。虚部は逆の値になるので、２倍になります。







■１０の３１■　　　　　　pp(s)　の定義


pp(s) = k(m-b*i) / k(s)


pn(s)を割り算にするとpp(s)になります。m は任意の実数ですが、pn(s)と同じく、この証明では m=0.5 と理解します。

pp(s)がどういう関数かは、定義を見るとだいたいのところは判ります。pn(s)の引き算が割り算に変わっただけです。kv(s) = k(1-s) / k(s)　なので、kv(s)と関係があることはお判かりいただけると思います。




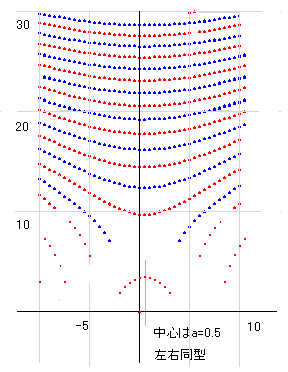まずは kv(s)　の零線図を再確認しておきます。ver20で、kv(s)に零点がないことが証明の出発点でしたが、最後に再登場になるとは不思議な巡り合わせです。

実零線と虚零線はどちらも、左上から下ってきて、a=0.5で底になり、また、右上に上る形になっています。実零線と虚零線は交互に現れていて、上に行くほど狭くなります。狭くなりかたは、k(s)と同じで、a=0.5の角度公式が見つかっているので、計算することができます。

a=0.5を軸に左右同型で、k(s)の零点の場所は、k(1-s)も零点なので、0/0 となり、普通の値をとるので零点はありません。零線図にも横Ｕ字形はなく、実零線と虚零線の交点はありません。











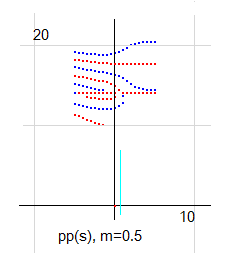pp(s)の零線図を見てみます。m=0.5 とすると、分子に零点があるので、横に実零線、虚零線が通ります。それ以外にも実零線、虚零線があり、右図のようになります。

リーマン零点を通る横線は、実零線（青線）と虚零線（赤線）の両方を意味しています。右図では赤線で表示されていますが、青線も通っているとご理解ください。












■１０の３２■　　　　　　pp(s)とkv(s)の一致点


pp(s)が証明の材料となるのは、kv(s)と一部一致するところがあるからです。ｍは定数ですが、aに　1-m　を代入すると kv(s) と pp(s) は同じ式になります。ですから、a=1-m の軸上の点はすべて一致することになります。

たとえば、m=0　とすると、a=1　の軸はすべて一致します。m=0.5　とすると、a=0.5 軸が一致します。式が同じなので、等しいことは一目瞭然です。

ただし、微妙なところがひとつあります。右図はkv(s)のa=0.5のbz図です。

pp(s)のa=0.5図もまったく同じ形になります。ところが、零線図を見ると、リーマン零点のところがpp(s)も零点になっているように見えます。計算上、ここは　0/0 なので、零点ではないのですが、周りから実零線、虚零線が集まってくるので、零点のように見えます。ところが、それは a=0.5 軸上のpp(s)の値には影響を与えません。驚かさせる現象ですが、こういうことがよくあるのが数学の現実です。あり得ないことが起きることがあるのです。ですから、厳密な証明が必要になるということです。







■１０の３３■　　　　　　仮定上の零点がある場合


さて、リーマン証明では、「k(s)のリーマン零点がa=0.5上以外にもある」　と仮定して矛盾をあぶり出すという証明方法（背理法）を使います。この仮定を「仮定上の零点」と言うことにします。仮定上の零点は a=0.5軸を挟んで左右両側に同じ距離にあります。等距離にあることはすでにver20で証明済みの命題です。このときのｂ軸の値をb1としておきます。

また、仮定上の零点は、ひとつの横Ｕ字形の線上にふたつ存在することが出来ないことはver20で証明済みです。閉鎖空間を作ることが出来ないからです。ver51では、ふたつの横Ｕ字形のそれぞれにリーマン零点がある場合を検討して、矛盾が生じることを示すことを目標にしています。

証明のためには、仮定上のリーマン零点がある場合の可能な零線図が必要になります。これは計算で描くことが出来ないので、手動で描くことになりますが、いろいろな形が可能なので、整理と分類が必要になります。そして、それぞれの事例ごとに分析しなければなりません。個々の事例分析は、それほど難しいことではありませんが、数が多いので時間がかかります。今回は、そのひとつを取り上げ、まずは証明手順を示して、そのやり方が正しいことを明らかにしてみようと思います。もし、この手順が本当に正しければ、後日、事例ごとの証明に入る予定です。

今回は、事例（１，３，６）を取り上げます。事例番号については ver35第９部を参照してください。ひとつの事例でうまくいけば全体もうまくいく可能性が生じますし、もし、ひとつで失敗するなら、全体を検証する意味はありません。







■１０の３４■　　　　　　事例（１，３，６）の pn(s)零線図を作る手順


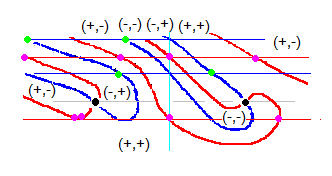事例（１，３，６）のpn(s)零線図は　仮定上のk(s)零線図を使って作ります。a=0.5 が基準軸なので、a=0.5 に水色線を引きます。水色線と青線、赤線の交点を通る、青横線、赤横線を引きます。仮定上の零線図ではリーマン零点はa=0.5上にありませんから横線は引きません。すでに灰色線が引かれているかもしれませんが、この線は無視します。

a, b, c, d を正の実数とします。青横線とは、a=0.5 軸上の実零線（実部零点）を通るので、その線上は (0,+-b) となります。青線はk(s)の実部零点なので (0,+-d)　となります。交点とは、k(m-b*i) - k(s)　を実行することなので、(0,+-b)の虚部にマイナスを掛けておいてから (0,+-d) を引きます。(0,-+b) - (0,+-d) = (0,-+b+-d) となります。ですから、ここをpn(s)の実零線（緑線）が必ず通ることになります。そこで、ここに緑点を打ちます。

赤横線とは、a=0.5軸上の虚零線の零点を通るので、(+-a,0)の値をとります。赤線はk(s)の虚零線なので、(+-c,0) の値をとります。虚部は零なので、マイナスを掛けても変化がないので、このまま引き算します。 (+-a,0) - (+-c,0) = (+-a+-c,0)　となります。答えの虚部が零なので、ここをpn(s)の虚零線（桃線）が必ず通ります。そこで、ここに桃点を打ちます。

色違いの交点は零になるわけではないので、そのままにしておきます。






■１０の３５■　　　　　　区域計算



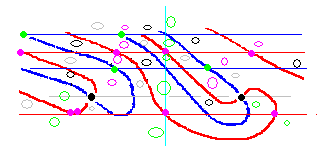交点が決まったら、区域計算をします。

a=0.5軸上の値は k(s)の形から判定します。それによって　(+,+)とか、(-,+)などの符号が定まります。これと並行の箇所にあるk(s)の区域の符号を調べます。すると、そこも　(-,-) などの符号が定まります。k(m-b*i) のｂにマイナス符号が付いているので、a=0.5 上の符号も虚部にマイナスを掛けて、符号を逆転させる必要があります。その上で、k(s)の符号を引きます。(+,-)-(-,-) などの計算になります。答えは　(+,?) となります。「？」の意味は、「プラスにも、マイナスにもなりうる」ということで、零線が通ることが出来ることを示しています。

(?,+), (?,-) という結果になった区域には細線で緑丸のしるしをつけておきます。そこは緑線の通ることのできる区域です。(+,?), (-,?) という結果になった区域には細線で桃丸のしるしをつけておきます。そこは桃線の通ることのできる場所です。(+,+), (+,-) などの結果になった区域は、細線で黒丸をつけておきます。緑線も桃線も通れない場所です。(?,?) となったところには細線で灰色丸をつけておきます。そこは緑線も、桃線も通ることのできる場所です。


この区域計算をすべての区域で行う必要がありますが、以下のやり方で簡略化することができます。

ｍ軸上の区域はすべて緑丸。

緑丸の区域と同種の交点の反対側は緑丸区域。異種の交点の反対側は桃丸区域

黒丸区域の同種の交点の反対側は黒丸。異種は灰色丸。

緑丸と接する青線の反対側は黒丸で、赤線と接する反対側は灰色丸。赤丸と青線で接する反対側は灰色丸で、赤線と接する反対側は黒丸です。

灰色線の上下は同じ色丸なので、無視します。







■１０の３６■　　　　　　緑線、桃線を引く



次に、零線を引くことになりますが、色付き交点は必ず通らなければならないので、交点から線を引き始めます。通れる方向へと線を伸ばします。

緑線は青線を超えることはできません。その理由は、青線のある場所は　k(m-b*i) か k(s) のいずれかが (0,+-b) となっている場所です。この場所でのpn(s)の値は、(0,-+b) - (+-c,+-d) を実行すること、もしくは、(+-a,-+b) - (0,+-d)　を実行することですから、答えは　(-+c,-+b-+d) もしくは　(+-a,-+b+-d)　となり、実部は必ず　-+c、+-a　という値をとり、零になりません。しかし、赤線は超えることが出来ます。なぜなら、(+-a,0) - (+-c,+-d) = (+-a-+c,-+d) 、(+-a,-+b) - (+-c,0) = (+-a-+c,-+b) となり、実部が零になる可能性を持っているからです。たとえば、a=c　のとき、a-c=0 となります。

同じ理由で、桃線は赤線を超えることはできません。(+-a,0) - (+-c,+-d) = (+-a-+c,-+d) となり、虚部が零にならないからです。しかし、青線は超えることが出来ます。(0,-+b) - (+-c,+-d) = (-+c, -+b-+d) ですから、b-d　のとき、もしくは　-b+d　のとき、零となることがあるからです。

緑線は、緑丸と灰色丸区域を通れます。桃線は桃丸と、灰色丸区域を通れます。その先に同じ色の交点があればそこを通過します。リーマン零点は、この図の中では交点ではないので無視されます。通過可能であっても、何も通過しない区域もあります。




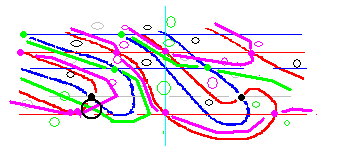その結果の一例が右の図です。

pn(s)は微分係数の一致がないので、緑線と桃線は直交する必要はなく、閉鎖空間を作っても矛盾とは認定されません。ですから、かなり自由な作図が可能で、いくつかの可能性が残るのが普通です。





微分係数が一致しないことは、証明する必要はありませんが、計算上、一致しないことを示しておきます。

たとえば、(-2,10)の点におけるpn(s)のa方向での微分係数は　(1.3570079E0, 1.1097167E0)、 b方向の微分係数は 　(-1.1061232E0, 1.7179153E0)　です。普通は、aの微分実部とbの微分虚部が一致するのですが、一致しない関数もあります。

この作図では、左側の緑線と桃線はそれぞれ横Ｕ字形を作っています。pn(s)としては、普通は零線が右に流れる形になるので、この場合もできれば右に流れるように作図したいという思いがあります。しかし、a=0.5を含む区域はすべて緑丸で、緑線だけが通れる場所です。桃線はa=0.5を通過する赤線の場所だけしか通れません。ところが、この点はすでに上側からくる別の桃線が通過していて、左からくる２本の桃線の通り道がありません。そこで、このふたつは必ず繋がって横Ｕ字形になります。すると、この２本の桃線の間を走っていた緑線は桃線の横Ｕ字形を超えることになり、その際、a<0.5 の範囲に必ず交点が発生します。その交点を太線の黒丸で示しておきます。交点とは pn(s)の零点のことです。



pn(s)の零点が必ず発生することがリーマン証明完成への関門のひとつとなります。ここまでがはたして正しいかどうかは、証明公表後にさらに検討しますが、ここはひとまず先に進みます。

＜付論＞　　　緑線が横Ｕ字形になるかどうかは、証明には直接関係ないので、議論しませんが、右に流れる作図が出来るかどうかを検討すると、結構複雑な議論が必要になります。







■１０の３７■　　　　　　pn(s)の零点とは何か


pn(s)の零点は左側だけでなく、右側（a>0.5）にも発生していますが、片方だけで証明は完成するので、今後は左側（a<0.5）の零点に注目して証明を進めます。

零点とは緑線と桃線の交点です。これは　k(m-b*i)-k(s) が零の点なので、k(s)に翻訳しなおして考えると、交点上のk(s)の実部、虚部の値と、そこを通る横線とa=0.5軸が交わるところのk(s)の値が一致しているということです。

このような点がk(s)内にあるなら、それはpp(s)にも反映します。つまり、この交点上で、k(m-b*i)/k(s) を実行すると、分子・分母が同じなのですから、答えは　(1,0) となります。

つまり、pn(s)に零点があるなら、pp(s)には 同じ場所に必ず(1,0)点があることになります。

ここまでの論理が、証明完成への第二関門となります。ここまでは正しいでしょうか。これについては、あとで検討することにして、先に進みます。







■１０の３８■　　　　　　pp(s)の (1,0) 点が存在しないことの証明



(1,0)点の不存在こそがver51証明の中心だったのですが、仮定上の零点があるという前提では　(1,0) 点は必ず存在することが判りました。これでは証明は成り立ちません。

どうしてそのように言えるかというと、仮定上のpp(s)の図では、リーマン零点がa=0.5上にはなく、零線図左右にそれぞれひとつづつあります。証明としては左側のみに注目するので、この区域にはひとつだけ存在します。ですから、そこを通るk(s)の実零線と虚零線があり、その零線図を使ってpp(s)の零線図を描くことができます。pp(s)の場合、この点は零で割るので、特異点となります。ここをpp(s)の虚零線が通過します。その前にpp(s)の実零線と交差しているので、虚零線上の実部値は零を通過したのち、無限に至ります。すると、その途中で必ず１を通ることになります。つまり、このあたりの虚零線のどこかに(1,0)点が存在することになります。ここがpn(s)の(0,0)点ということであり、何も問題ないということになります。矛盾を指摘することはできません。



pp(s) = k(m-b*i)/k(s) 　ですが、m=0.5 のときの零線図はすでに示してあります。このとき、その左半分（a<0.5）に　(1,0)点があるかどうかということです。また、(1,0)点がないことをどうやって証明するかです。

実際にあるかどうかを、計算できる範囲で調べてみました。

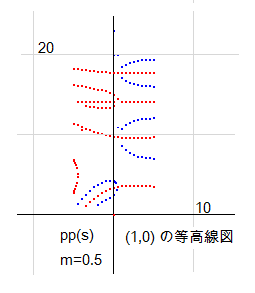
実部１、虚部０　の等高線図を計算で求めると右図のようになります。

等高線（青線）と虚零線（赤線）の交点が (1,0)点を意味します。この図の中ですでに (1,0)点が発生していますが、それはすべてa=0.5上にあるように見えます。証明としては、この交点が　a<0.5　に存在しないことを示せばよいのですが、この図の範囲ではなさそうに見えます。

では、これを計算ではなく、論理として証明してみます。


ここでも背理法を使います。まず、pp(s)の a<0.5 に(1,0) 点が存在すると仮定します。すると、「その点を通過する実部１等高線と虚零線がある」、もしくは、「そこが実部の頂点となっていて、そこを通る実部１の等高線がなくて、虚零線のみが通っている」　かのいずれかに場合分けすることができます。

まず、等高線がある場合を検討します。等高線があるということは、それが途中で途切れることはありませんから、どこかに繋がっていなければなりません。まずは、左側の無限に繋がること、上側の無限につながること、右にはすでに実零線がありますが、それに繋がること、下のb=0線に繋がること、さらに、自ら輪になることの５通りが考えられます。






■１０の３９■　　　　　　左・上の無限に繋がらない証明、b=0 の線に繋がらない証明


a→ -∞　の k(s) の値は、サイン波になっているので、ときどき零が現れます。これだと判りにくいので、絶対値で考えます。k(s)の絶対値は、a→ -∞　で、常に増加し、最後には無限大になります。

k(0.5-b*i) の絶対値は、任意のｂの値に対して有限ですから、a→ -∞　で　pp(s) = k(m-b*i) / k(s) は零に近づきます。

pp(s)は分子にk(0.5-b*i)を持っているので、リーマン零点のところで常に(0,0)になります。これは零線図で左右の無限大に繋がる青赤の横線として現れます。リーマン零点はｂ方向の上にもあるので、上側にも横線は無限に存在し、現れなくなることはありません。

さて、青赤横線は零線です。その零線の近傍には極小の等高線が走っています。その先には少し大きな等高線が走っています。それらの等高線の値は零ではないので、左の無限大に繋がることはなく横Ｕ字形として存在しています。

もし、実部１の等高線が左半分に存在するなら、その線は左の無限大に向けて進むことはできません。なぜなら、左側には必ず 0.9の等高線が存在して、１の等高線はそれを超えることが出来ないからです。同じように、上の無限大に向けて進むことはできません。なぜなら、上側にも0.9の等高線があるだけでなく、零の等高線、つまりpp(s)の実零線が横に走っているからです。下側にも実零線があり、１の等高線はそれを超えることはできません。ゆえに、左、上、下には繋がらないことが証明されました。






■１０の４０■　　　　　　右の実部１横Ｕ字形に繋がらない証明


a>0.5 には実部１横Ｕ字形があります。kv(s)の第１、第２、第４虚零線・・・と a=0.5 で交差していて、交点の値は　 (0.5, 3.43621)、　(0.5, 9.666908)、　(0.5, 17.8455)　となっています。kv(s)の虚零線との交差は繰り返し現れます。計算上、実部等高線が a=0.5を超えることはありません。しかし、証明ですから、何らかの論理が必要となります。

そこで、また仮定法ですが、もし、実部１等高線がa=0.5を超えて左側に進出したとします。すると、a=0.5上に等高線との交点が２か所生じることになります。一方、pp(s)はkv(s)とa=0.5において同じ値をとります。もし、pp(s)に２か所実部１の点があるなら、kv(s)にも実部１の点が２か所あることになります。ところが、kv(s)の絶対値は常に１なので、実部１なら虚部の値は零でなければなりません。また、角度も確定して必ず零になります。しかし、kv(s)の角度は公式が見つかるほどきれいに増加（左周り回転）する関数ですから、同じ角度なら２＊π離れていなければなりません。近傍に角度零の点がふたつ並ぶことはありません。そして、２＊π離れたところには、すでに別の虚零線が通っているのですから、その間に別の虚零線が通ることは不可能です。ゆえに、このような矛盾が発生するので、実部１等高線がa=0.5を超えることがないことが証明されました。






■１０の４１■　　　　　　輪になることがないことの証明


さて、上下左右に繋がらないので、もうひとつの可能性を検討します。それは実部１等高線が自らに繋がって輪を作ることです。

pp(s)は、微分係数が一致しないので、輪になること自体は矛盾ではありません。しかし、輪になるなら、その輪を虚零線が通過することになります。虚零線は等高線と、接触する形でなければ、必ず一時的に輪の中に入ります。すると、外に出るとき、もうひとつの、(1,0)点を通過することになります。つまり、(1,0) 点はふたつなければなりません。しかし、もし、ふたつあるなら、pn(s)の交点もふたつあることになります。pn(s)の緑線が桃線と交わり、再度、交わると、緑線は桃線の外に出てしまい、左上からの緑線につながるためにはさらにもう一度桃線と交差しなければならなくなります。すると、今度はpp(s)点の３つ目が必要になり、そのためには４つ目のpn点が必要になり、次に５つ目、６つ目と無限に必要な交点が増えてゆきます。無限に増えることはできないので、これは矛盾となります。

もう一つの可能性は、等高線と虚零線が接する形で輪の中に入らないことです。微分係数の一致がないので、接することも検討対象です。

そこで、pp(s)の(1,0)を通る虚零線がわずかに伸びた点を s2(x2,y2) とします。pp(s2) = p2+q2*i　とします。a=0.5上の並行点は (0.5, y2) となります。すると、s2は等高線の外にあるので、p2は必ず１以下の数になります。q2は虚零線の上なので零です。これを別表記にすると、k(0.5-y2*i) / k(x2+y2*i) = p2 となります。虚部は零で等しく、実部分母は分子より大きいという条件で、これをpn(s)に移行させます。すると、k(0.5-y2*i) - k(x2+y2*i) の実部は、必ずマイナス、虚部は零になります。

次に、(x2,y2) に対して逆方向に伸びる虚零線を考えます。(1,0)点の近傍の点 s3(x3,y3) とします。pp(s3)=p3+p3*i　となります。その時の s3は等高線の外ですから、p3は必ず１より小さくなります。q3は虚零線の上ですから零です。するとpp(s)を示すk(s)の式は、k(0.5-y3*i) / k(x3+y3*i) となり、その答えが　(p3,0) ということです。そして、p3が１以下ということです。そこで、これをpn(s)に移行させます。pn(s) = k(0.5-y3*i) - k(x3+y3*i) の実部は、必ずマイナスになります。虚部は零です。

pp(s)の (1,0)点はpn(s)の零点です。ここで緑線と桃線が交わっていて、緑線により実部はプラスとマイナスに分けられています。ところが、零点の両側のs2とs3がともに実部マイナスとは、ここを緑線が通っているならあり得ないことです。これは矛盾と認定できます。ゆえに、このような矛盾を生じさせる仮定は成り立たないのであって、虚零線は等高線に接触する形にはならないことが証明されました。






■１０の４２■　　　　　　頂点にならないことの証明　　　
「１０の４２」の証明は間違っていたので撤回します。


あとひとつ、頂点のときがまだ残されています。

(1,0)点が実部頂点のとき、そこを等高線が通ることはありません。虚零線のみが通ります。この場合も、先の接線の場合と同様に、虚零線上の近傍点 s2(x2,y2) を考えます。反対側の点を s3(x3,y3)　とします。pp(x2+y2*i)=p2+q2*i　とし、pp(x3+y3*i)=p3+q3*i　とします。虚零線上の点なので、q2, q3　は零となります。p2, p3 は頂点ではないので、必ず１以下になります。pp(s) = k(0.5-b*i) / k(s)　なので、k(0.5-y2*i) / k(x2+y2*i) = p2、　　k(0.5-y3*i) / (k(x3+y3*i) = p3 となり、分母は分子よりも大きくなります。

この条件で、pn(s)に移行します。k(0.5-y2*i) - k(x2+y2*i) は p2 が１より小さいので、必ず実部マイナスになります。k(0.5-y3*i) - k(x3+y3*i) も同じで、p3　が１より小さいので、必ず実部マイナスになります。すると、pn(s)の零点において、実零線（緑線）が通っているにも関わらず、零点の両側、s2とs3が同じ符号になっています。これは矛盾です。ゆえに、最初の仮定である(1,0)が頂点になることはないことが証明されました。

これで、すべての場合に矛盾が生じたことになります。ゆえに、(1,0)点は存在しないことが証明されました。






■１０の４３■　　　　　　証明完成


pp(s)の　a<0.5　に(1,0)点が存在しないということは、pn(s)での零点が存在しないことを意味しています。零点が存在しないとは、pn(s)の緑線・桃線が交わらないことを意味しています。交わらなければ、a=0.5を超えて右に流れるしかありません。しかし、零線が右に流れることのできない零線図になっています。これは矛盾です。

このような矛盾が生じるということは、一番最初に仮定したこと、つまり、k(s)の仮定上の零線図が成り立たないということであり、リーマン零点が横に並んで存在するという最初の仮定が間違っていることを証明しています。














以下、ver20

証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部

以下、ver35

証明の第９部、第１０部










表紙に戻る



ご感想、ご質問、その他のご意見は、Mailのアドレス（bp5h-krs@asahi-net.or.jp）へお願いします。