リーマン仮説（リーマン予想）の証明

pw(s)　による証明





ver57 は失敗でした。証明の最後に登場するk(s)右無限値は、回転角度零では　(1,0)　ですが、角度が増加すると　(1,0)　から離れます。ver57 は 常に (1,0) であると考えて証明を進めたものなので、撤回せざるを得ません。また、いずれ、気を取り直して、新しい証明にチャレンジしたいと思います。

２０１７・４・３０










pw(s)による証明は、過去の証明を再検討する中から生まれたアイデアです。うまくいっているように思えても、結局失敗に終わるというのが今までの流れです。もう以前のような自信はなくなりました。しかし、今のところ正しいと思える証明を放置するわけにはいきません。今後、より細部まで厳密に検討して、もし、間違いがあるならそれを修正して、完成を目指したいと思います。

最後に間違っていることが判明することが多いので、今回も最終段階のところだけを公表します。これが間違っているなら、あとのところを証明しても無意味だからです。この公表部分が正しいなら、後日残りの部分も証明して完成となります。






■　　　　　　pw(s)　の定義


まずは、定義から説明します。


pw(s) = k(s) - k(m-b*i)



ver55で取り上げたpn(s)と似ていますが、その修正版です。k(s)が先に来ていることと、0.5が m という任意の定数に変わっています。

m は任意ですが、この証明ではもっぱら左リーマン零点の場所を意味します。左リーマン零点は仮定上の点なので、数字を特定することはできません。しかし、0 から　0.5　までの数であることはわかっています。当面、例示する必要があるときは　m=0.3　とすることにします。

さっそく、m=0.3として、pw(s)の零線図を描いてみます。


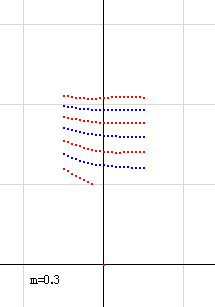
a=0.3のところに青の縦線が走っていますが、この図では省略されています。青縦線があると思ってください。




pn(s)とほとんど同じ図が出来上がりましたが、微妙な違いもありますから、もちろん別物です。













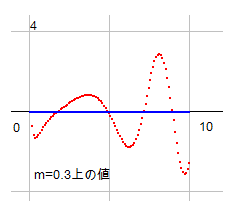
基準となるのは m です。m=0.3　として、基準軸上の値を確認しておきます。

ｍ上の実部が零となるのはpn(s)と同じです。虚部の値は、pn(s)と異なり、公式化されていません。












■　　　　　　pw(s)は不一致関数




pw(s)は不一致関数です。不一致関数とは、a方向の実部微分係数とb方向の虚部微分係数が一致しない関数ということです。併せて、a方向の虚部微分係数とb方向の実部微分係数がマイナスを介して一致しません。普通の複素関数はこれらが一致することはver55で説明したとおりです。

参考までに、一致関数であるk(s)がどうなっているかを示しておきます。

k(s)の(1,10)点での微分係数は　a方向で　(-2.6227404E-1, 2.2271088E-2)　となっています。b方向では　(-2.2271157E-2,　-2.6227415E-1)　となっています。aの実部とbの虚部が一致していることが確認できます。他の点でも結果は同じです。この現象は普通の複素関数で成り立っています。

ところが、この法則が成り立たない関数があります。それが不一致関数です。pw(s)の(1,10)点での微分係数は、a方向で　(2.6227404E-1, 2.2271088E-2) , b方向で　(-4.3248055E-2, -6.7114637E-1)　となっています。a実部微分とb虚部微分が一致していないことが確認できます。

ちなみに、微分係数引き算の法則は成り立っています。pw(s)の定義は　k(s)-k(m-b*i)　ですから、k(s)の微分係数からk(m-b*i)の微分係数を引くとpw(s)の微分係数になります。

m=0.3としておきます。(1,10)点におけるk(s)の微分係数は　a方向で　(-2.6227404E-1, 2.2271088E-2) で、b方向は　(-2.2271157E-2, -2.6227415E-1)　です。　k(0.3-b*i)　は　a方向で　(0, 0)　、b方向で　(2.0976898E-2, 4.0887222E-1)　となっています。

引き算すると　a方向は　(-2.6227404E-1, 2.2271088E-2) , b方向は　(-4.3248055E-2, -6.7114637E-1)　となり、pw(s)の微分係数とぴったり一致します。



pw(s)は不一致関数なので、実零線・虚零線の直交は保証されなくなりますし、輪（閉鎖空間）になることも矛盾とは言えません。仮定上の零点がある場合の作図は、自由度が増すので、いろいろな可能性を検討しなければならなくなります。しかし、まったく無制限ということではありません。左上から降りてくる零線の数は同じであり、右に流れる零線の数と一致しなければなりません。k(s)とk(m-b*i)の作る交点を通らなければなりませんし、通れる区域も決まっています。ですから、矛盾が生じるかどうかを検討することができる程度には確定します。






■　　　　　　複素回転とは


複素回転については　ver35で解説してあるのでそちらも参照してください。複素数は極座標表示が可能です。s=a+b*i　とすると　a=r*cosθ、　b=r*sinθ 　と表示することができます。このθを変化させると a, b は変わり、実部波・虚部波は変化します。しかし、2*pi　で元に戻ります。零線図は零点の集まりなので、プラスマイナスは関係ありません。ですから、piで元に戻ります。

零線図は波を打つように変化します。図そのものが回転するわけではありませんが、2*pi で元に戻る構造は回転と同じです。ゆえに、複素角変化を回転と呼ぶことにします。極座標表示の図（ｒθ図）にすると実際に回転します。

pw(s) m=0.3　の零線図は、回転させると次のように変化します。



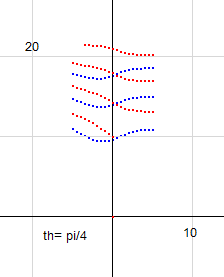
角度零の図はすでに載せています。右図は角度 pi/4 の図です。青線が赤線に近づき、赤線が青線に近づいています。pi/2で相手側の場所まで移動するので、pi/4とは、丁度半分ということです。

















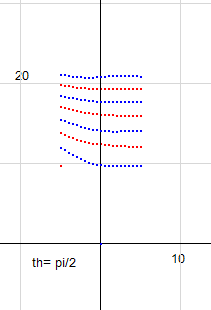
回転角度 pi/2 で相手側の場所まで移動します。右図はその確認のためのものです。先の角度零の図と比較すると、青線と赤線が入れ替わっていることがわかります。





















■　　　　　　零線の組み換え




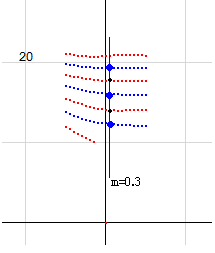
pw(s)は角度零のとき組み換えを起こします。k(s)のような横Ｕ字形はないし、微分係数も一致しないので、組み換えのシステムは少し異なりますが、組み換えを起こす場所が微分零になっていることは同じです。ｍ軸上の青交点が組み換え点です。

不一致関数の場合、t1*cosθ、t1*sinθ　という微分係数の公式が成り立ちません。実部と虚部は別々に動きます。ですから、式にすると　t1_re*cosθ、t1_im*sinθ　という具合になります。これについては、今回の証明（ver57）に直接関係ないので別途詳しく説明する予定です。また、一部、検討中のところもあり、確定した結論ではありません。先の式も　t1_im*cosθ　と書くべきかもしれません。各角度ごとに異なるt1が存在するので、t1_th　と表現すべきかもしれません。・・・それはそれとして、pw(s)の角度零の図では実零線の青交点が存在し、そこが　t1_re=0 となっているということです。








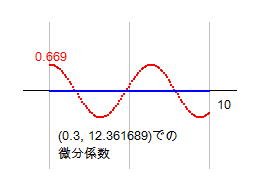
参考、および、確認のため、このt1_re=0点を中心とするひとまわりの微分係数の図を載せておきます。m=0.3　のとき、b=10より上の青交点の場所は　(0.3, 12.361680)　です。この点のまわりの微分係数は、実部微分すべて零です。ゆえに、この点は t1_re=0点、もしくは、th=0でのt1=0点と認定できます。









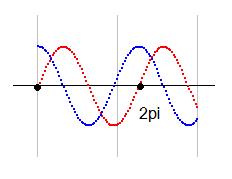
角度を増加させると零線図が変化します。その変化の仕方はサインコサイン図から判定します。

一番下の青交点の左青線上側は (-,-) です。この青線が角度増加するとどうなるかは、サインコサイン図の(-,-)領域で調べます。青赤ともにマイナスなのは図の中央部分ですが、この中の青線は2piの手前にあります。この点の実部の値は零です。この点の角度が増加すると、値はプラスに変わります。ですから、実零線図でも青線上はすべてプラスに変わるので、マイナス部分がへこむことになります。この図で説明すると、青線が上に移動するということです。

青交点の右側の青線の上側は　(+,-)区域です。そこでサインコサイン図の(+,-)領域に注目します。そこは2piより左の区域ですが、その中にある実部零点は先に分析した点と同じところなので、角度増加によりプラスに変化します。ですから、零線図でも青線上はプラスに変化するので、下にずれることになります。

虚零線についても同じ作業をします。今の青交点の上側に実虚零点があります。その左側の上側は (-,+) なので、サインコサイン図の中央より左の領域に注目します。この領域の虚部零点はpiの値のところです。ここで角度増加が起きると、値はマイナスになります。ですから、零線図でも赤線上はマイナスになるように変化します。つまり、上にずれます。同じように左側の虚零線上側は (+,+) なので、この領域の虚部零点は角度０のところにあります。この点で角度増加が起きると、値はプラスになります。ですから、零線図上の赤線は下にずれることになります。

その他の実零線、虚零線も同じ方向にずれます。零線図の一部だけ分析すれば、全体の動きを判定することができます。


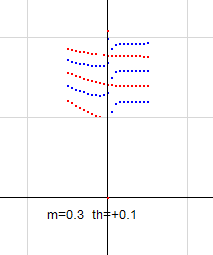
実際の零線図で確認してみます。回転角度を　th=0.1　として計算すると右図のようになります。左側の青線は上にずれ、右側の青線は下にずれています。赤線のずれは小さいのではっきりしませんが、詳しく見ると、左の赤線は上に、右の赤線は下にずれているので、上記の分析が正しいことが確認できます。。
















■　　　　　　t1=0点がある場合


t1=0点とは、t1*cosθ　のt1が零ということです。このような点は角度θに関係なく微分係数が零になるので、零線組み換えが起こりうる場所になります。

零線図を複素回転させると、池に波が立つように、実零線が伝わってゆきます。普通は形を変えながらも一本の線が移動するだけですが、k(s)の場合、ときどき実部・虚部ともに横Ｕ字形のところがあり、そこを一本の波のまま通過することはできません。そこで、波同士が合体するように、２本の線が合体し、それぞれの組手の相手を変えてまた移動を始めます。

pw(s)では、実部・虚部ともに横Ｕ字形になるところがないので、実際の零線図を載せることはできませんが、その他の不一致関数でも横Ｕ字形が並ぶことは、今のところ見つかりません。やむを得ず、k(s)を使って説明しますが、k(s)のt1=0点は (2.4631568, 23.298319) にあります。ここで零線組み換えが起こります。



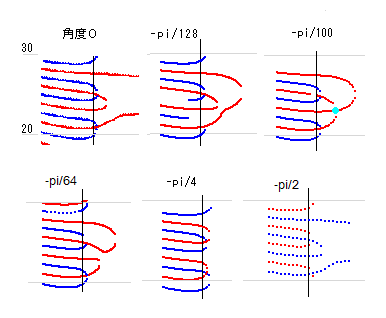
-pi/128 回転させると上と下の虚零線が繋がります。-pi/100 あたりで内側の虚零線と外側の虚零線が繋がります。その後、-pi/64で上と下の虚零線が分れ、-pi/4　で完全に分離します。-pi/2 で実零線は虚零線のところへ、虚零線は実零線の場所に移動していることが確認できます。、


pw(s)でも同じような組み換えが起きていることはすでに示しています。

仮定上の零点がある場合、零線がかなり無理と思える動きをしたうえで組み換えが起こります。常識的にはありえない動きですが、それを矛盾と判定することができない場合がほとんどなので、k(s)の複素回転を根拠とする証明はことごとく失敗に終わっています。pw(s)も仮定上の零点がある場合、複素回転はk(s)同様の複雑な動きになりますが、k(s)と違いひとつ条件が増えているので、矛盾と判定することができます。

まずは、仮定上の零点があるk(s)の零線図で、組み換えを含む回転がいかに複雑であるか、そして、それにも関わらず矛盾という判定はできないことを示しておきます。その上で、pw(s)では、k(s)と同様の動きなのに、なぜ矛盾と判定できるかを説明することにします。





■　　　　　　仮定上の零点がある場合の複素回転と組み換えを起こす仕組み


組み換えを起こして回転できるかどうかがこの証明（ve57)の矛盾判定基準となるので、詳しく説明しておきます。

仮定上の零点がある場合、実部、虚部ともに横Ｕ字形になることがあります。図がやや複雑なので、そのままでは回転させることができません。それで零線組み換えが必要になります。



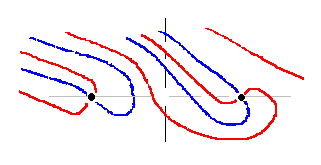
具体例として事例（１、３、６）を取り上げます。事例分類の仕方はver35で説明しているので、そちらを参照してください。リーマン零点が左実部横Ｕ字形の下側と、右実部横Ｕ字形の上側にあり、虚零線については、第１、第２が繋がり、第３、第４が繋がっている形です。









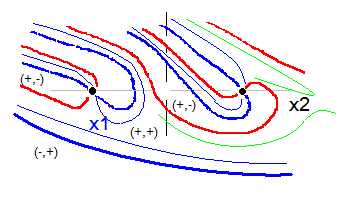
角度を増加させると、(-,-)部分にある青線はマイナス方向に移動し、(+,+)区域にある青線はプラス方向に移動します。結果は細青線のようになります。

さらに増加させると、x1でふたつの青線が繋がり、左側の線は赤線方向へ右側の線は緑線の方向へと進みます。その後の青線は緑色で示します。緑線は上に移動してx2で右青横Ｕ字形から移動してきた緑線と合流し、組み換えを起こします。左側の緑線はそのまま赤線の場所に移動し、右側の緑線はさらに上って一番上の赤線の場所に到達します。

合計２個の組み換え点で回転は完了します。

虚零線は、それほど複雑ではありません。(-,-)区域にある赤線は上に移動し、リーマン零点より上の赤線も上に移動し、そのまま青線の場所に到達します。組み換え点は必要ありません。右の赤横Ｕ字形も同じです。

零線がありえないほど激しく動き、めったに発生しない組み換え点（t1=0点）がふたつも発生しますが、矛盾であるとは証明できないので、この動きを認めるしかありません。よって、（１、３、６）は回転において矛盾を発生させません。





■　　　　　　pw(s)での仮定上の零点がある場合


pw(s)の場合はどうでしょうか。事例（１、３、６）を使って説明します。

仮定上の零点がある零線図を描くにはk(s)の零線図とk(m-b*i)の零線図が必要になります。k(s)の零線図は先に載せてあります。k(s)の零線図にk(m-b*i)の零線図を重ね、同じ点どうしの引き算を実行するとpw(s)の零線図になります。




k(m-b*i)の零線図は、k(s)のa=m上の値だけで決まります。a=m軸が零であれば、その横線が零線となります。ですから、実部零点には青横線を引きます。虚部零点には赤横線を引きます。リーマン零点は実部零、虚部零なので、青赤横線を引きます。（零線図の作り方については、後日、さらに詳しい解説を載せる予定です。）

青横線と青線の交点はpw(s)の実零線が通るので緑点を打ちます。赤横線と赤線の交点はpw(s)の虚零線が通るので桃点を打ちます。青赤横線と青線の交点には緑点、赤線との交点には桃点を打ちます。

リーマン零点を含むｍ軸上にはpw(s)の実零線が縦に通っています。ですから、ここには緑線を引いておきます。この線上のどこでも緑線は通過可能です。ゆえに、青線との交点には緑点を打ちません。しかし、赤横線との交点には桃点を打ちます。リーマン零点上もpw(s)の虚零線は通るので桃点を打つべきですが、リーマン零点の場所がわからなくなると困るので、ここにはうちません。しかし、虚零線（桃線）は通るとご理解ください。






■　　　　　　区域判定のやり方


次に、零線で区切られた区域をどの零線が通れるかを判定します。pw(s)の実零線を緑線とします。虚零線を桃線とします。緑線の通れる区域と桃線の通れる区域、どちらも通れる区域、どちらも通れない区域の４通りがあります。

その判定方法は区域計算によっておこないます。k(s)の区域の符号を調べます。実部がプラス、虚部がプラスなら、その区域は　(+,+)　と表示されます。実部がマイナス、虚部がプラスなら　(-,+)　です。k(m-b*i)も同じように調べます。k(m-b*i)はk(s)と虚部の値が逆になります。k(s)のｍ軸上の値が (+,+) なら、k(m-b*i)　は　(+,-) となります。

区域計算の具体例として、k(s)を　(-,+)、k(m-b*i) を　(-,-) とするなら、(-,+) - (-,-) を計算することになります。実部がマイナスで、そこからマイナスを引くとプラスになることもあり、マイナスになることもあります。このようにどちらにもなりうる時の答えは　？　という記号にします。虚部はプラスからマイナスを引く計算ですが、この答えは必ずプラスになります。ゆえに、答えは　(?,+)　となります。実部が　？　とは、実部が零になることもあるという意味なので、ここを緑線が通れると判定します。虚部はプラスなので、零になることはありません。ですから、桃線は通れないと判定します。

このような計算を全区域でおこないます。ただし、計算は面倒なので、実際は簡略化した判定方法を使います。ｍ軸上の区域はすべて緑線しか通れません。ですから、ここに緑丸を付けておきます。緑丸区域と青線で接する区域はどちらの零線も通れないので、黒丸を付けます。また、緑丸と赤線で接する区域はどちらの線も通れるので、灰色丸を付けます。

黒丸と赤線で接する区域は桃線しか通れないので、桃丸を付けます。桃丸区域と青線で接する区域は、どちらの零線も通れるので灰色丸区域です。



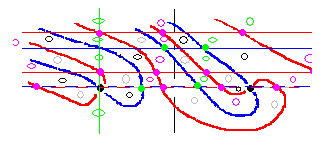
青赤横線と接する区域は別の判定方法を使います。緑丸区域の反対側は桃丸区域、黒丸区域の反対側は灰色丸区域となります。

これですべての区域の判定が可能になります。

右図はその結果を図示したものです。






■　　　　　　緑線、桃線の引き方


以上の分析を基にして緑線、桃線を引きます。

pw(s)は不一致関数なので、零線を引く自由度は大きいのですが、結果的にはひとつの図に収斂します。というのは、緑線と桃線は交差することは可能ですが、交差すると、そこがpw(s)の実虚零点となり、あとで述べるように零線組み換えの必要が生まれ、矛盾の発生する場所になります。証明の作業としては、最初から矛盾が生じるようでは困るので、なるべく緑線と桃線は交わらないように作図する必要があります。

また、緑線も桃線もｍ軸より左側では必ず青線、赤線に沿って下ってくるので、そこから外れると繋がる相手がいなくなります。また、ｍ軸より右側では、青線、赤線と離れて横に流れます。そうしないと右無限で矛盾が生まれます。ですから、作図した結果は、線のふくらみが大きいかどうか程度のことで終わります。






■　　　　　　零線図を回転させる



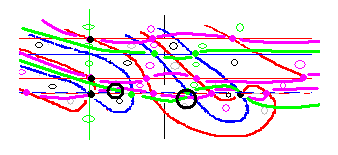
事例（１、３、６）の場合は右図のような零線図（緑線、桃線）になります。緑線は左リーマン零点は通りませんが、ｍ軸上を緑線が通っているので、ここもpw(s)の実虚零点となります。桃線は右左のリーマン零点を通ります。その結果、pw(s)の実虚零点は、この図の中では合計６つ生じることになります。交点は太線の黒丸のところです。

これが複素角零の零線図です。これを複素角pi/2 回転させると、実零線は虚零線の場所に移動し、虚零線は実零線の場所に移動します。また、そうならなければなりません。そのために零線の組み換えが必要ならば組み換え点（t1=0点）で組み換えを行います。ただし、実虚零点は動きませんし、動かしてはなりません。そのような点が６つもあるのですから、回転を実現させることは容易ではありません。はたして回転可能かどうかということです。

そこで、すこしずつ角度を増加させて、零線がどう動くかを確認してみます。角度を増加させると、零線は移動します。どちらに動くかは、先に載せてあるサインコサイン図で判定します。

(-,-)区域に接する青線はマイナス領域に張り出します。この区域の赤線はプラス領域に張り出します。区域の符号は、仮定上の話なのでプログラム計算できません。黒丸区域の区域計算の結果をメモしておくと便利です。ひとつ前の図で、左リーマン零点の左側が黒丸区域であることがわかります。この場所のk(s)は　(+,-)、k(m-b*i)は　(-,+) なので、(+,-) - (-,+) = (+,-)　という区域計算になります。pw(s)の実部はプラスなので、この区域を含む緑線で囲まれた枠全体がプラスと判定できます。虚部はマイナスなので、この区域を含む桃線で囲まれた枠全体がマイナスと判定されます。すると、この区域の隣の緑領域の符号は (-,-) となるので、そこの緑線は上に移動すると判定できます。下にある桃線も上に移動すると判定できます。



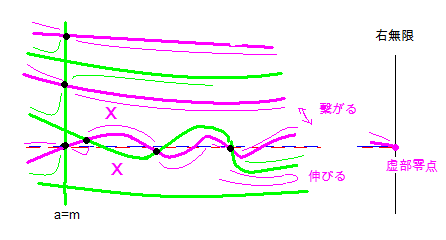
ひとつ決まるとあとは連動しているので、同じ方向に移動すると判定できます。その結果は右図の細緑線、細桃線で示してあります。

次に、この細緑線、細桃線がさらに同じ方向に移動すると考えます。そして、緑線は桃線に、桃線は緑線の場所に到達すれば回転は完成となります。そう思って作業すると、緑線はなんら問題なく桃線の場所に到達することがわかります。余る場所も、足りない場所もありません。

問題は桃線です。中央の桃線の移動方向には桃線があり、緑線に到達できません。別の桃線は実虚零点が邪魔になって、緑線に到達できません。そこで零線組み換えをします。組み換え点は桃Ｘ印のところです。仮定上の零点のない領域の桃線は、問題なく緑線に到達しています。ところが、仮定上の零点のある領域では組み換え点がふたつ必要になります。ここまでは矛盾とは言えません。

上側の組み換え点に桃線が集まったあと、左側の桃線はその先にある緑線に到達します。右側の桃線は右無限から上ってくる桃線と同じ線なので、短くなって緑線と同じ場所に到達します。下側の組み換え点に集まった桃線は、上側の桃線が実虚零点の間にある緑線に到達し、下側の桃線は、右無限に向けて張り出して、下側の緑線を含む残りの緑線の場所に到達します。これで回転は完了して矛盾は生じていません。

pw(s)以外の零線図では、上記の分析がそのまま通用して矛盾は生じませんが、pw(s)にはもうひとつの条件が加わっているので、話は別になります。





■　　　　　　もうひとつの条件を入れると矛盾が生じて回転ができない。


そこで、pw(s)の持つ、もうひとつの条件を説明します。pw(s)のｍは左側リーマン零点の場所です。ここを桃線が通りますが、リーマン零点は角度変化（回転）によって移動しない点なので、桃線も常にこの場所を通過します。そして、右無限において、k(s)は(1,0)となるので、pw(s) = k(s) - k(m-b*i) という計算式から、pw(s)の右無限の虚部零点はk(m-b*i)と同じ高さであることがわかります。つまり、左リーマン零点と平衡の右無限点は、常に虚部零点となり、桃線の到達点となるということです。これは角度変化（回転）によって移動しませんし、消滅もしません。

とすると、右無限にあった桃線が繋がって左方向に縮小することができなくなります。最後まで右無限に桃点が残り続けると、桃線が緑線に到達することができず、もしくは、到達しない部分が残ってしまいます。これは矛盾です。



このような矛盾の生じる事例（１、３、６）は存在しないことになります。


上の分析が正しいなら、証明の前提となる矛盾の構造が出来上がります。他の事例も（１、３、６）と似たようなやり方で証明できる可能性が大です。もっとも、今までの流れからすると、この段階で間違っていることが多いので、ここでこのやり方を公表しつつも、再度、厳密に検討し、本当に正しいと確信してから全体証明に移りたいと思います。













証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部

以下、ver35

証明の第９部、第１０部

証明の第１１部









表紙に戻る



ご感想、ご質問、その他のご意見は、Mailのアドレス（hirokuro303@gmail.com）へお願いします。