無矛盾性の証明も視野に入れて

ver64　　　　new 2017/10/27



ver60が失敗したあと、いくつかのアイデアを試したのですが、すべてうまくいきませんでした。それぞれ面白いアイデアで公表の価値はあると思うのですが、公表する前に失敗であることが判明したので、公表は差し控えます。しかし、バージョン番号は付けて保存しておくことにします。

自分なりに思いついたアイデアはすべて試しましたが、残るアイデアを試す気力はもうなくなりました。私の思いつく程度のアイデアでは証明はできそうもありませんし、おそらく証明はできないのではないかという気持ちもします。ですから、今後は「無矛盾性の証明」も視野にいれて、検討を続けたいと思います。

これからリーマン証明にトライする人のために、どこに問題があるかとか、どういう面白い現象があるかを記録しておこうと思います。




■　　　　　　k(s)　はゼータ関数の式


k(s)　を発見したことが、私のリーマン証明をトライすることの出発点です。この式は ver20 の第一部ですでに紹介しているものですが、まとめということで再度説明することにします。


k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }　

zt(s,n) = 1 + 1/2^s + 1/3^s + . . . + 1/n^s

ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

具体的にどのように計算するかは ver20 を参照してください。

ゼータ関数の定義と解析接続との関係には問題があるので、私としてはk(s)をゼータ関数として証明に取り組んでいます。k(s)がゼータ関数でないと考える人がいるかもしれませんが、それなら、k(s)をリーマン零点を計算する式としておきましょう。これに反論できる人はいません。

k(s)で、どのようにしてリーマン零点を計算するかも　ver20 や、「私の発見した数学公式」で説明してあります。



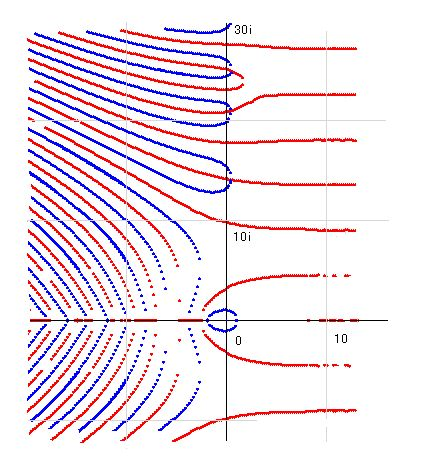
この式を使うと零点を計算できるだけでなく、零線図をきれいに描くことができます。


















■　　　　　　kv(s)　の発見


最初のうちはすべてが順調に進み、証明もうまくいくように思えました。kv(s)=k(1-s)/k(s) で定義される kv(s) が、　kv(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s }　と計算できることを発見しました。これにより、仮定上の零点があるなら、単独で存在することはできず、必ずペアになって、 a=0.5軸 から左右等距離のところに並ばなければならないことが証明できました。（ver20 を参照のこと。）



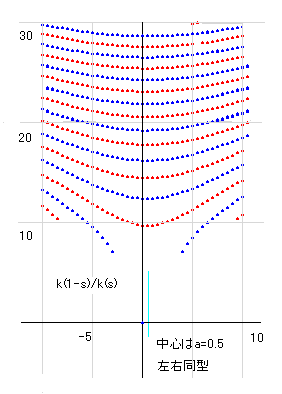
kv(s)の零線図は右のようになっています。





















■　　　　　　k(0.5+b*i)の角度公式を発見


kv(s)はk(s)と異なり、不規則振動が少なく、公式化できるところがたくさんあります。特に目立つのは、角度変化が　a=0.5 において、k(s)と連動していることです。右肩上がりと、右肩下がりの違いはありますが、ちょうど２倍の関係になっています。最初の　b=0　のところから誤差なしで一致しているので、完全イクオールの関係にあります。近似式を求めたところ、ある程度収束してくれたので、完全公式発見にトライしたところ、見事見つけることができました。これは私の自慢の公式の一つです。この公式については「私の発見した数学公式」ＨＰとver35で解説してあります。

完全公式は長いので、参考までに近似式を載せておきます。

kv_th(0.5+b*i) = b*ln(b) - b*ln(2*pi*e) - pi/4 + 1/24/b - . . .

kv_th(s) = -2*k_th(s)　となっています。角度変化は倍ですが、サイクルは同じです。これが不思議なところです。

kv(s)の虚部線は a=0.5 において、k(s)の実零点、虚零点と交わりながら変化します。k(s)の実零点はペアで存在していますが、kv(s)と交わらないほうの実零点がリーマン零点です。ゆえに、kv(s)の角度公式で計算すると、ペアとなっている実零点の場所を特定でき、その近くにリーマン零点があると認定できます。

上記の近似式はｂが大きくなればなるほど誤差が小さくなるので、零点の場所はいくらでも特定できます。しかし、仮定上の零点がある場所だけはペアになっていません。しかも、それを矛盾であると証明できないという問題があります。ですから、実零点の場所はいくらでも特定できますが、どこのペアが壊れているかは判らないので、仮定上の零点の場所を特定することはできず、矛盾を指摘することもできません。





■　　　　　　k(s)　を微分する


複素数は　s=a+b*i という形になっているので、aについての微分と、bについての微分があります。また、方向もあるので、左右の微分、上下の微分もあります。さらに言うと、その点の周り360度すべてで微分係数の計算が可能です。なぜなら、微分係数とはその点における傾きを意味しているからです。それはそれとして、左右、上下を合わせると、合計4種類の微分式があることになります。

微分式を求めることはかなり面倒ですが、できないわけではありません。その4種類の微分式は　ver20 に載せてあります。かなり複雑で、相互に関係しているようには見えません。しかし、零線図を描いてみると、なんとaについての実部微分零線とbについての虚部微分零線が非常によく似ていることに気が付きました。そして、さらに分析したところ、両者は同じものであることが判りました。計算上一致するのでは証明の根拠に使えないので、式の内容から比較したところ、0 < a < 1　で一致することが証明できました。また、f(s) = a0 + a1*s +a2*s^2 + ... という一般式でも証明できました。

つまり、一般の複素関数において、a方向の実部微分式とb方向の虚部微分式は一致するということです。また、a方向の虚部微分式とb方向の実部微分式はマイナスを介して一致しています。この証明は　ver20 に載せてあります。

この現象のことを命名したいと思ったのですが、上手に表現できないので、仮に「微分係数一致の法則」と呼ぶことにします。

a方向の実部微分零線とb方向の虚部微分零線は結局同じ線となります。そして、この線は実零線の上下のふくらみの先端を通り、虚零線の左右のふくらみの先端を通ります。a方向の虚部微分零線とb方向の実部微分零線は同じ線ですが、これは実零線の左右のふくらみの先端を通り、虚零線の上下のふくらみの先端を通ります。（ver20　第6部参照）

この法則を使って、実零線と虚零線で囲まれた空間（閉鎖空間）は存在しないことが証明できます。つまり、実零線と虚零線で囲まれた図形には必ず上下のふくらみの先端、もしくは、左右のふくらみの先端があります。そこは実部零線か、虚部零線のどちらかの通り道になるのですが、反対側の先端に向かう途中に実零線なら虚零線、虚零線なら実零線があるので、それを通り抜けられないという矛盾が生じます。ですから、閉鎖空間（特異点のある場合を除く）は存在できません。


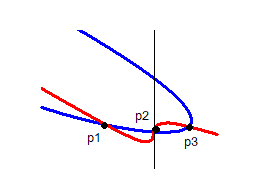
具体例を挙げて説明しましょう。右図の場合、実零線横Ｕ字形の内部に３つの零点が出来ています。青線と赤線で囲まれた閉鎖空間が２つ発生しています。この線上に特異点はありません。ですから、p2右側にある赤線上側頂点から閉鎖空間内部に入ってくるa方向の虚部微分零線は青線の左右の頂点しか通れないので、出口がなくなり、線が途切れるという矛盾が生じます。

この法則により、ほとんどの零線図で仮定上の零点が発生しないことが証明できます。



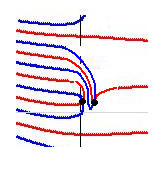
とは言うものの、わずかですが、証明から漏れる図形があります。ひとつ上にある実部横Ｕ字形が下に降りてくる形の場合、閉鎖空間を作らずに仮定上の零点が横に並びます。

一見してこのような形になるはずはないと思える形ですが、証明としては、こういう事例も取り上げなければなりません。

ver20 では、a=0.5上の実零線と虚零線のサイクルが、他のところではkv(s) と一致しているのに、ここだけ変化することを矛盾と捉えて証明としました。「証明としてはこれで充分ではないか」という思いは今でもありますが、角度変化の公式はありますが、サイクルが一致することの証明はできていません。そう言われるとそうかもしれないと思ったので、別の証明に取り組んだ結果、ver64まで来てしまったということです。





■　　　　　　k(s)の拡張形を使う


実部横Ｕ字形がふたつ横に並ぶのはあり得ない形に思えるのですが、証明するのは大変です。角度を変えると零線が変化し、仮定上の零点がある場合、異常な動きをします。しかし、これを矛盾と指摘する論理がありません。伸びたり、縮んだり、歪むことは矛盾ではなさそうです。トポロジーと同じ構造をしているように見えます。

当初、そのことが判らず、零線同士の組み換えは矛盾と言えるのではないかと考えましたが、実際に起きていることがわかり、驚きました。よくよく調べてみると、これは良く起こる現象のようです。

k(s)を複雑にすれば矛盾が見つかるだろうと思って、k(s)*k(s) とか、ベルヌーイ数に変換した　-s*k(1-s)　などを分析してみました。もともと変な形ですから、どのような拡張形にしても矛盾らしきものが見つかります。しかし、矛盾であるとの証明ができません。


零点が横に並ぶ形であっても矛盾とはいえそうもないので、逆に零点が並ぶ関数を作ってみようと思い立ち、作った関数が or(s) です。これは　or(s) = k(a+0.25+b*i) * k(a-0.25-b*i) となっていて、a=0.5の両側0.25の距離のところに零点が出来ています。実際に存在する関数ですから、矛盾はありません。

ただ、ここで気を付けるべきことは、この関数が微分係数一致のない関数であることです。一致がないので、閉鎖空間を作ることができます。






■　　　　　　微分係数の一致の法則


微分係数一致については、すでに説明したように、a方向の実部微分係数とb方向の虚部微分係数が等しくなる現象のことです。この現象はほとんどの複素関数で成り立ちますが、一部、一致しない関数があります。それが or(s) などです。これは　f(s) = a0 + a1*s + a2*s^2 + .... と表記できない関数です。k(s)　の　s=a+b*i のa, b を別々に動かすと、一致の壊れた関数になります。

この関数では、閉鎖空間が発生しても矛盾とは言えなくなるので、証明には向きません。しかし、面白いところもあるので、いくつかトライしてみましたが、結果は失敗でした。

リーマン証明は横に置いておいて、研究するに値する関数だと思います。






■　　　　　　k(s)の式を分解する


零点がa=0.5上になくても矛盾とは言えないので、もし証明ができるとするなら、連続性がどこかで壊れることだと考え、k(s)の式を分解して、k_p3(s) という関数を考案しました。

k_p3(s)は、k(s)が無限計算式なので、その手前の関数ということです。

k(s)の式は先に載せてありますが、zt(s,n)の n と　ber(s,n) のｒを強引に同じ数とみなすことにします。

p3=2 のときは　k_p3(s) = lim_[n→2] { zt(s,n) + ber(s,n) }
かつ、
ber(s,n) = Σ_[r=0,2] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

ということです。

これでも連続にはなりませんから、もうひと工夫します。この説明は長くなるので、ver60を参照してください。

とにかく、仮定上の零点がある場合、k_p3(s) の段階から何らかの影響があるわけで、その影響のもとに連続した変化を遂げると、どこかに矛盾が生じるのではないかと予想をして分析を進めました。

しかし、複雑な変化を遂げる割には、矛盾というものは発生しないことが判明し、この証明も失敗に終わりました。







■　　　　　　今後の方向性



まだトライしてない分野も残っています。四元数とか、行列とか、積分、逆関数、その他、次元を上げた関数などです。これらを分析すると矛盾が見つかるかもしれません。また、まったく発想を変えた証明もあり得ます。ですから、まだ証明の可能性は残っていると思います。しかし、今後は矛盾がないことを証明することも視野にいれて分析をする必要があると思います。

矛盾がないということの証明はどうやったらよいかイメージがわきません。まずは、どうやって証明するのかを検討することから始めることになるでしょう。先は長そうですね。








■　　　　　　無矛盾性の証明は難しい


無矛盾性の証明には一度トライしています。（ver40）　しかし、証明の形をとることさえできませんでした。「すべての可能性」を検討したうえで、そのどれもが証明できないことを示せば良いのですが、「すべての可能性」がどこまでなのかを確定させることは至難の業と言えるでしょう。

おそらく、無矛盾性の証明は、矛盾を見つけ出すことと同程度に難しいと思います。とは言うものの、何事もあきらめてはなりません。手あたり次第やってみると、道が開けることもあります。


単純に考えると、証明ができないのも当然という気がしてきます。そもそも、k(s)は規則性のない関数で、素数と連動している関数です。素数には法則がありません。ですから、k(s)にも法則はありません。証明というのは、矛盾を指摘するための根拠が必要です。ところが、k(s)にはその根拠となる法則がないのです。・・・もっとも、全くないわけではありません。「もし仮定上の零点があるなら、それは　a=0.5軸から等距離のところに発生する」とか、「a=0.5上の複素角変化の公式が存在する」などです。しかし、これだけでは今のところ証明は完成しません。別の法則が必要ですが、まだ見つかっていないし、今後も見つからない可能性があります。ですから、証明は難しいのです。







■　　　　　　k_r(s)に矛盾があるか、k_th(s)に矛盾があるのか。



仮定上の零点がある場合、そこに何らかの矛盾を指摘できなければ証明は完成しません。もし、矛盾を見つけることができるなら、問いかけるべきことは、その矛盾が k_r(s) に由来するものか、k_th(s)に由来するものか？　ということです。

k_r(s)とはk(s)の絶対値関数のことです。k_th(s)とは複素角関数のことです。たとえば、(1,10)の点におけるk(s)の値は　(1.3902873E0, -1.0978515E-1) です。この点の絶対値は　1.3946152E0　で、角度は-7.8802280E-2　です。極座標表示すると　r*(cosθ+i*sinθ) となります。このｒが絶対値で、これを答えとする関数が絶対値関数　k_r(s) です。θが角度で、これを答えとする関数が複素角関数です。

絶対値関数と複素角関数は相互依存しているように見えますが、式としては完全独立で、別々の関数を持ってきても、極座標表示は成り立ちます。k(s)の場合も、たまたま　k_r(s) であり、k_th(s) であるともいえます。では、もし、仮定上の零点に矛盾があったとき、その原因は k_r(s) にあるのでしょうか。それとも、k_th(s)にあるのでしょうか。ふたつが相互独立なら、両方に矛盾があるというより、どちらかに原因があると考えるべきです。

私の当初の予想では、k_th(s)は矛盾の原因にはならないと考えました。なぜなら、リーマン零点は、値としては (0,0) ですが、前後から連続していると考えると、その点における複素角を計算できます。複素角θが存在するとすると、　(cosθ+i*sinθ)　ですから、実部か虚部のいずれかは必ず値を持ち、(0,0)になることはありません。零点とは絶対値ｒが零であるから発生するものだと結論付けました。仮定上の零点の発生は角度に関係なく、k_r(s)が０であれば、そこが零点になるわけです。矛盾を探すなら　k_r(s)を分析しなければならず、k_r(s)に矛盾がないことを証明できれば、リーマン証明が不可能であることの証明になると考えました。

ところが、みごとその予想は外れてしまいました。絶対値ｒを１に固定し、複素角だけの零線図を描いてみたところ、なんと　k(s)　と同じ零線図が出来上がったのです。リーマン零点の場所が零点になっています。そんなはずはないと思い、a=0.5のｘｙ図を描いたところ、k(s) とは別の図が現れ、そこには零点はありませんでした。こういう困ったことが起きてくるのが数学の恐ろしさ・・・、面白さです。

プログラムミスがあるのだろうと考え、a=0.4のｘｙ図を描いてみると、今度は、零線図と同じ場所に実部零点、虚部零点が現れました。a=0.49 にも零線図と同じ場所に実部、虚部零点がありました。プログラムは間違ってないと判断できます。すると、a=0.5上では、見かけの実零線、虚零線の交点はありますが、その交点は絶対値１、複素角もある普通の複素数ということになります。

この見かけ上の交点がa=0.5上にしかないと証明できれば、リーマン証明は完成することになります。しかし、残念ながら、k_p3(s)で、同じように、絶対値１で角度だけ変化させる零線図を描いたところ、k_p3(s)の図とまったく同じになりました。a=0.5でない場所に見かけ上の零点が現れています。この見かけ上の交点はどこにでも発生しうるものであることが判ります。すると、リーマン証明はできないということになります。

もし、仮定上の零点で矛盾が生じるなら、複素角関数が原因で発生することになり、絶対値関数は関係ない可能性が大です。しかし、複素角関数ではどこにでも交点ができるようで、k(s)の場合だけ矛盾であることを指摘する材料は今のところ見つかりません。


ということは、k_r(s)には仮定上の零点があっても矛盾は生じないと断言してよいということでしょうか。そのあたりのことはまだ何とも言えません。

そもそも、もっとも大きな問題は、ver40 で指摘してあるように、仮定上の零点が存在する関数が存在していることです。その関数は　k(s) ではありません。しかし、存在しているということは、矛盾はないということです。矛盾を探す証明はもはや無意味と言えるかもしれません。矛盾を指摘することではなく、「仮定上の零点のある関数はk(s) ではない」という命題を分析するなら、また別の証明方法を思いつくかもしれません。





■　　　　　　k_p3(s)で証明する


もうひとつ問題提起をしておきます。

証明が出来なければ、より簡単な命題を出して、それを証明して見せることが前進となることがあります。

k_p3(s)は無限関数ではないので、k(s)よりも単純です。p3=2 とすると非常に扱いやすい関数になります。p3=2 の場合、リーマン零点（実虚零点）は　a=0.5上に並んでいるわけではありません。しかし、bが50以上になると零点はすべて　a=0.5軸の右側になり、それが無限大まで続いているように見えます。この「右側にある」ことはリーマン証明の材料にならないので、証明しても意味はないのですが、ためしに証明してみると、なんとか出来そうな気がします。では、実際はどうなのでしょうか。

p3=2 の式を再掲しておきます。


k_p3(s) = zt(s,2) + ber(s,2)　

zt(s,2) = 1 + 1/2^s

ber(s,2) = Σ_[r=0,2] B(r)*(s-2+r)!/r!/(s-1)!/2^(s-1)/n^r

つまり、

ber(s,2) = B(0)*(s-2+0)!/0!/(s-1)!/2^(s-1)/2^0 + B(1)(s-2+1)!/1!/(s-1)!/2^(s-1)/2^1 + B(2)*(s-2+2)!/2!/(s-1)!/2^(s-1)/2^2

ということです。

ber(s,2)はやや長いものの、k(s)よりはずっと扱いやすくなっています。



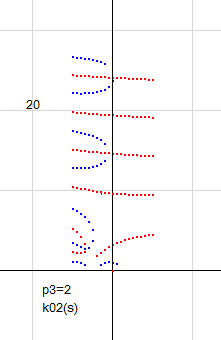
零線図は右のようになっています。

k(s)とたいして違わないようですが、bが増加すると、実虚零点は右側に寄ってきて、すべて a=0.5 軸より右に来ます。常に右側ですから、証明は簡単そうに見えます。

証明方法は　k_p3(s) の部品の中で最大増加要因である　B(2)*s/2!/2^(s-1)/4　を分析して、この絶対値がｂの増加とともに必ずより大きくなることを証明することです。この部分が大きくなれば、k_p3(s)全体の絶対値も大きくなり、a=0.5上の実部虚部波の揺れはより大きくなります。すると、実部線、虚部線は波のサイクルごとにz=0を必ず通過することになります。z=0の上下に波が来るということは、左から張り出してきている実部横Ｕ字形は必ずa=0.5よりも右に来るということであり、虚零線はその間を通っているのですから、実部線と虚零線の交点は必ずa=0.5軸より右に来ることになります。

結構、簡単な証明のように思えます。・・・・ところが、よくよく考えてみると、この証明は間違っています。なぜなら、a=0.5上の実部波、虚部波が一定のサイクルで波打っていることの証明はできていないからです。もし、k(s)の仮定上の零点の場合と同様に、サイクルがひとつ飛ぶような現象が起きているとすると、波の高さは関係なく、零点のひとつはa=0.5より左側に来ることになります。もちろん、そんなことはあり得ないのですが、ありえないことはまだ証明されていません。

結局、p3=2 の時の証明は、k(s)のリーマン証明と同じような問題を抱えていることになります。

k(s)より簡単な式であるp3=2 の式で証明ができないのですから、k(s)での証明にトライして出来ないのは当たり前です。












証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部





表紙に戻る



ご感想、ご質問、ご意見などは、Mailのアドレス（hirokuro303@gmail.com）へお願いします。