リーマン零点が横に並ばないことの証明

ver74　　　　new 2019/12/16



残念がご報告ですが、ver74 証明は失敗しました。ほとんどうまくいっていたのですが、最後の最後で扉をこじ開けられませんでした。

失敗の原因は、zt_dx(s) が象鼻形という形にならないことを証明できなかったことです。逆に言うと、象鼻形という形にならないことを証明できれば証明は完成したということです。そして、象鼻形とは、象の鼻のように長く垂れさがる形で、状況からも、構造からもありえない形です。なんとか証明できるのではと思い、実際、証明できそうな材料はあちこちにあったのですが、残念ながら証明には繋がりませんでした。

毎度のことではありますが、とてもがっかりしています。しかし、これで諦めることなく、次のアイデアを探してみようと思っているところです。

以下、今後の参考のために　ver74β を保存しておくことにします。









リーマン零点は計算上、a=0.5 上に縦に並んでいて、横に並ぶことはありません。しかし、a=0.5 上にないことがあると仮定すると、その零点は a=0.5 から左右対称の場所に横に並んで存在しなければなりません。このことはすでにver20 で証明済みです。ですから、「横に並ばなければ a=0.5 上にある」ことになります。そこで、「横に並んだと仮定して」、そこに矛盾を見つけようとしたのですが、今まではうまくいきませんでした。いつも「今回はうまくいく」との期待と希望のもとにやっているのですが、なかなか難しいものですね。はたして今回はどうでしょうか。うまくいったと思うので公表するのですが、過去の証明も同じように「うまくいった」と思って公表したものばかりですから、だんだん自信がなくなってきました。間違いがあるなら、はやく見つけたいので、見つけた方はご一報いただけると幸いです。


今回取り上げる関数は　qnk(s) と　qnzt(s)　と　qnber(s) です。この３つの関数の関係は

qnk(s) = qnzt(s) + qnber(s)

となっています。名前を見ればわかると思いますが、これは今まで使っていた　k(s) = zt(s) + ber(s) と同じ形をしています。名前に　qn が付いただけです。中身もよく似ています。違いは、全体に　dx^s　が掛けられていることです。こんな小さな変化で証明がうまくいくのかという印象ですが・・・、まぁやってみましょう。

今までの証明でおもに取り上げたのは、有限級数であるところの　k_dx(s), zt_dx(s), ber_dx(s) です。これらは　k(s), zt(s), ber(s) を有限化し、dx まで計算した式を意味しています。これらにも　dx^s　を掛けて、同じやり方で名前を付けておきます。　qnk_dx(s) = k_dx(s) * dx^s　、　　qnzt_dx(s) = zt_dx(s) * dx^s　、　　qnber_dx(s) = ber_dx(s) * dx^s　　　です。

k_dx(s) ,　zt_dx(s),　ber_dx(s) 　の定義はすでに過去の証明で説明してありますが、再度書いておきます。


k(s)　はいわゆるゼータ関数のことです。二重の無限級数の形をしています。ber(s,n) の公式に現れる　r　を n までとして、この n　の表記を dx 変更したものが上記の式です。最初に　n, r で定義した式は次のものです。

k(s) = lim_[n→∞] { zt(s,n)+ber(s,n) }

zt(s,n) = Σ_[r=1,n] 1/r^s

ber(s,n) = Σ_[r=0,n] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

zt(s,n) と　ber(s,n)　の詳しい説明は　ver20 を参照してください。

r→n　とした　ber(s,n)　を zt(s,n) と一緒にし、さらに　n→∞　にしたものが　k(s) です。過去の証明で n を実数として証明にトライしたことがありました。そのとき、n を　dx　と書き変えました。今回、dx を自然数に戻したのですが、書き直すのは面倒なので、記号はそのままにしてあります。ご了承ください。

k_dx(s), zt_dx(s), ber_dx(s) は　それぞれ dx まで計算したものといいう意味です。zt_dx(s) と　zt(s,n) は同じことです。ber_dx(s) も　ber(s,n) と同じです。k(s) と　k_dx(s) は少し違います。k_dx(s)= zt_dx(s) + ber_dx(s) となっています。

さて、この式全体に　dx^s を掛けるということですが、これにより　ber_dx(s) は少しだけ簡略化されます。ber_dx(s) = Σ_[r=0,dx] B(r)*(s-2+r)!/r!/(s-1)!/dx^(s-1)/dx^r 　という式の分母に　dx^(s-1) というのがあります。この　dx^s　が消えるので、qnber_dx(s) = Σ_[r=0,dx] B(r)*(s-2+r)!/r!/(s-1)!/dx^(r-1) 　となります。

qnzt_dx(s) = zt_dx(s) * dx^s 　ということなので、qnzt_dx(s) = (dx/1)^s + (dx/2)^s + (dx/3)^s + ... + (dx/(dx-1))^s + 1　　　となります。

qnk_dx(s) 　については、式の簡略化はありません。すなおに　dx^s　を掛けるだけです。


これらの新しい関数にもそれぞれの零線図があります。また、それぞれの全体構造があります。dx^s を掛けただけなのですが、決して小さくはない違いが生じています。

零線図の種類と、説明すべき形の数はかなり多いのですが、まずは証明の手段となる符号計算などの説明を先にし、証明に関係する関数の内容を説明し、必要なところは証明し、それから、仮定上の零点を持つ場合の零線図、そして、矛盾点の指摘へと進めてゆきたいと思います。






■　　　　　　零線図の符号計算（足し算）


仮定上の零点を持つ零線図は計算できません。しかし、なにか手がかりがないと証明は出来ないので、零線図を描くためのやり方として符号計算という方法を導入します。これは零線図を重ね合わせることにより、そこに出来る交点と区域の符号変化を計算します。まずは、このやり方を一般的に説明しますが、すでにわかっている人は、ここは飛ばして、仮定上の零線図の計算に進んでください。

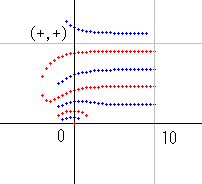
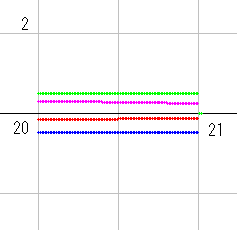
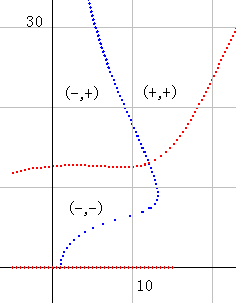
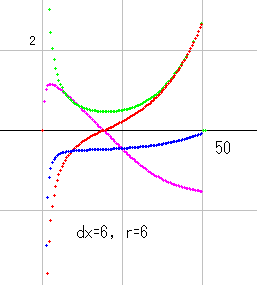
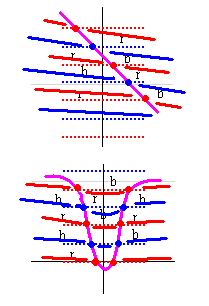
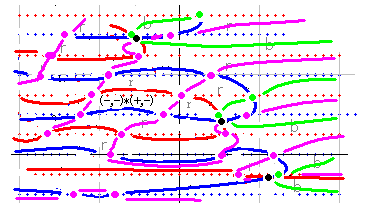
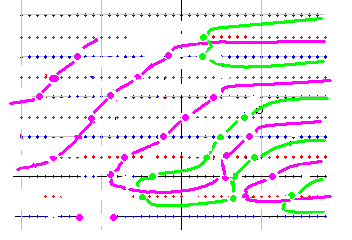
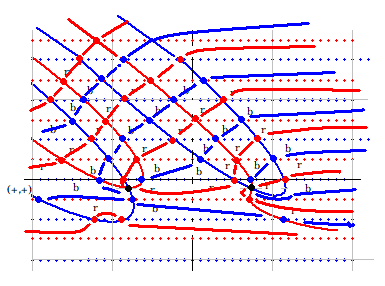
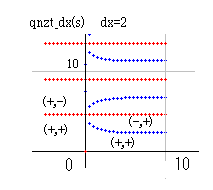零線図の足し算を説明するために、qnzt_dx(s) の零線図を取り上げることにします。qnzt_dx(s) は　先にも言いましたように　zt_dx(s) * dx^s　で計算します。右図は dx=2 で、b=15 までの図です。

実零線が青、虚零線が赤で示されています。零線が作る区域の符号は　(10, 0) の上側が (+,+) です。これは計算により求めます。その上の青線の上側が (-,+) で、その上の赤線の上側が (-,-) です。以下、同じやり方で符号が決まります。

青・赤線以外の線は区域判定では無視されるので、ご注意ください。




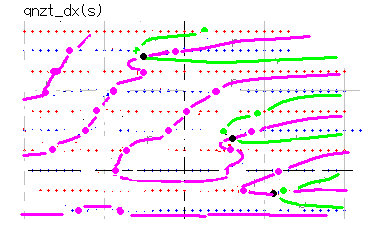
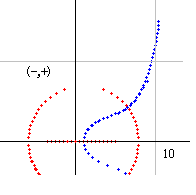qnber_dx(s) の図は右図のようになります。dx=2　の図です。

(10, 0)　の上側は (+,+) になっています。青線の反対側は (-,+) になります。









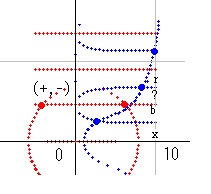qnzt_dx(s) と qnber_dx(s) を足すということは、ふたつの零線図を重ねて符号足し算をすることです。

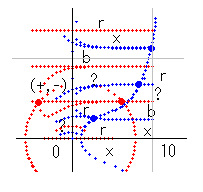
s=a+b*i とすると、青線とは　a=0 の点が集まった線ということです。赤線とは　b=0 の線です。青線と青線の交点とは (a+b*i) + (c+d*i) = (a+c) + (b+d)*i　、a=0, c=0 　なので、0 + (b+d)*i となります。つまり、この点を新しい青線（実零線）が通ることを意味しています。ここに青点を打っておきます。赤線と赤線の交点とは　b=0, d=0 なので、(a+c) + 0　で、この点を新しい赤線（虚零線）が通ることを意味しています。ここに赤点を打ちます。

青線と赤線の通り道は決まっていて、どこを通るかは符号計算により決まります。a,b,c,d を正の整数とすると、(10, 0) の上側はどちらも (+,+) なので、(a+b*i) + (c+d*i) = (a+c) + (b+d)*i となり、実部も虚部も必ずプラスになります。つまり、青線も赤線も通れない区域なので　ｘ区域　と判定されます。その上の青線上側は　qnzt_dx(s) が (-,+)、qnber_dx(s) が (+,+) なので、(-,+)+(+,+) = (?,+)　となり、実部が零になる可能性を持つ区域となります。つまり、実零線が通ることのできる区域なので、blue の頭文字をとって、ｂ区域と呼ぶことにします。さらにその上の赤線上側は　(-,-)+(+,+) = (?,?) となり、実零線も虚零線も通ることができます。これを　？区域と書くことにします。その上の区域は　(+,-)+(+,+) = (+,?)　となり、虚零線が通ることのできる区域となります。red の頭文字をとって　ｒ区域と呼ぶことにします。

この計算をすべての区域で実行するのが符号計算です。しかし、実際に計算しなくても、いくつかの区域が判明すれば、あとはある法則を使うと簡単に判定できます。

ｂ区域の青線の反対側は　ｘ区域。ｂ区域の赤線の反対側は　？区域。ｒ区域の青線の反対側は　？区域。ｒ区域の赤線の反対側は　ｘ区域。

？区域と　ｘ区域の周りの区域は上記の原則を応用するとすぐに判定できます。

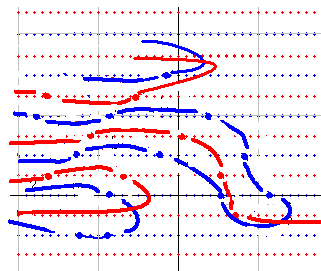
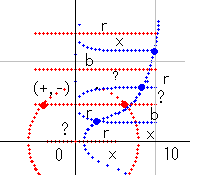その原則を使って計算した結果が右図です。

（黒線と灰色線は無視されます。）










qnk_dx(s) = qnzt_dx(s) + qnber_dx(s) なので、qnzt_dx(s) と qnber_dx(s)　を符号足し算した結果は　qnk_dx(s)　の零線図になります。

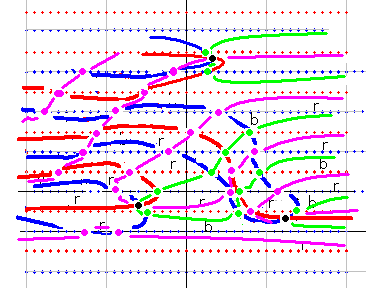
右図は k_dx(s) * dx^s　を実際に計算した結果描かれた　qnk_dx(s) 図ですが、先の重ね合わせの図と右図を比較すると　青点を qnk_dx(s) の実零線が通り、赤点を虚零線が通っていることが確認できます。通り道も区域計算通りであることが確認できます。





念のため、qnk_dx(s) を重ねた図を載せておきます。

qnk_dx(s)　の青線が青点を通り、赤線が赤点を通っていることが確認できます。区域も正しく判定されていることが確認できます。







■　　　　　　符号計算の掛け算


零線図を重ねた時の掛け算は区域ごとにその符号を検討することで計算可能になります。qnber_dx(s) と　1/dx^s を使って説明します。qnber_dx(s) = ber_dx(s) * dx^s　なので　ber_dx(s) = qnber_dx(s) * 1/dx^s　となっています。


掛け算の符号計算は、(a+b*i)*(c+d*i)を調べることで可能になります。A*B=B*A　なので、符号の組み合わせは10通りとなります。a,b,c,d　をプラス実数とします。(a+b*i) は　(+,+) 、(a-b*i) は　(+,-)　と表記します。(a+b*i) * (c+d*i) = ac-bd + (ad+bc)*i　で、(ac-bd) はプラスにもマイナスにもなるので　？　と表記します。ですから、符号計算の式は　(+,+)*(+,+) = (?,+)　となります。(a-b*i) * (c+d*i) = (ac+bd) + (ad-bd)*i　の場合は　(+,-)*(+,+)　となり、答えは　(+,?) です。これを種類ごとにまとめると、

(+,+)*(+,+) = (?,+)　　　(+,+)*(+,-) = (+,?)　　　(+,+)*(-,+) = (-,?)　　　(+,+)*(-,-) = (?,-)　　　(+,-)*(+,-) = (?,-)　　　(+,-)*(-,+) = (?,+)　　　(+,-)*(-,-) = (-,?)　　　(-,+)*(-,+) = (?,-)　　　(-,+)*(-,-) = (+,?)　　　(-,-)*(-,-) = (?,+)

これで全部です。

実零線と実零線の交点は　(0+b*i)*(0+d*i) = (-bd+0*i) なので、必ず虚零線の通り道になります。また、虚零線と虚零線の交点も　(a+0*i)*(c+0*i) = (ac+0*i)　なので、新しい虚零線の通り道になります。ここには赤点を打ちます。実零線と虚零線の交点は　(a+0*i)*(0+d*i) = (0+ad*i)　もしくは、(0+b*i)*(c+0*i) = (0+bc*i)　なので、新しい実零線の通り道になります。ここには青点を打ちます。

以上の法則を実際の零線図で確認してみましょう。

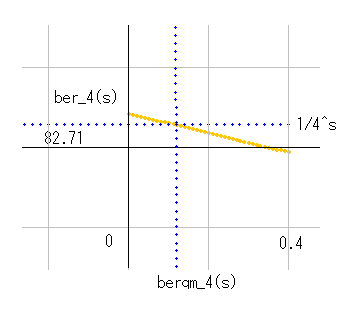
dx=4 のとき、1/dx^s の実零線は　b=81 付近を通る横直線（青線）です。それに対して、qnber_dx(s) の実零線（青線が上から下ってきます。その交点を　ber_dx(s) の新しい虚零線）（橙線）が通ります。右図を見ると、計算通りになっていることが確認できます。（図の中で　berqm と書かれているのは　qnber　のことですので、ご了解ください。）

実零線と虚零線の交点は　ber_dx(s) の新しい実零線が通ります。この図は省略します。


さて、上の図がかなり拡大されていることからわかるように、普通の縮尺では 1/dx^s と　ber_dx(s)　がほとんど重なってしまい、どこが交点かはっきりしなくなります。ゆえに、今後の作図においては、交点などをはっきりさせるために、手書きの図を使うこともあるので、ご了承ください。






■　　　　　　a=0.5 上の角度変化


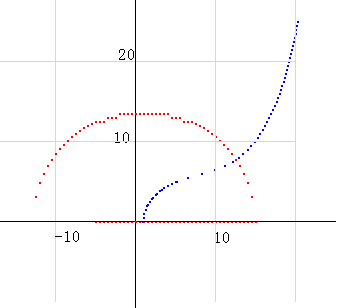
k(s) の　a=0.5 上の角度変化は公式があるので、証明の根拠として使うことができます。ver29　■１０の６■　、もしくは、「私の発見した数学公式・派生した公式（その２）」を参照してください。変化は図上では右肩下がりで、角度としては常に減少です。

完全公式は長いので、近似公式を再掲しておきます。

k_θ(0.5+b*i) = -1/2 * { b*ln(b) - b*ln(2*pi*e) - pi/4 + 1/24/b + . . . }

角度は　2*pi ごとに同じ場所に戻ります。ですから、角度１と 2*pi+1 は同じ数とみなされることにご注意ください。1-2*pi も同じです。誤差については、完全公式に近づけて計算するとすぐになくなります。

dx^s の角度変化は　b*ln(dx) と公式化できます。図としては右肩上がりの直線となります。

k_dx(s) の角度公式はありませんが、dxが巨大化するとk(s) に収束するので、同じものとして使うことができます。qnk_dx(s) も、k(s) と dx^s の公式から計算することができます。qnk_dx(s) は　k_dx(s) と　dx^s の掛け算なので、角度は足し算となります。k(s) は傾きがマイナスの角度で、dx^s はプラスなので、qnk_dx(s) の角度がどうなるかは分析が必要です。dx が大きくて　k(s) に収束しているという条件で、qnk_dx(s) の角度公式は以下のようになります。

qnk_dx_θ(s) = b*ln(dx) - 1/2 * { b*ln(b) - b*ln(2*pi*e) - pi/4 + ... }

仮定上の零点がある場所ではｂが定数となるので、dx がｂより増えると角度が　b*ln(dx) に近づきます。単純増加なので、実部波と虚部波は交互にz=0 を通過することになります。


qnber_dx(s)　は　 Σ_[r=0,dx] B(r)*(s-2+r)!/r!/(s-1)!/dx^(r-1) という式なので、複雑すぎて説明は容易ではありません。仮定上の零点がある場所ではｂが固定されるので、定数とみなすことができます。dx は増加し続ける数なので、1/dx(r-1) の部分が大きく影響して、ｒが大きいところではすべて零に近くなります。ですから、ｒが　 0, 1, 2, ...　などの少ないところの形が最後の qnber_dx(s) の形を決めることになります。これについては、あとで詳しく説明し、必要なところは証明します。

qnzt_dx(s) の角度は、公式はなく、また、一定でもありません。しかし、仮定上の零点がある場所ではある形を取ることが証明できます。その証明は後で載せますが、その形の場合の角度変化を調べることは可能です。







■　　　　　　a=0.5 上の実部線、虚部線の値


ver74 証明では　a=0.5 上のｙｚ図を使った足し算・引き算が必要になります。これはいままで取り上げてなかったテーマです。そこでまずは計算可能なところで、足し算・引き算がどのように行われるかを説明します。

零線図とはｘｙｚ座標で考えると　z=0 のときの　ｘｙ図ということです。a=0.5 軸上の図は　ｘｙｚ座標でいうと　ｙｚ図となります。ｙとはｂのことで、ｂ上の値がｚの値になります。そして、複素関数の場合、ｚ上の値に実部と虚部のふたつがあるという特徴があります。ここで分析するのは ｚ上の実部の足し算・引き算、虚部の足し算・引き算です。

qnzt_dx(s) = qnk_dx(s) - qnber_dx(s) の式が今回、ｙｚ座標での引き算が必要になる式です。仮定上の零点がある場所では、普通の計算ができないので、座標計算を使うことになりますが、まずは計算可能な場所で、ｙｚ図の足し算・引き算のやり方を実践しながら、その結果と計算結果を比較し、その有効性を確認したいと思います。

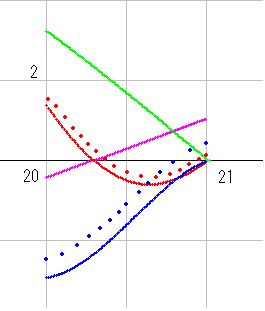
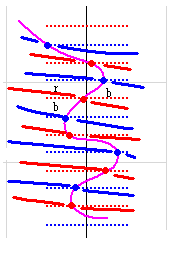
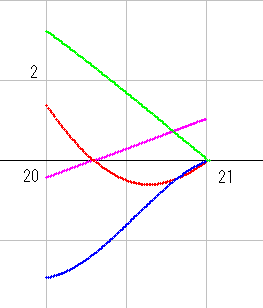右図が　qnk_dx(s) の　a=0.5 上のｙｚ図です。dx=8 となっています。

実部波が青線、虚部波が赤線です。絶対値が緑線、角度が桃線ですが、このふたつは今回は使いません。
















右図は　qnber_dx(s) のｙｚ図です。ほとんど直線なので図上での計算が楽です。

qnk_dx(s) から qnber_dx(s) を引くというは、線上の値を引くということです。qnber_dx(s) の実部線・虚部線はマイナス部分を走っているので、図ではプラスすることになります。qnk_dx(s) から　qnber_dx(s) を引くとは、この図の場合は線を上にずらすことなので、少し上に点で目印をつけておきます。








その結果が右図です。





















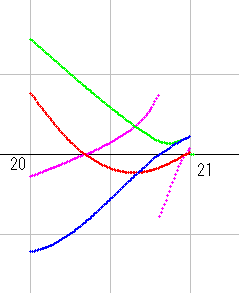右図は　計算によって求めた　qnzt_dx(s) の図です。dx=8 a=0.5 b=20 です。

先の図と重ねると、青線・赤線がだいたい点線上に来ていることがわかります。

これで、実部・虚部線図における引き算のやり方が正しいことが確認できました。







掛け算・割り算のやり方は、証明では使わないので、説明は省略しますが、絶対値を掛ける（割る）のと、角度を足す（引く）作業をして、その結果に合わせた実部と虚部を計算すると答えが出てきます。







■　　　　　　k(s) の構造と零線図


k(s) については、すでに ver20 で詳しく説明しているので、そちらを参照してもらいたいと思います。証明の基本となる関数で、これを前提にしないと話が始まりません。

一応、零線図を再掲しておきます。




































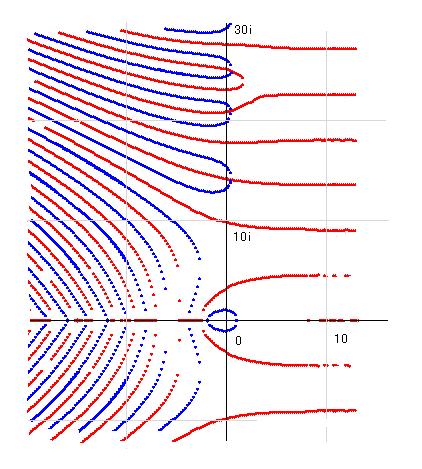
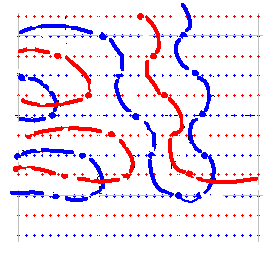
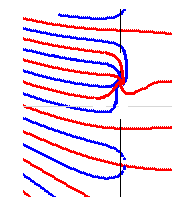仮定上の零点があるとすると、その場所の零線図を想定することは可能です。ただ、それを上記の図に書き込むことは困難です。あまりに形が悪すぎるからです。しかし、ためしにあえて描くとすると右図のようになります。そういうことはありえないという形ですが、その「ありえない」ことを証明するのがリーマン証明です。

この図のままでは、証明の手順説明さえ出来ないので、歪みを修正して、見た目にわかりやすく直したのが次の図です。








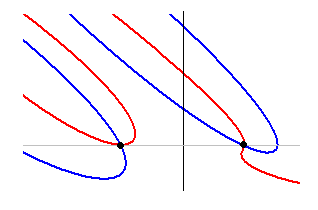想定しうる形はその他、いくつかありますが、まずはこの形で矛盾が生じることを証明するのが今回のver74 の目標です。この証明の論理が正しければ、そのやり方を他の形にも適用して、すべての形について矛盾が生じることを示す予定です。












k(s) と　k_dx(s) の関係は微妙なところがあるので、説明しておかなければなりません。 k(s) = lim_[n→∞] { zt(s,n)+ber(s,n) }　で定義されているので、理論上は　n を無限大にしなければ　k(s) になりません。しかし、n　を無限大にしなくても、増加させるだけで、零線図のｂが小さいところから順次収束が進み、零線図を描くのに問題ないレベルになります。ｂが大きいところではまだ収束していませんが、n　をさらに増やすとやがてそこも収束します。この　n を ver74証明では　dx と表記しています。ですから、dx　をある程度大きくするなら、その収束した範囲では　k(s) と k_dx(s) は同じ関数となります。仮定上の零点がある場所は　ｂが有限なところなので、仮定上の零点がある場所を収束させるためには、dxを無限大にする必要はありません。かなり大きな数と想定されますが、その大きな　dx で、仮定上の零点は収束しているのですから、その場所では　k(s) と　k_dx(s) は同じ関数とみなされます。








■　　　　　　qnk_dx(s) の構造と零線図


qnk(s) という名称をすでに紹介していますが、qnk(s) = k(s) * dx^s という定義は良いとしても、qnk_dx(s) = k_dx(s) * dx^s という関数もあります。そして、先に述べたように、k(s) と　k_dx(s) は実質的に同じ関数なので、この両者は実質的に同じものとなります。しかし、qnk(s) は　dx^s を含むので収束しません。ですから、説明のためには　qnk_dx(s) を使うことになります。

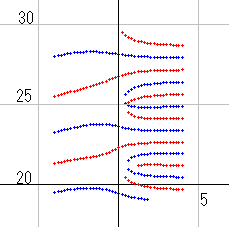dx=8 としたときの零線図が右図です。

実零線と虚零線の幅が狭いので、少し拡大してあります。

k(s) とかなりの違いがあります。横Ｕ字形が右に向かわず、左に向いています。また、実零線の中には左無限まで到達するのがあります。








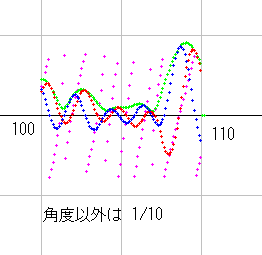
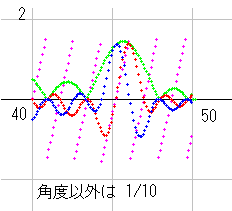dx=16 としたときの　a=0.5 上のｙｚ図です。青が実部波、赤が虚部波、緑が絶対値、桃が角度です。波の高さが高いので、角度以外は　1/10 にしてあります。k(s) と同じ場所にリーマン零点が出来ています。また、零点のない場所にも波があります。













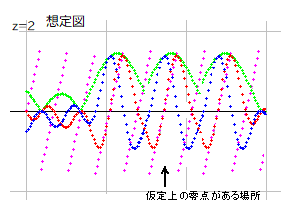仮定上の零点がある場所のｙｚ図を想定することができます。仮定上の零点は a=0.5 上にはないので、ｙｚ図には零点は現れません。零点のない場所の波と同じ波になります。ですから、この図を見ても、ここに仮定上の零点があるとは判らない構造になっています。もちろん、零線図を見ると、そこにリーマン零点があることが確認できます。その図はのちほど、証明の中で載せることになります。









■　　　　　　qnber_dx(s) の構造と零線図


qnber_dx(s) は　ver74 証明の核となる関数なので、詳しく説明します。

qnber_dx(s) = ber_dx(s) * dx^s 　ですが、式の内容を見たほうがよくわかります。

ber_dx(s) には　dx^s で割るところがあるので、dx^s を掛けると、それが消えて、よりシンプルな式になります。

qnber_dx(s) = Σ_[r=0,dx] B(r)*(s-2+r)!/r!/(s-1)!/dx^(r-1)

とは言うものの、シグマ付きの総和計算なので、この式をさらに細分して、ひとつひとつ分析することにします。

ひとまず、全体の qnber_dx(s) を見てみましょう。

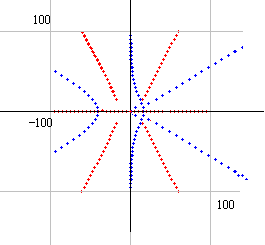
dx=4　とすると　右図のようになります。

零線の数が少ないので、今までの零線図とかなり雰囲気が異なります。


















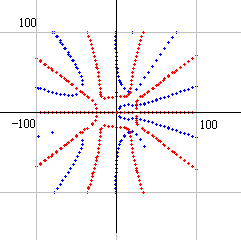
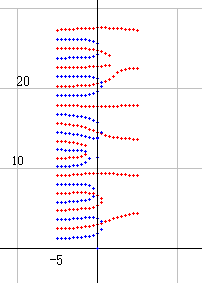
拡大して　a=-100 から　a=100 までを描くと、右図のようになります。
















dx　を増やすと零線の数はどんどん増えます。

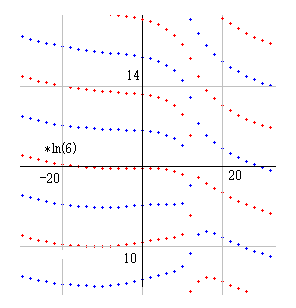
dx=6 のときが右図です。無限大に繋がる線を数えると　２０本になります。この数は　dx により決まっています。dx=8 だと　２８本、dx=10 だと　３６本で、(dx*4-4)　の関係です。

(0,0) に近いところを走る実零線は　(1,0) から出発していて、0 < a < 1 　には虚零線、その上に実零線が走っているのが確認できます。









qnber_dx(s) については、零線図だけでなく、a=0.5 上のｙｚ図も重要になります。

右図は　dx=6 のときの　a=0.5 の図です。虚部波は上方に上りますが、実部波はマイナスから０に向けて動きます。この図からわずかに外れていますが、b=50 より少し上に実部零点があります。dx を増やすと、実部零点は右にずれます。dx をさらに増やすと、零点もさらに右に移動します。dx は最後には無限大になる数なので、この零点も無限大にまで移動しますが、その無限大になる前に仮定上の零点のある場所を通過します。すると、仮定上の零点のある場所の　qnber_dx(s)　の　a=0.5 上の値は必ずマイナスで、値も０に近いと言うことになります。

この事実は証明の材料となるので、あとで厳密に証明する予定です。







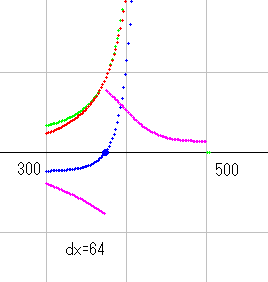dx=64 とすると、青零点がかなり右に寄ることが確認できます。

このまま、単純に右に移動し、同じｙｚ図が得られるかと思ったところ、dx=128 で別の図になることがわかりました。













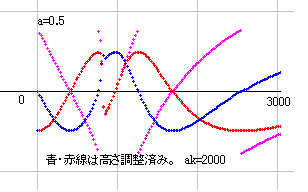dx=128, a=0.5 のｙｚ図です。

実部、虚部とも、巨大な数になるので、絶対値で割っています。桃線が角度線です。実部、虚部ともに、まっすく無限大に向かうのではなく、波となって運動することが確認できます。誤差が生じないよう、計算精度　ak=2000 としてあります。

つまり、実部零点は　b=700 あたりに存在しますが、そのあとも、b=1200 あたりで零となり、b=2500 あたりでまた零となっています。実部零点はいくつもあるようです。しかし、最初の零点が　dx の増加とともに右に移動することは間違いありません。その証明はあとで載せることになります。

dx=128 で、b=1000 あたりから実部線が波になるのは、k(s) が収束しないからです。b=1000 でも収束するほど dx が増加すると、b=1000 の実部値がマイナスになることは　qnber_dx_r(s) の　r=2 のところで証明しています。そちらを参照してくださ。








■　　　　　　qnzt_dx(s) の構造と零線図


qnzt_dx(s) = zt_dx(s) * dx^s ですが、qnzt_dx(s) = qnk_dx(s) - qnber_dx(s) でもあります。qnzt_dx(s)　を求めるのにふたつのやり方があるというのが、このver74 を思いついたきっかけですが、それがただちに証明に繋がったわけではありません。しかし、これを使って、証明の材料が見つかったのですから、qnzt_dx(s) はとても重要な関数であることに変わりありません。

それはそれとして、qnzt_dx(s) の零線図を載せておきます。


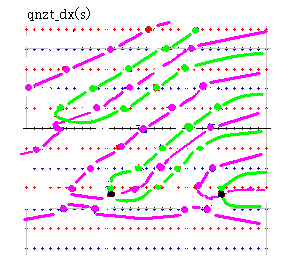
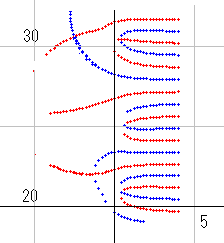dx=8　のときの零線図です。右側から横Ｕ字形が伸びてくるのは　qnk_dx(s) と同じです。零線同士の幅も同じです。やはり、dx^s を掛けた影響は非常に大きいといえます。













a=0.5 上のｙｚ図も重要なので、載せておきます。右図は　dx=16 で、b=100 のものです。

リーマン零点はありませんし、角度も直線ではなさそうです。波の揺れ方も法則性があるようには見えません。しかし、実部波、虚部波と z=0 との交点は交互におきています。










■　　　　　　ber_dx(s) の構造と零線図


ber_dx(s) は、もともと　ber(s,n) で定義されていた基本的関数ですが、qnber_dx(s) / dx^s として説明したほうがわかりやすいので、後回しになりました。

式の内容を見ても判るように、ber_dx(s) よりも　qnber_dx(s) のほうが単純です。その　qnber_dx(s) を　dx^s で割ると　ber_dx(s) になります。

ber_dx(s) の式を再掲すると、

ber_dx(s) = Σ_[r=0,dx] B(r)*(s-2+r)!/r!/(s-1)!/dx^(s+r-1) 　となります。

ber_dx(s) の零線図は、単純なわりに複雑で、全体を説明するのは結構面倒です。

dx　を増やすと、幅が狭くて図にならないので、b　に　10/ln(dx) を掛けて上下を広くすることにしました。

右図は、dx=4 で、上下の幅に 10/ln(6) を掛けたものです。横が 40 、縦が　4　ですから、、0 < a < 1 　では、ほとんど横線であることが判ります。

この「横に流れる」という現象は証明の根拠として使うので、この現象そのものを証明しておかなければなりませんが、それについては後で取り上げます。







■　　　　　　zt_dx(s) の構造と零線図


zt_dx(s) は　k(s) を構成する基本的要素であり、根幹とも言える重要関数です。この関数の定義は

zt_dx(s) = Σ_[r=1,dx] 1/r^s

であることは最初に述べています。　1 + 1/2^s + 1/3^s ... と続く綺麗な形をしています。

この関数は　dx が増加しても収束しません。1/dx^s の幅が縮小するので、それに合わせて幅が縮小し、零線図は線ばかりになってゆきます。これでは図にならないので、縦を 10倍するなどして、幅を広げた図を作ります。

右図は　dx=4 のときのものです。まだ幅が広いので、縦はそのままです。k(s) 同様に左から横Ｕ字形が伸びています。k(s) との違いは、k(s) の場合、左へ行くと零線が上に昇るのに対し、zt_dx(s) は横に伸びるだけであることです。















■　　　　　　qnber_dx(s) の細分化


qnber_dx(s) を証明の根拠として使うので、この関数を細分化して、厳密に検討することにします。

qnber_dx(s) はシグマがついているので、総和の形になっています。その個別の式を分析するために、qnber_dx_p(s) を定義します。それを　ｒ　まで合計した式を　qnber_dx_r(s) とします。

つまり、p=4 とすると、qnber_dx_p(s) = B(4)*(s+2)!/4!/(s-1)!/dx^3 　ということで、 r=4 とすると　qnber_dx_r(x) = Σ_[r=0,4] B(r)*(s-2+r)!/r!/(s-1)!/dx^(r-1) 　ということになります。


p=0 と r=0 は同じ式です。B(0)*dx/0!/(s-1)　で、B(0)=1, 0!=1　なので、dx/(s-1) となります。この零線図は　a=1, b=0 にそれぞれ実零線、虚零線が通り、(1,0) で直交しています。それ以外に零線はありません。



p=1 は　B(1)/1! で、B(1)=-1/2、!!=1 なので、-1/2 となります。実部はすべて　-1/2 、虚部は　0　ということなので、実零線はありません。虚部はすべて零ですから、虚零線ばかりというか、線を引くことができません。


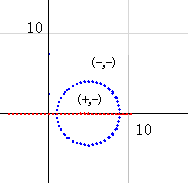r=1 は　p=0 と p=1　を足したもので、どういう図になるか、すぐには思いつきません。しかし、描いてみると実零線の円が登場します。

右図は　dx=4 のときですが、dx が何であれ、円になります。円の大きさは、半径　dx　で、左端が (1,0) 、中心は　(dx+1,0) となります。









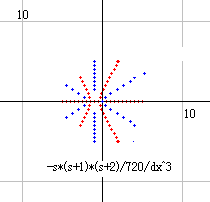
p=2 は　B(2)*s!/2!/(s-1)!/dx^1　で、整理すると s/12/dx　となります。

r=2 は　r=1 に　p2 を加えたものなので、dx/(s-1) - 1/2 + s/12/dx　となります。

dx=4 としたものが右図です。今度は虚零線が輪になっています。この輪は円ではなく、わずかに上下がつぶれています。上記の式に　a=1　を代入し、式を０として、ｂを求めると、輪の上端の値が出てきます。　b=+-dx*√12　ですから、dx が増加すると輪も拡大します。

なお、dx を極大化すると、この輪が円になることは計算上確認できます。





p=3 は　B(3)=0 なので省略します。


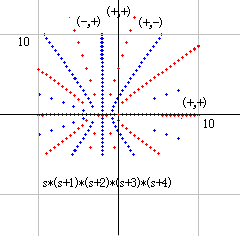
p=4 は　B(4)*s*(s+1)*(s+2)/4!/dx^3　となります。B(4)=-1/30、4!=24　で、整理すると -s*(s+1)*(s+2)/720/dx^3　となります。

右図のように零線が放射状に伸びています。










r=4 は　r=2 に　p4 を加えたもので、右図のようになります。



















p=6 は　B(6)*s!/6!/(s-1)!/dx^5　となります。 放射線の数が増えています。
















r=6 は　r=4 に　p=6 を加えたもので、右図のようになります。dx=6 としてあります。


dx を増やすと零線の幅はますます広くなるので、零線図も広域図になります。dxを増やしたときの図は　qnber_dx(s) の零線図を参照してください。














■　　　　　　qnber_dx_r(s) の　r=2 のときの虚零線の輪


r=2 のときにできる虚零線の輪の形を確定できることが証明の重要な根拠となります。qnber_dx_r(s) で、dx がなんであれ　r=2 の零線図に虚零線の輪ができます。その輪の上端は　(1,dx*√12) と確定します。

証明としては　a=0.5 が重要なので、a=0.5 のときの輪の場所を計算すると　(0.5, √(12dx^2-0.5^2)) となります。dx　は無限大まで拡大する数ですから、この上端と a=0.5 と輪の交点はどこまでも上に伸びてゆきます。

一方、仮定上の零点を持つ零線図は k(s) のものなので、収束した後は変化しません。仮定上の零点はふたつ横に並んで発生するので、同じｂの値を持ちます。dx はどこまでも増加する数ですから、dx*√12がどこかでこのｂを超えることになります。そのときの　qnber_dx_r(s) と　qnber_dx(s) は別の関数ですからｂの値は異なります。しかし、両者は密接な関係にあるので、qnber_dx_2(s) で成り立つことが　qnber_dx(s) でも成り立つ可能性があります。

仮定上の零点がもしあるとするなら、その零線図のｂの値が巨大であることは、計算可能な範囲に仮定上の零点が存在しないことから明らかで、議論の余地はありません。しかし、ｂがいくら巨大であるとしても収束している数ですから、dxが増大するといずれ、それよりも大きな数になることは確実です。qnber_dx_r(s) の　r=2 の虚零線の輪がいずれｂを超えることも確実です。そのときの実部の値がどうなるかを調べてみます。

p=0 のとき、実部の大きさは　dx/(s-1) で決まります。a=1 のとき、実部は０です。a=0.5 のとき、-0.5dx/(0.5^2+b^2)　、a=0 のとき、-dx/(1+b^2) となります。分母がプラスなので、必ずマイナスになります。実零線は a=1 軸上にあるので、この軸の左側はすべてマイナスであることが確実となりました。

p=1 は　実部　-1/2 、虚部　０　です。p=0 と加えると、実部は　a=1 より左側はすべて　-1/2 よりも小さいことになります。（絶対値は大きい。）

p=2 は　実部　a/12dx です。仮定上の零点は　0 < a < 1 の範囲にしかないことはすでに証明されています。ですから、a は 　0 < a < 1 の範囲内で検討すればよいのです。すると、1/12dx より小さくなります。dxはプラスの数なので、1/12 より小さいということです。r=1 の実部は　-1/2　よりも小さいのですから、p=2 を加えてもマイナスのままになります。これで、r=2 のときの　0 < a < 1 における実部値はすべてマイナスであることが明らかとなりました。


次に、p=4, p=6 と加えてゆくとどうなるかを検討します。

p=4 とは　B(4)(s+2)!/4!/(s-1)!/dx^3　で、B(4)=-1/30 です。ｓに関わる部分は　s(s+1)(s+2) なので、s=a+b*i と置き換えると、実部に　-3ab^2-3b^2 が出てきます。これについては　ver20 の「■１の６」、ra(r)関数を参照してください。符号はマイナスですが、B(4) と合わせるとプラスになります。これがｓ部分の最大増加要因です。

b=dx*√12　を　(-3a-3)b^2 に代入すると、(-3a-3)*√12*dx^2 となり、(-3a-3)*√12*dx^2/dx^3 = (-3a-3)*√12/dx となります。a は　0 < a < 1 なので考慮する必要はありません。ゆえに、計算結果は　 dx の増加により零に近づきます。実部最大の増加要因が零に近づくのですから、p=4 の式全体が零に近づきます。すると、総和である r=2 と　p=4 の合計は　b=dx*√12 において必ずマイナスとなります。

p=6 は、B(6)(s+4)!/6!/(s-1)!/dx^5 です。ここも　ｓに関わる部分では、実部式に (5a+10)b^4　が登場します。これがｓ部分の最大値です。これに　b=dx*√12　を代入し、dx^5 で割ると　(5a+10)√12/dx となります。ですから、dx の増加により、ｓ式全体は限りなく零に近づき、それに　B(6)/6! を掛けるのですから、ますます零に近づきます。これを総和である　r=4 に加えると、合計は　r=2 の値とほとんど同じ数になるので、ｂ以下の部分ではマイナスになります。

p=8 も同じで、dx の増加により零に近づくので、総和した結果はマイナスです。

結局　p=4 以降の式はすべて零に近づくので、r=2 との合計は必ずマイナスとなります。つまり、r=2 のときの　b < dx*√12 において、式の値は必ずマイナスになるということです。これは、仮定上の零点がある場所のｂが、dxの増加により、いずれ　dx*√12 より小さくなることは確実ですから、そのときの値が必ずマイナスとなることを意味しています。

ゆえに、仮定上の零点がある場所の　qnber_dx(s) の実部は　0 < a < 1 においてマイナスになることが確定しました。ゆえに、この場所の符号は　(-,-) or (-,+) ということになります。






■　　　　　　qnber_dx(s) の　a=0.5 上の実部値


仮定上の零点がある場所の実部値がマイナスであることは確定しました。しかし、さらに、その値は　qnk_dx(s) の実部から引くために使われるので、値の絶対値（大きさ・範囲）を決めておかなければなりません。絶対値が大きいと、引き算の結果、qnzt_dx(s) の　a=0.5 上の実部零点がなくなり、証明失敗に終わる危険性があるからです。

さて、r=2 のときの　仮定上の零点がある場所（　0 < a < 1　）のｂ値は、(a-1)dx/((a-1)^2+b^2) - 1/2 + a/12dx　です。の絶対値以下となります。p=4 から p=dx までの　qnber_dx_p(s) の実部の値は、最大増加要因が　B(p)/p!/dx なので、b=dx*√12 における実部の値は　p=4 で　-B(4)/4!/dx、p=6 で　B(6)/6!/dx、p=8 で　B(8)/8!/dx　と続き、合計値は、dx の増加によりプラスの極小数になります。一方、r=2 の値は　-1/2 よりわずかに絶対値が小さくなるので、結論として、仮定上の零点のある場所における実部値はマイナスで、必ず絶対値が　1/2 よりも小さくなります。







■　　　　　　ber_dx(s) の零線が横に流れることの証明


仮定上の零点が r=2 の虚零線輪の内側にあるならば、ber_dx(s) の零線はその場所（ 0 < a < 1 ）では、すべて横に流れる形になります。横に流れるとは、直線に近い線ということで、輪になったり、横Ｕ字形にならないということです。上下にある程度動くことはあります。しかし、dx^s の零線が作る上下の壁（これを枠と言うことにします。）を超えることは普通はありません。qnber_dx(s) の零線との交点があるなら、そこを通って別の枠に移動しますが、それも同一方向には一度きりで、２度目の交点があるなら、そこを通って元の枠に戻ります。

つまり、ber_dx(s) の零線は dx^s の枠の中を動くだけで、qnber_dx(s) の交点があってもひと枠移動するだけで、枠を連続して超えて上下に運動することはありません。そのことを「横に流れる」と表現しています。そして、ber_dx(s) の零線が　 0 < a < 1　において、すべて横に流れる形になることを以下のように証明しておきます。


qnber_dx_r(s) の　r=2 の虚零線の輪は　qnber_dx(s) の零線図には現れません。しかし、r=2 の輪内部で、a=0.5 上においては、すべて実部はマイナスであり、実部零点が現れることがないことは先に証明したとおりです。実部零点がないということは、実零線が通っていないということです。実零線がなければ交点はありません。

r=2 の虚零線の内部はすべて虚部マイナスなので零点はありません。しかし、r=4 になると、r=2 の輪はなくなり、その場所を横切る虚零線が１本現れます。この線は最後まで残るので、仮定上の零点がある場所の符号は　(-,-) もしくは　(-,+) というふたつの可能性が残ります。

この　qnber_dx(s) の最後まで残る虚零線は１本だけです。なぜなら、qnber_dx_p(s) の値は　B(p)*(s+2)!/p!/(s-1)!/dx^(p-1) ですから、虚部は　B(p)*rb(p)/p!/dx^(p-1) となります。rb(p) は　s*(s+1)*(s+2)... の展開式で、ver20 （１の６）　で解説してある関数です。rb(p) の増加要因で最大なのが　b^(p-1) で、B(p)*b^(p-1)/p!/dx^(p-1) となります。ｓに関わる式の符号は＋ー変化し、B(p) の符号も＋ー変化するので、掛け合わせると必ずプラスになります。そして、この場合の dx を固定すると、b の増加により、全体の値は必ず増加します。つまり、一度 z=0 を超えると、その後、０に戻ることはありません。ですから、虚零線は１本しかありません。

その一本の虚零線が上下左右に湾曲する可能性は残っています。もし、湾曲せずに 1/dx^s との交点が発生しない場合、ber_dx(s) の零線が枠を超えることはないので、「横に流れる」と表現できます。もし、交点があるなら、以下のようになります。

式の形は割り算ですが、割り算の符号計算のやり方はまだ説明してないので、便宜上、「 1/dx^s を掛ける」と考えます。dx^s と　1/dx^s は同じ零線図になります。ただし、符号が異なります。虚零線の上枠が　(+,-) or (-,+) となります。qnber_dx(s) の符号が　(-,-) の場所では　(+,-)*(-,-) = (-,?)　or　(-,+)*(-,-) = (+,?) なので　ｒ区域になります。この区域の下側にある虚零線同士の交点は新しい虚零線の通過点になるので、新しい虚零線はそこを通って右下の区域に移動します。ひとつ上の区域は　ｂ区域なので、そこを通る新しい実零線は下を走る実零線と虚零線の交点を通って、右下の区域に移動します。つまり、斜め下に下る形で横に流れます。

「斜め下に下る」と言っても、ひと枠だけです。そのひと枠の幅は　pi/ln(dx) で決まります。ですから、大きく下るわけではありません。ですから、全体として、大きな揺れはなく、「横に流れる」ことになります。

qnber_dx(s) の零線（桃線）が大きく振動して、山や谷が出来る場合も、ber_dx(s) の零線の形を崩すほどの影響は与えません。その理由は、qnber_dx(s)の零線が元のdx枠に戻るとき、ber_dx(s)の零線もまた元に戻すことになるからです。ber_dx(s)の零線は dx ふた枠に渡って移動することはありません。ですから、この形も「横に流れる」と表現することは可能となります。

qnber_dx(s) の桃線が左右に振動する場合も同じです。ber_dx(s) の零線は交点を通ってひとつ別枠に移動するだけなので、「横に流れる」形を崩すことはありません。

以上のことを踏まえて　zt_dx(s) の分析をすることになります。













■　　　　　　仮定上の零点がある場合の矛盾点


そこで、仮定上の零点を持つ零線図を分析します。これについては、すでに　 ver20 でどのような図になるかは説明済みで、まだ証明できてない零線図は数種類あります。ここではその中のひとつを取り上げます。もし、この証明が成功しているなら、他の零線図についても同じやり方で証明してみようと計画しています。


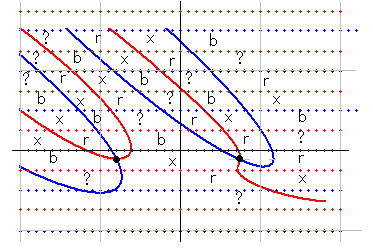
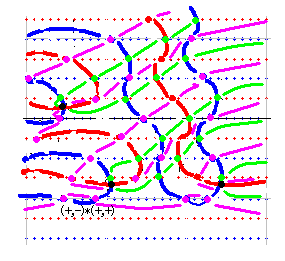
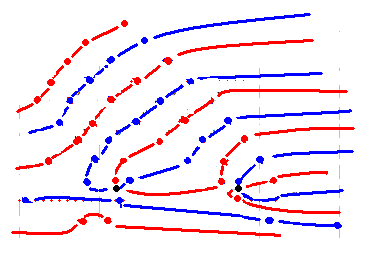
取り上げる零線図は ver20 で想定した形のひとつで、右図のようなものです。この図を使って、仮定上の零点を持つ場合の　zt_dx(s) 図と、qnzt_dx(s) の図を求めます。これは、ひとつめ、ふたつめ、３つめ、４つめという４通りの図になりました。

次に　逆周りの作業で qnzt_dx(s) を求めます。右図から　qnk_dx(s) を求めます。次に　qnk_dx(s) - qnber_dx(s) というやり方で　qnzt_dx(s) を求めます。先の qnzt_dx(s) と　後の　qnzt_dx(s) は同じでなければなりません。

この作業の結果、「４つとも矛盾がある」と言えれば証明は成功となります。しかし、残念ながら矛盾は見つかりませんでした。このままでは証明失敗ということになります。しかし、ひとつめ、ふたつめ、４つめには　a=0.5上の実部零点に矛盾が生じることが発見できました。また、３つめについては、zt_dx(s) との関係で矛盾が発生することが証明できました。結果として４つとも矛盾があると言えるので、証明は完成したと言えると思います。

その作業の詳細は以下の通りです。




■　　　　　　zt_dx(s)、qnzt_dx(s)を求める


まず最初に、仮定上の零点がある場合の zt_dx(s) の図を求めます。計算式は　zt_dx(s) = k_dx(s) - ber_dx(s) です。実際の計算はできないので、符合計算の引き算を使います。

ber_dx(s) の零線は　1/dx^s （dx^s）とほとんど同じように横に流れます。それについては先に述べたとおりです。1/dx^s は横直線ですが、ber_dx(s) はだいたいまっすぐという程度で、やや斜めか、少し上下に動きます。証明としては大きく曲がる場合も踏まえなければなりません。ただし、「大きく」とは言うものの、先に述べたように、1/dx^s 　のひと枠の幅か、せいぜいふた枠ですから、たいして大きくはありません。また、k_dx(s) の図そのものが歪んだものなので、ber_dx(s) の曲がり方を詳細に検討する意味はありません。検討すべきは　0 < a < 1 の範囲だけですから、1/dx^s (dx^s) の線よりやや上か下を ber_dx(s) の零線が横に走ると考えれば充分です。さらに考えると、交点さえ発生させれば良いので、1/dx^s の線と同じものであっても差し支えないことになります。

そこで、先の 1/dx^s の図を流用することにします。図は直線になっていますが、線を歪ませても結果は同じであることはお判りいただけると思います。その図を使って　k_dx(s) - ber_dx(s) という符号引き算を実行します。


先の横Ｕ字形がふたつ登場する図を使います。横線も同じですが、ber_dx(s) に変更されているので、やや歪みがあることは許容されます。

k_dx(s) 横Ｕ字形内部の虚零線下側が　(-,-) です。ber_dx(s) 青横線の上側は(+,+) か (-,-) になります。まずは　(+,+) として計算します。(-,-)-(+,+) = (-,-)　となり、その区域は　ｘ区域となります。その上の区域は　(-,-) - (+,-) = (-,?) となり、ｒ区域となります。

同じ色の零線の交点はその色の零線が通ります。異なる色の交点はどちらも通りません。この原則に則って線を引きます。



青横線の上側が　(-,-) の場合もあります。その場合は右図の区域判定になります。















この２種類の零線図のそれぞれについて、符号計算の規則に従って引き算を実行します。線の引き方は一通りでなく、４つの可能性が生まれます。どちらの零線図でも同じ結果になるので、結局、４通りの　zt_dx(s) 図を得ることができます。

ひとつめは、左の小さい青横Ｕ字形がない場合と、ふたつめは、左の小さい青横Ｕ字形がひとつある場合、３つめは、ふたつ並ぶ場合、４つめは、入れ子になる場合です。

小さい青横Ｕ字形が３つ並ぶ場合、４つ以上並ぶ場合、小さい青横Ｕ字形が入れ子になる場合は３つめに含めます。







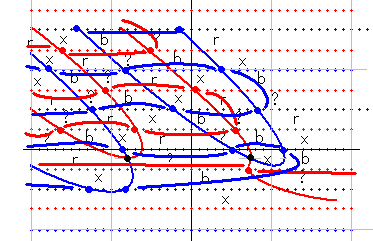ひとつめは、左から真横に横Ｕ字形が伸びてくる形です。
















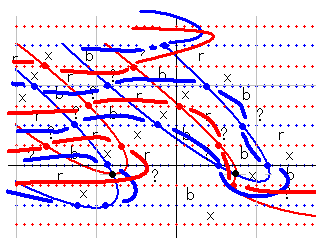ふたつめは、左上から横Ｕ字形が下りてくる形です。小さい横Ｕ字形がひとつあります。













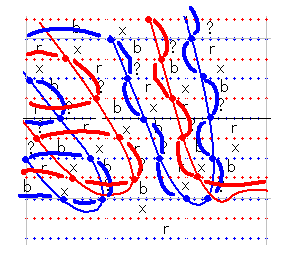３つめは、左の小さい青横Ｕ字形がふたつある場合です。















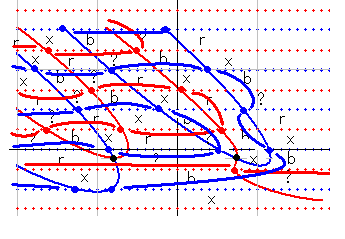４つめは、青横Ｕ字形が入れ子になる形です。

















■　　　　　　ひとつめの形


ひとつめは、左横から伸びる形になる零線図です。古い零線を消すと右図のようになります。これが 仮定上の零点がある場合の　zt_dx(s) の零線図です。













これに　dx^s を掛けると右図のようになります。これが　qnzt_dx(s) の図です。

dx^s の零線は前の図の横線を代用していますが、新しく線を引いても同じ結果になるので、大目に見てください。

区域判定では青・赤線だけで考えるので、緑線、桃線のない状態で判断されます。真ん中の青横Ｕ字形内部の赤線下側が zt_dx(s) では　(-,-) で、そこを通る dx^sの赤点線の下側が　(+,-)　か　(-,+) です。この区域は　(-,-)*(+,-) = (-,?) もしくは、(-,-)*(-,+) = (+,?)　で、どちらも ｒ区域と判定されます。すると、赤線の右側がｂ区域、上にある赤点線の狭い区域がｂ区域、その上の赤線の上がｒ区域となります。以下同様なので、計算なしに区域判定ができます。

新しい零線（qnzt_dx(s)の零線）は、実零線が緑、虚零線が桃で示してあります。実零線は、右無限では　dx^s と同じ場所から出発し、左に向かって横Ｕ字形を作ります。虚零線は、右無限では dx^s と同じ場所から出発しますが、横Ｕ字形になるのと、左に抜けてゆくものとがあります。



これから古い線を消したものが右図です。
















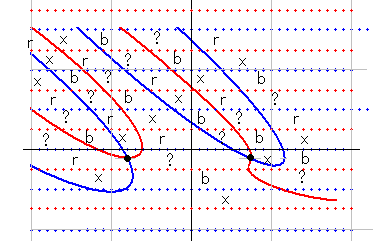
■　　　　　　ふたつめの形


ふたつ目は、左上から青横Ｕ字形が下りてくる形です。

















これに　dx^s を掛けると　qnzt_dx(s) になります。dx^s は　1/dx^s と同じ線ですが、符号は異なります。点線で示してあるのが dx^s の零線です。赤横点線の上側が　(+,+) or (-,-) となります。掛け算なので、ｂ、ｒ　区域しかありません。同種の零線の交点は桃点、異種の交点は緑点となります。古い線との区別のために、新しい実零線は緑線、虚零線は桃線にしてあります。












古い零線を消すと右図になります。
















■　　　　　　３つめの形


３つめは、左の小さい青横Ｕ字形がふたつある形です。これが仮定上の零点があるときの　zt_dx(s)　の形です。















これに　dx^s を掛けます。

横点線が　dx^s の零線です。青横点線の右端から新しい実零線（緑線）が伸びてきます。赤横点線の右端から新しい虚零線（桃線）が伸びてきます。それぞれの区域と交点を通り、青・赤線の交点（黒点）を通ります。新しい零線は、交点以外では古い零線を超えることは出来ません。また、新しい零線同士の交差は一度きりです。この原則で線を引くと右図になります。

黒点に近い場所では、線の引き方について、しばしば別の可能性が生じます。その図も検討対象として残ります。






古い線を消すと右図になります。
















■　　　　　　４つめの形


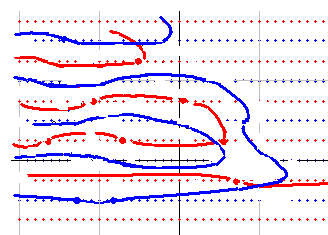４つ目は、青線が入れ子状態になる形です。















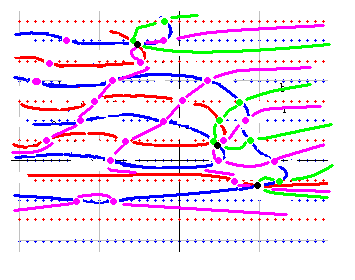zt_dx(s) に　dx^s を掛けると　右図のようになります。
















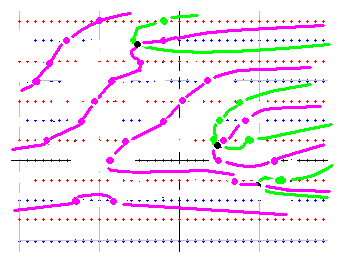古い線を消すと右図になります。

黒点近くでは、別の線の引き方があることがわかりますが、それも検討対象です。




以上で４種類の　qnzt_dx(s) 零線図が出来上がりました。これが逆回りの手順で作図したとき、同じ図になるはずです。その際、矛盾が生じているかどうかを確認します。









■　　　　　　逆回り手順での　qnzt_dx(s) 作図


逆回りとは　k_dx(s) に　dx^s を掛けて qnk_dx(s) を求め、その次に　qnk_dx(s) から　qnber_dx(s) を引いて qnzt_dx(s) を求めるやり方です。

仮定上の零点は計算可能な範囲には存在しません。存在するなら、その場所まで収束が進むために　 dx がかなりの巨大数にならなければなりません。収束すれば、k(s) と k_dx(s)　は同じ零線図になります。しかし、dx^s は、零線の幅が　pi/2/ln(dx) で決まるので、ほとんど作図できないほど狭くなります。そこで、以下の作図においては、便宜上、dx を適当な数にして、見た目の幅がある程度あるようにして描いてあります。ご了解ください。

仮定上の零点を持つ零線図は　k_dx(s) のどこかにあると想定します。その場所の　qnk_dx(s) の図は、k_dx(s) と　dx^s を重ねて掛け合わせた図になります。これは符号掛け算で計算します。dx^s の零線図は、実零線も虚零線も真横に流れる直線なので、描くのは簡単です。また、幅も一定です。問題は上下のずれがあることですが、しばらく上にずらすと、ひとつ上の零線と重なるので、分析の幅はあまり広くありません。また、dx が大きいと、その幅は狭くなるので、検討すべき図は多くはありません。

まずは適当に線を引いて検討します。

dx^s は、虚零線（赤線）の上が　(+,+) か (-,-) です。その理由は　dx^s = dx^a * (cos(b*ln(dx)) + i* sin(b*ln(x))　なので、b=0 より上が　(+,+) になるからです。

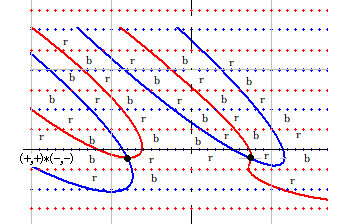
k(s)　の零線図の符号は決まっています。青横Ｕ字形内の赤線の下側が (-,-) となります。その区域で掛け算を実行します。つまり、　(+,+) * (-,-) = (?,-) です。これは実零線が通る区域ということで　b　の印をつけます。その隣は虚零線の通り道なので　ｒ　の印をつけます。零線図全体にこの印をつけたのが右図です。

なお、虚零線（赤点線）の上が　(-,-) でも計算結果は同じになります。(-,-)*(-,-) = (?,+)　となるからです。






赤線と赤点線の交点、青線と青点線の交点を新しい虚零線（太い赤線）が通ります。この点に赤点を付けます。赤線と青点線、青線と赤点線の交点は新しい実零線（太い青線）が通ります。この点に青点を付けます。あとは通過可能な区域を通り、すべての交点を通過する形になるように線を引きます。新しい実零線、虚零線は太線で引いてあります。その結果のひとつが右図です。

左右の黒点を通る零線がどの線と繋がるかにより形が変わります。それを数えると４種類になります。また、dx^s の実零線と虚零線を取り換えた図も４種類に分かれます。合計８種類の図が出来上がります。この８通りの図をすべて分析するべきなのですが、結果を先に述べておくと、この分析結果は、矛盾がある場合とない場合に分かれます。ということは全体として「矛盾がない」という結論なので、あまり詳しく解説しても意味がありません。そのうちのひとつだけを取り上げることにして、あとは省略します。





古い線は必要ないので消しておきます。

これが仮定上の零点がある場合の　qnk_dx(s) の図です。

これから　qnber_dx(s) を引くと　qnzt_dx(s) 零線図が出来上がります。










■　　　　　　逆からたどるひとつめの形



さて、仮定上の零点がある場所の　qnber_dx(s) の符号は　(-,+) or　(-,-) に限定されることは先に証明したとおりです。


qnk_dx(s) の符号については、特に法則が見つかっていません。青横Ｕ字形の外側に注目すると、そこはあらゆる符号を取る可能性があるので、すべてを検討することになります。

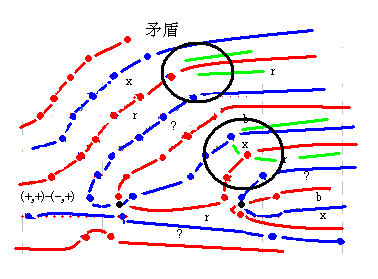
まずは、qnk_dx(s) 零線図の中央にある青横Ｕ字形の左外部分を　(+,+) としてみます。そこは　qnber_dx(s) の　(-,+)　部分とすると、符号引き算で　(+,+) - (-,+) = （+,?) となるので、その場所は　qnzt_dx(s) の　ｒ区域になります。あとはそれを基準に判定します。

右図の場合は、緑線が ｘ区域を通ることになるので、この場合は、「矛盾あり」と判定されます。





しかし、qnk_dx(s) 横Ｕ字形左側を　(-,+) とすると、(-,+) - (-,+) = (?,?) で　？区域と判定されます。これは、「矛盾なし」と判定されます。

この緑・桃線は「ひとつめの形」と同じですから、形の面からして矛盾はありません。









中央の青横Ｕ字形左外側が　(-,-) の場合は、(-,-) - (-,+) = (?,-) で　ｂ区域と判定されます。この図に緑・桃線を引くことに問題はありません。ゆえに、この図は「矛盾なし」と判定されます。

また、(+,-) の場合は、(+,-) - (-,+) = (+,-)　で　ｘ区域と判定されます。この図は零線を引けないので、「矛盾あり」と判定されます。





qnber_dx(s) が　(-,-) の場合も同じように分析しますが、結果は同じで、「矛盾なし」と「矛盾あり」の両方が発生します。全体としては、ひとつでも「矛盾なし」と言う事例があるなら、全体が「矛盾なし」ということになるので、「ひとつめの形の　qnzt_dx(s) には矛盾がない」という結論になります。

そこで、このやり方は諦めて、別の矛盾を探すことにします。








■　　　　　　a=0.5 上の角度変化矛盾



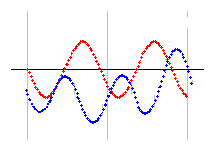別の矛盾とは、　a=0.5 上の角度変化についての矛盾です。これは　qnk_dx(s) から　qnber_dx(s) を引くという零線図の符号計算ではなく、a=0.5 上の角度計算を使って分析します。つまり、qnzt_dx(s) のひとつめの零線図の a=0.5 上に実部・虚部零点とが交互に現れないところに注目します。

右図は、qnzt_dx(s) のひとつめの零線図上の a=0.5 ｙｚ図を想定したものです。このようになっていると矛盾と判定できます。なぜかということを以下に説明します。





qnzt_dx(s) のひとつめの図を再掲しておきます。

この図の中央を縦に走る線が　a=0.5 軸です。この軸の左右等距離のところに仮定上のリーマン零点があるとして作図した qnk_dx(s) の図を使って、符号計算の結果出来上がったものです。真ん中と下にある実零線（緑線）横Ｕ字形は　a=0.5軸を通ることはありません。ですから、その部分には　a=0.5 軸上の実部零点はありません。

もし、実零線（緑線）の一部が伸びて、a=0.5 軸と交わるとするなら、実部零点がふたつ並ぶことになります。これも問題です。

a=0.5 軸は　k(s) にとって重要な軸であり、角度公式もあるほど変化のはっきりしている場所です。これに dx^s を掛けると　qnk_dx(s) になりますが、dx^s も角度変化のはっきりしている関数です。ですから、qnk_dx(s) の角度は公式化することができます。これから　qnber_dx(s) を引くと　qnzt_dx(s) になりますが、角度変化に焦点を当てて分析すると、qnzt_dx(s) の角度にも何らかの法則があるのではないかと思われます。

そこで、qnk_dx(s)、　qnber_dx(s) と　qnzt_dx(s) の a=0.5 上の角度変化を調べてみます。






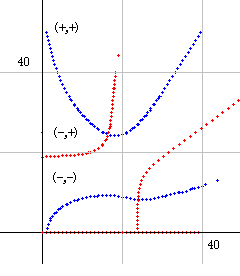
■　　　　　　qnk_dx(s) の　a=0.5 上の角度変化とｙｚ図


qnk_dx(s) の角度公式は、このＨＰの最初のところですでに説明してあります。再掲すると次の式になります。

qnk_dx_θ(s) = b*ln(dx) - 1/2 * { b*ln(b) - b*ln(2*pi*e) - pi/4 + ... }

なだらかに変化するので、実部波・虚部波とも普通の波の形をしていて、z=0 と必ず交互に交わります。仮定上の零点がある場所でも　a=0.5 上の変化はありません。


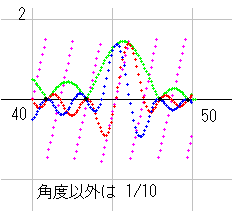右図は　qnk_dx(s)　の　a=0.5, dx=16, で、ｂが40 から 50 までを計算により求めた図です。青が実部波、赤が虚部波、緑が絶対値、桃が角度を示しています。波の高さが高いので、角度以外はすべて　1/10　にしてあります。

qnk_dx(s) は dxがある程度大きいと、k(s) と同じ場所にリーマン零点を持ちます。青線が z=0 に近いところで山を作っている場所にリーマン零点があります。角度は零点の影響を受けません。仮定上の零点がある場所も同じで、a=0.5 上の角度に影響はありません。しかし、零線図には仮定上の零点が現れます。その零点が現れた図がかなり前に掲げた qnk_dx(s) の零線図になるわけです。a=0.5 軸から等距離のところにある黒点がリーマン零点です。そして、a=0.5 軸上を実零線と虚零線が交互に通過していることが確認できます。

qnk_dx(s) は　dx の幅に合わせて波が発生するので、波の幅は狭くなります。しかし、k_dx(s) は dx が大きいところでは収束するので、幅は k(s) と同じになり、波の幅は広いままです。qnk_dx(s) の波の数は増え、幅は狭くなりますが、リーマン零点の場所は変化しません。ゆえに、零点のない場所にも波が発生します。この　qnk_dx(s) は実際に存在する図ですが、仮定上の零点がある場所でも同じことが起こります。



仮定上の零点を持つ　qnk_dx(s) ｙｚ図から qnber_dx(s) のｙｚ図を引きます。その　qnk_dx(s) 図は、先の dx=16 図　から推測できます。dx　が大きいと、リーマン零点とリーマン零点の間に無数の普通波が存在することになります。しかし、それでは図示できないので、便宜上、右隣が近いとして描きます。そして、仮定上の零点がある場所は、qnk_dx(s) では普通波になるので、ｙｚ図での変化はありません。ですから、そのまま左隣のリーマン零点の波になります。


それは右図のようになります。

桃線の角度は右肩上がりでほぼ直線です。ですから、リーマン零点でない場所では、実部波と虚部波が交互に z=0 線と交わります。









これが qnk_dx(s) の図です。これから　qnber_dx(s) を引くと　qnzt_dx(s) になります。引き算の場合の角度は単純には扱えません。そこで、ｚ値で引き算することにします。

qnk_dx(s) = k_dx(s) * dx^s です。dx^s = dx^a * {(cos(b*ln(dx))+i*sin(b*ln(dx))} なので、dx^a のみが増加要因となります。a=0.5 で、大きい数とは言えませんが、dx はどこまでも増加するので、dx^a もどこまでも増加する数になります。k_dx(s) の実部が小さい数であっても、その値は収束後なので定数となります。それに対して、dx は増加する数なので、qnk_dx(s) のa=0.5 実部はどこまでも大きくなります。

qnk_dx(s) の a=0.5 上角度はなだらかな増加なので、実部・虚部ともに波になります。dx^a の増大にともない、波はより大きくうねります。実部が大きくなるということは虚部も大きくなるということで、仮定上の零点がある場所でもうねりは大きくなります。そのときの最大実部値は　1 より大きく、うねりの下側は　-1 より小さくなります。

この　qnk_dx(s) の実部から　qnber_dx(s) a=0.5 の実部を引くと qnzt_dx(s) の実部になります。qnber_dx(s) の実部は　a=1 のときマイナスで、絶対値は　1/2 より小さいことは証明されています。a=0.5 もマイナスで、絶対値 1/2 に近い値を持ちます。qnk_dx(s) の実部波のマイナス部分は　-1 より小さいので、-1/2 に近い数を引くとは、1/2 に近い数を足すことで、答えは必ずマイナスになります。そして、qnk_dx(s) は波の形をしていて、qnber_dx(s) は横線ですから、qnzt_dx(s) の実部は必ず波になり、プラスからマイナスに移動する途中で必ず z=0 と交わることになります。この交点が実部零点です。

a=0.5 上に実部零点があるということは、qnzt_dx(s) 零線図の a=0.5 上を通過する実零線がなければなりません。ところが、ひとつめの零線図には　a=0.5 軸と実零線の交点が発生していません。ですから、これは矛盾であると判定できます。








■　　　　　　逆からたどるふたつめの形


ふたつめの形については、ひとつめと同じ論理が適用できます。

仮定上の零点がある場所の　qnber_dx(s) の符号は　(-,+) or　(-,-) だけであり、これを前提にした零線図分析では、矛盾は指摘できません。しかし、a=0.5 軸を実零線が通過しない場所があるので、矛盾と判定されます。


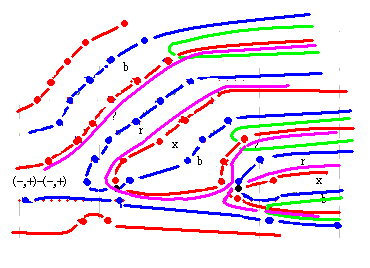
右図が　qnzt_dx(s) のふたつめの形です。

真ん中の黒縦線が a=0.5 線です。この線上を緑線、桃線が交互に通過しなければなりません。しかし、一番上の緑横Ｕ字形の緑線は　a=0.5 を通過することはありません。ゆえに矛盾となります。

また、もし、緑線の一部が a=0.5 を超えて左側に進出するなら、それが戻るときに、もうひとつの実部零点を作ります。この２番目の実部零点は　qnzt_dx(s) のｙｚ図にないものなので、これも矛盾となります。








■　　　　　　逆からたどる３つめの形


zt_dx(s) から作った　qnzt_dx(s) の３つめの零線図を再掲しておきます。

最初に、qnzt_dx(s) = qnk_dx(s) - qnber_dx(s) というやり方で求める零線図が右図と一致するかどうかを分析します。まず、qnk_dx(s) に　qnber_dx(s) の零線図を重ねて符号計算（引き算）を実行します。qnber_dx(s) は零線の数が少なく、交点があまりないので、もっぱら区域計算のやり方で新しい零線図を求めます。










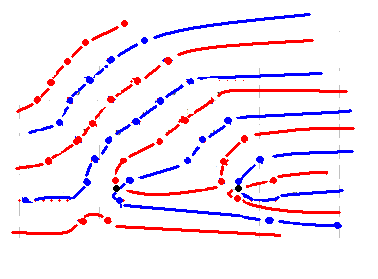qnk_dx(s) の図にはいくつかありますが、矛盾が生じない図がひとつでもあると、全体が矛盾なしとなります。分析の結果、矛盾のない零線図が見つかりました。ですから、矛盾の生じる事例を説明しても意味はないので、矛盾の生じない図を取り上げます。それが右図です。これは、先の図と異なり、左リーマン零点を通る実零線の繋がる相手が変化し、入れ子状態になっています。この図にqnber_dx(s) を重ねて、引き算を実行します。

qnk_dx(s) の一番下側の虚零線の上を　(+,-) とします。そして、この区域全体が　qnber_dx(s)で　(-,-) のときを検討します。すると、次の図になります。



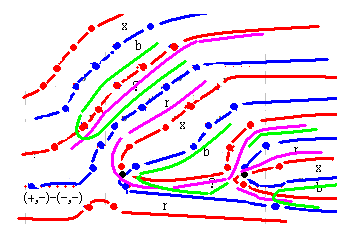入れ子の実零線外側が (+,-) なので、(+,-)-(-,-) を実行すると　(+,?) になります。ここは　ｒ区域です。あとは法則通りに判定し、なるべく　qnzt_dx(s) の図に近いところに線を引きます。すると、やや苦しい形であるにしても、線を引くことはできます。つまり、矛盾は生じないということです。

ひとつの事例でも矛盾がなければ、全体が矛盾なしと判定されます。ですから、その他の図を検討する必要はありません。３つめの形には矛盾がないという結論になります。


また、qnzt_dx(s) の　a=0.5 上に、緑線、桃線が交互に現れているので、ここにも矛盾はありません。

証明を完成させるためには、別の矛盾を探さなければなりません。そこで、方針を転換して、３つめの形については、zt_dx(s) の形そのものがありえないことを証明することにします。






■　　　　　　zt_dx(s) の３番目の形はありえないことの証明


k_dx(s) から　ber_dx(s) を符号引き算したときに出来る零線図は４つありますが、今回取り上げているのは、この３番目の図ということです。１番目と２番目の零線図については、すでに矛盾が生じることが証明されています。残った３番目にはどういう矛盾が生じるかがここでの課題となっています。

この３番目は、上から垂れ下がっている横Ｕ字形の左側に、小さな横Ｕ字形がふたつ並んでいる形です。その小さな横Ｕ字形がもうひとつ増えても、さらに増えても、構造は同じなので、この３番目に含まれると考えてください。

この小さい横Ｕ字形がどこまで並ぶかと言うと、k(s) の下に垂れ下がる横Ｕ字形の出発点まで続きます。dx が増えると、小さい横Ｕ字形の数は非常に増えることになります。もっとも、途中で止まることも許されます。k_dx(s) から　ber_dx(s) を引くと、zt_dx(s) の横Ｕ字形がどこから出発しても差し支えありません。また、小さな横Ｕ字形どうしが入れ子になることも可能です。ですから、零線図の形はいろいろあるのですが、皆同じ構造のをしているので、その代表として３番目を取り上げるということです。


zt_dx(s) の３番目の図を再掲しておきます。

この図は、仮定上の零点を持つ k_dx(s)の零線図から、ber_dx(s)　の零線図を符号引き算により求めたものです。zt_dx(s) は　dx の増加とともに、いろいろな形をとります。ときには入れ子形にもなります。しかし、横Ｕ字形が上から垂れ下がるという形は計算上は見つかりません。そこで、この形がありえないことを符号計算を使って証明してみようと思ったのですが、これはうまくいきませんでした。

今回は別のアイデアで証明を完成させました。それは、dx の増加により横Ｕ字形の幅が減少し、零線の数が増え続けるという現象を使うやりかたです。この現象を零線図全体で見ると、横Ｕ字形が積み重なってゆくように見えます。横Ｕ字形の数は無限なので、数が増えるのではありません。dxが増えると、前あった場所より下に移動するということです。

次の図をみるとよくわかります。


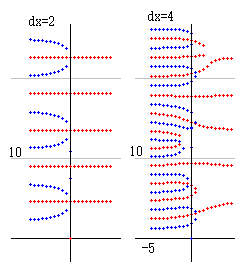
左が　dx=2 のときの　zt_dx(s) 図で、右が　dx=4 のときのものです。

dx=4 のほうが横Ｕ字形の数が多いことがわかります。dx=8　とするとさらに数が増えます。なぜ増えるかと言うと、zt_dx(s) の式を見ると理由がわかります。

zt_dx(s) = Σ_[r=1,dx] 1/r^s　なので、1 + 1/2^s + 1/3^s + ... + 1/dx^s 　となり、最後の項目に　1/dx^s が必ず登場します。dx が増えるとは、1/dx^s を加えるということです。1/dx^s だけを考えると、すべて横直線の零線図になります。これはすでに前のどこかに載せてありますが、dx が増えると、零線の間隔が狭くなることを意味しています。この間隔が狭くなった零線図を加えるとは、符号足し算を実行することです。交点が新しい零線の走る場所に変更になります。そして、交点は零線の幅が狭くなっているので、交点同士の幅も狭くなり、そのため、新しい零線図において零線の幅が狭くなるという結果になります。1/dx^s の幅は零線図全体で同じですから、変化は零線図のどこでも同じように発生し、ｂの大小に関係しません。ですから、全体が縮むように見えるのです。

さて、この現象は仮定上の零点がある場所でも起こります。dx がある程度大きくなると k_dx(s) の零線図は確定します。zt_dx(s) は確定しないので、見た目の違いはますます大きくなります。そして、k_dx(s) が確定したときの　zt_dx(s) の図が先に掲げた　「３番目の図」です。dxを増やしても k_dx(s) は変化しません。しかし、zt_dx(s) は変化します。どのように変化するかは　1/(dx+1)^s を加えると判ります。



そこで、先の仮定上の零点がある場合の zt_dx(s) 図に　1/(dx+1)^s 図を符号足し算で加えてみることにします。これによって出来た零線図とber_dx(s) を加えても、前と同じ k_dx(s) の零線図にならなければなりません。なぜなら、k_dx(s) はすでに収束していて、変化しないからです。

1/dx^s の零線図と 1/(dx+1)^s の零線図は　dx が大きいと見た目にはまったく同じ図になってしまいます。それでは説明ができないので、便宜上、dx が小さいところの零線図を使って説明します。dx が大きくても論理は同じですから、証明としては有効になります。

最初の　zt_dx(s) 図では、横に流れる零線の左端とzt_dx(s) の零線が同じ場所になっています。これは左無限大で一致することを踏まえて、作図上近くに描いただけで、実際の図では近くない場合もあります。しかし、左に進めばいずれ近づいてくることは確定しています。ですから、作図の根拠として使えます。1/(dx+1)^s の零線は別の場所を走るので、zt_dx(s) と横直線の一致はなくなります。しかし、新しい　zt_dx(s) つまり、zt_(dx+1)(s) の零線とは一致します。

zt_dx(s) の符号は k(s) と同じで、青横Ｕ字形内部の赤線の下側が (-,-) となります。1/dx^s は　b=0 の上側が (+,-) なので、赤直線の上側が　(+,-) or (-,+) となります。仮定上の零点がある場合の　dx は大きいので、dx^s の零線図との重なり方はあらゆる可能性を取ります。しかし、zt_dx(s) の零線と　zt_(dx+1)(s) の零線の幅の変化はごく僅かなので、1/(dx+1) の２本の零線の間に入る zt_dx(s) の零線は２本だけです。どこかで３本となるところもありますが、それは (pi/2/ln(dx) - (pi/2/ln(dx+1) の答えに　dx を掛けたものが　pi/2/ln(dx) を超えるところとなります。


ひとまず、「２本を挟む」という条件で符号足し算による零線図を描いてみます。zt_dx(s) の横Ｕ字形内部の虚零線下側が (-,-) であることは　k(s) と同じです。1/dx^s の虚零線の上側が　(-,+) or (+,-) であることはすでに指摘してあります。

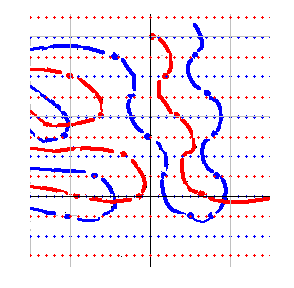右図は　zt_dx(s) に　1/(dx+1)^s を重ねた図です。dx^s と重ねた図とほとんど同じに見えるかもしれませんが、青横線、赤横線の場所が異なっています。また、zt_dx(s)の零線が1/(dx+1)^s の左の同じ色の無限点に繋がりません。













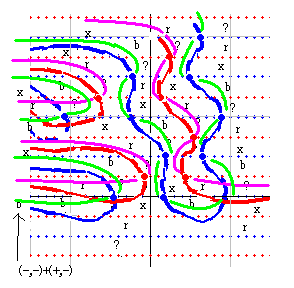赤横線の上側を　(+,-) として符号足し算を実行した結果が右図です。

緑・桃線が新しい実零線、虚零線です。

この新しい図では、横Ｕ字形が前の zt_dx(s) の横Ｕ字形の上側に来ています。これは、dxが増加しているにも関わらず横Ｕ字形が下に移動しないという矛盾があります。

矛盾があるということは、このような図になることはないことを意味しています。








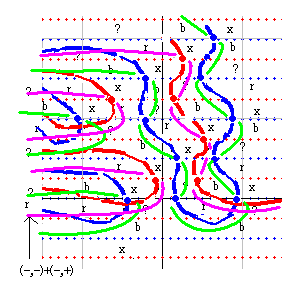赤横線の上側を　(-,+) として符号足し算を実行した結果が右図です。

新しい横Ｕ字形（緑線）が古い横Ｕ字形（青線）よりも下に描かれているので、矛盾はありません。



しかし、dxはいくらでも増える数なので、その次に　1/(dx+2)^s を足すと、横Ｕ字形がさらに下に下がることになります。1/(dx+3)^s を足すと、それよりさらに下がります。もし、下がらなければ矛盾となるので、結局は必ず下がることになります。これは何度も繰り返されるので、結局、一番下の横Ｕ字形は、さらに下の横Ｕ字形の場所まで移動し、形も普通の横Ｕ字形に変わることになります。そして、２番目の小さいな横Ｕ字形が１番目横Ｕ字形になり、３番目にある下に垂れ下がる横Ｕ字形が２番目の場所に移動します。しかし、これで終わりではありません。さらに dx は増えるので、２番目の小さな横Ｕ字形も下に移動し、垂れ下がる形の横Ｕ字形が１番目の横Ｕ字形の場所まで移動することになります。このとき、小さな横Ｕ字形はもうありませんから、先に分析した１番目の零線図と同じ形になります。

この１番目の形はすでに矛盾が生じることが証明されています。矛盾となる形を生じさせるということは、その前の形に矛盾があるということです。ゆえに、この形の　1/(dx+1) の図の足し算には矛盾があることになります。






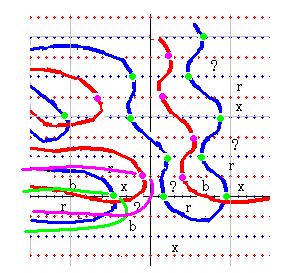zt_dx(s) の零線の間に３本の零線が入る場合もないわけではありません。図の中のどこか一か所が３本を間に含む形になります。どこが３本かで、形が異なりますが、まずは一番下の横Ｕ字形が３本を含む時を検討します。

一番下にある青横Ｕ字形の内部に赤点線が二本、青点線が一本挟まれていることが確認できます。この形で符号足し算を実行すると、前の分析と同じ結果となります。つまり、横Ｕ字形が下にずれてゆくという変化になります。するとやがて一番目の零線図と同じ形になります。

３本を挟む形がどこに現れても、下か上にずれることになり、上にずれることは矛盾ですから、結局下にずれることになり、ひとつめと同じ形に行き着きます。するとそれは矛盾と判定されます。ゆえに、３番目の零線図はありえないということになります。

３番目の零線図がないので、qnzt_dx(s) の３つめの形もないことになります。







■　　　　　　逆からたどる４つめの形


３つめまでの証明が終わりました。４つめの qnzt_dx(s)零線図を再掲しておきます。

zt_dx(s) 図は実零線が入れ子になっていますが、qnzt_dx(s) では虚零線が入れ子になっています。これは、入れ子にならないように作図することも可能です。また、別の作図も可能です。しかし、結論を先に述べておくと、qnk_dx(s) からたどると零線図における矛盾は指摘できません。それはひとつめの形と同じです。

そこで、a=0.5　軸と実零線の交点と虚零線の交点が交互に現れないことに着目することにします。この図の下半分にあるふたつの緑横Ｕ字形は　a=0.5軸と交わっていません。ゆえに実部交点はありません。ｙｚ図で言うと、実部零点（ z=0 ）がないということです。しかし、仮定上の零点を持つ場所では、dx が巨大であるなら、qnk_dx(s)の実部線は大きな波になっていて、qnber_dx(s) の実部は　-1/2 あたりを横に進む線なので、合計した結果のｙｚ図は、巨大実部波が少し上にずれただけで、z=0 との交点は必ず発生し、消えることはありません。しかし、右の図では a=0.5 との交点が消えているので、これは矛盾と判定できます。これはひとつめの証明と同じ論理となります。






これで全部の形を検討したことになります。そのすべてにおいて矛盾を指摘できたので、証明は完成したことになります。

ただし、ここでおこなわれた証明は、仮定上の零点を持つ零線図のひとつについてだけですから、もし、上記の証明の論理が正しければ、それを用いて、残りのk(s)零線図についても分析することになります。おそらく、同じ論理で証明できると思います。

今までは、このひとつの形についてでさえ証明がうまくいきませんでした。もし、間違いがあるとするなら、この中にあるはずですから、しばらくここまでの証明を精査してみるつもりです。








ーーーーーーーーーーーー　　　証明終わり　　　ーーーーー









表紙に戻る



ご感想、ご質問、ご意見などは、Mailのアドレス（hirokuro303@gmail.com）へお願いします。