リーマン仮説（リーマン予想）の証明　ver5.0

「証明できた」と言っても、「全体を完全に証明している」と言うつもりはありません。しかし、リーマン仮説の本質的なところは証明できたと思うので、ひとまず公表してご批判を請いたいと思います。

複素数は慣れてなかったので、初めは戸惑いましたが、ようやく慣れてきました。いろいろ分析するうちに、複素数の階乗を見つけましたが、これは結構重要な発見ではないでしょうか。世紀の大発見だと自画自賛しているところです。　(^^)　最後は、ちょっと面倒臭くなったので、手を抜いて（ーーー間違っているわけではありません。ーーー）証明を完成させましたが、必要があるなら、その続きのところもいずれ証明したいと思っています。

例によって、勘違いや間違いが混入していることが多々あるので、皆様のご助言、ご指摘いただければ幸いです。「証明の概略」の前半は以前のと同じです。





第１部　　　　　　証明の概略


■　　　　リーマンの零点はk(x）で計算できる

まずは、最初の大前提から説明します。おそらくk(x)と言っても何のことか判らないでしょうから、再度k(x)から説明することにします。

k(x)とはゼータ関数のxが実数の時、x>1で収束する値のことです。　第５の広場参照のこと

k(2)=1.644934067、k(4)=1.082323234 などで、k(2)=pi^2/6, k(4)=pi^4/90, k(6)=pi^6/945, k(8)=pi^8/9450, となることが判っています。
これを、k(2)=su(2)*2*pi^2, k(4)=-su(4)*2^3*pi^4,　もしくは、k(2)=B(2)*pi^2*2/2!, k(4)=-B(4)*pi^4*2^3/4!, のように、su(r), B(r) を使っても表記できます。ベルヌーイ数はあちこちに顔を出します。
これをもっと一般化して数式化すると以下のようになります。
Σ1/n^r = k(r)-1/(r-1)/n^(r-1) + 1/2/n^r - r/12/n^(r+1) + 0 + r*(r+1)*(r+2)/6!/n^(r+3) + 0 + .....

この公式を使うと、k(x)を速やかに計算できます。x<1でも、x<0でも計算できます。たとえば、k(0)=-0.5 、k(0.5)=-1.4603545088... となります。

このk(x)に複素数を代入して計算すると、リーマンの零点を得ることが出来ます。リーマン自身の使った数式を知りませんし、その後のリーマン仮説の研究者の研究成果も知らないので、この式が彼らの式と同じかどうか判らないのですが、おそらく別の式ではないかと思います。しかし、計算上同じ結果になるのですから、これで良しとしていただかないことには話しになりません。以下の証明ではこのことは大前提となっています。


■　　　複素数における零点の法則

さて、複素数a+biが零であるとは、a=0 かつ b=0　ということです。そして、複素数zが零の時、任意の複素数x に対して、x*z=0 となり、x/z は計算不能となるのは実数の時と同じです。交換法則や結合法則も成り立ちます。そして、x*y=0 の時、　x=0　もしくはy=0　であることも実数と同じです。x≠0　かつ y≠0 のとき、x*y≠0 であることも実数と同じです。

また、(c+di)/(a+bi)において、a+bi=0なら、無限大になるというのが実数での結論ですが、複素数では、分子・分母に(a-bi)を掛けて、(c+di)*(a-bi)/(a^2+b^2)という形に導きます。分子は(ac+bd)+(ad-bc)*i となります。a+bi=0ですから、a=0, b=0 なので、分子も零となり、0/0という結論になります。ですから、必ずしも無限大になるとは限りません。

x^2も、実数ならば必ずプラスの値を取りますが、複素数ではx=a+bi ですから、x^2=(a^2-b^2)+2abi となり、マイナスになる可能性もあります。

なお、複素数の表記法ですが、a+bi のことを(a,b)と書くことも出来るとのことなので、適宜そのようにしたところもあるので、ご了解ください。


■　　　　　　複素空間で複素数の動きを調べる

実数関数ではXY座標を使って関数の形を調べます。私もXY座標の威力にほとほと感心した人間のひとりで、 これを発案したデカルトを深く尊敬しています。XY座標は、数学の本質を変えるものではありませんが、 これにより数学を判りやすくすると言うことにおいて絶大な貢献をはたしました。数学史の本を開けてみると、 このXY座標の発案についての記述があまりないのですが、これについては是非触れて欲しいと思います。

さて、XY座標と同じアイデアを複素数にも導入したいのですが、複素関数では、x、y のそれぞれにa, b という二つの要素があり、 合計４つの要素を考えなければなりません。しかし、平面で使えるのは２つ、空間として捉えても３つしか扱えません。 何かよい方法はないだろうかと模索しているのですが、なかなかこれと言ったものが見つかりません。やむを得ず、ここでは複素空間というアイデアを使うことにします。

複素空間は、XYZ座標と同じことですが、ただ、ふたつのXYZ座標を重ねて理解するという特徴があります。 つまり、複素関数のxには(a1, b1)という要素があるので、a1をX軸、b1をY軸として、平面全体をa1+b1*i と対応させます。 xが定まると、それに対応している平面上の点が定まることになります。 さて、yにもふたつの要素があるので、(a2, b2) と表現します。このa2とb2をZで対応させます。 つまり、yの実部であるa2を意味するZ座標と、虚部のb2を意味するZ座標のふたつを想定するのです。 これで、複素数x, y がXYZ座標と対応関係を持つことができるようになります。

ひとつの数にふたつの空間を想定するのはやや不便ですが、いまのところ仕方ありません。これを使って複素関数の姿をなんとか捉えてみたいと思います。


■　　　　　　リーマン零点とは


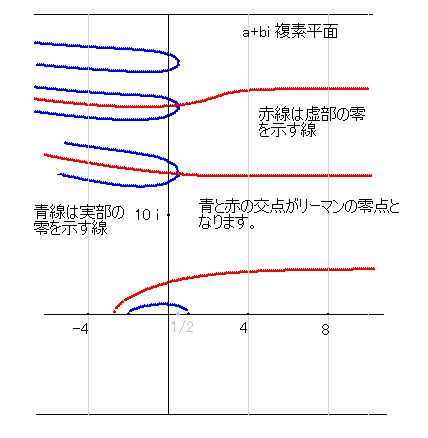
さて、k(x)を複素数に拡大して、x=a+bi 、k(x)=z1+z2*i と理解します。k(x)が零となるのが零点ですから、z1=0 かつ z2=0 ということです。これを視覚的に理解するために、まずはXYz1座標においてz1=0となるようなa, b を探してみます。そのようなa, b をXY座標で表し、複素平面図を描いてみます。また、XYz2座標でも同じようにz2=0となるような図を色を変えて描いてみます。 そのふたつを重ねたとき、その交点がz1=0, z2=0 となっているので、そこが零点であることが判ります。右図は、まだ未完成ですが、完成図が見たい方は「零点の計算方法」のページ
をご覧ください。完成図はあまりに線が多すぎるので、ここでは未完成の図のままにしておきます。この図を見ると、実部と虚部の交点がa=0.5の線上にあることが判ります。

零点は、b=0 つまり実数の線上にもあります。「それ以外に零点となるところがない」ということがリーマン仮説の内容ですから、それを証明することがここでの目標になります。



■　　　k(x)=f(x)*g(x)　となるf(x), g(x) を見つける

さて、リーマン仮説を証明する方法としては、k(x)=f(x)*g(x)　となるような f(x), g(x) を見つけるというやり方でゆきたいと思います。

実数の場合、z≠0を証明するためには、z=x*y の式に於いて、x≠0 かつ y≠0 を証明することになります。これをそのまま関数に応用し、f(x)とg(x)がともに、a=0.5, b=0 以外で零とならないことを証明すれば、それがそのままk(x)の証明となります。

そこで、k(x)=f(x)*g(x)となるf(x), g(x)を探したのですが、最初に見つけたのは、k(x)=zeta(x-0.5)*hk(x) という式でした。これは、zeta(x-0.5)も、hk(x)も綺麗な式に因数分解できるので、とても魅力的でしたが、証明としてはうまくいきませんでした。

そこで、さらに別の式を求めて彷徨ったのですが、zeta(x)はx<1で収束しないので、使うのを止めにしました。聞くところによると x>1、x<0 ではすでに証明が完了しているとのことなので、証明されていることをさらに証明してもあまり意味はありません。そこで、x<1で収束する式を見つけることが至上命令となりました。そういう方針のもとに探していると、k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } という式を見つけました。複素数の階乗はまだ定義されていませんが、k(x)は計算可能ですから、この式を複素数階乗の定義として使うことが出来ます。正しい定義なのかどうかはさらに検討が必要ですが、今のところ矛盾無く計算できるので、この証明では一応、これが正しいとの前提で進めさせていただきます。


■　　　x!(1-x)!に零点はない

階乗の定義を使うと、x!(1-x)!の式でk(x)を消すことが出来ます。

x!(1-x)! = (1-x)*x*pi / { 2*cos(pi(1-x)/2)*cos(pi*x/2) }

これを複素数に拡張して、x=a+biを代入します。これによりx!(1-x)!という式の複素空間を調べることが可能となります。その結果、a=0.5以外には零点がなさそうだということに気が付きます。これは、計算結果と言うより、上記の公式の右辺を見ると零点の無い式ばかりなので、この式を使って証明可能となります。つまり、cos((a+bi)*pi/2)に零点がないことを証明すればよいのです。

これでx!(1-x)!に零点がないことがわかります。しかし、x!に零点がないことはさらに次の証明が必要となります。


■　　　マイナスの階乗の公式

ここでマイナスの階乗の公式を使うことになります。これは私のHP「第４の広場の付録・　実数値での階乗の計算方法」で説明したことですが、(-n)!=n*pi/n!sin(n*pi) という公式があります。これは私が発見したので、（＾＾）　おそらくまだ知られていないと思いますが、これがリーマン証明に役立つとは思いもしませんでした。

これでx!に零点がないことが証明できます。

x!に零点がないとなれば、あとはcos(pi*x/2)と(2*pi)^xを証明して、その結果、k(1-x)/k(x)に零点がないことになります。


■　　　k(1-x)/k(x)に零点がない

「k(1-x)/k(x)は零点がないので、k(x)にも零点が無い」と言いたいのですが、そう簡単には言えません。k(1-x)が零のときはk(x)=0の可能性が残ります。ですから、k(1-x)が零にならない証明が必要となります。しかし、これはk(x)の証明と内実は同じことですから、堂々巡りとなります。

そこで、これについては、やや強引なやり方になりますが、a=0.5の近傍のみでの証明をすることにしました。x>1、x<0 についてはすでに証明が終わっているそうですし、「a=0.5の近傍以外には零点は存在しないことが証明された」とも聞きました。ですから、今回、a=0.5の近傍のみの証明となっても、何らかの意義があるのではないでしょうか。もし私の伝聞が間違っていて、まだ証明が終わっていないなら、続きの証明もトライするつもりでいます。

ということで、以下に証明の本体を載せておきます。間違いがあるなら訂正しますのでご指摘ください。







第２部　　　　　　証明の本体


■　　　　　　k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x }

k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } という式があります。この式は私が発見したので、疑い深い人には信じてもらえないかもしれませんが・・・、たしかに微妙なところがあります。なぜなら、この式の中に階乗があり、今の段階では複素数の階乗は定義されていないからです。しかし、左辺は複素数を代入して問題なく計算可能ですし、コサインもテーラー展開式を使うと計算可能となります。(2pi)^(a+bi)も計算できます。ですから、この式から複素数の階乗を計算できることになります。

まずは、この式がx<1の実数で成り立つことを計算結果で示しておきます。右辺をuhenとし、左辺をsahenとします。それぞれ別々の式で計算した結果が次のものです。x=a+biで、a=0.2, b=0 とするとき、
sahen=6.046344, uhen=6.046344 で、sahen/uhen=0.99999... となり、9が１００個ほど並びました。aがどの値でも誤差なしに値が出てきます。こういう場合は複素数に拡張することができます。

さて、右辺の式に零点が無ければ左辺にも無いことになります。そこで、それぞれどのようになっているか調べてみます。x!は面倒なので後ましにして、cos(pi*x/2)から調べます。


■　　　 cos(pi*x/2)

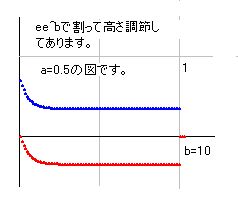
cos(pi*x/2)を複素数として計算するためにx=a+biとします。cos(x)=1-x^2/2+x^4/4!-x^6/6!... ですから、これにx=a+biを代入すると結果が出てきます。bが増加すると値が図からはみ出すので、その調整方法を探していると、ee=2.718281828として、ee^bで割ると収束することがわかりました。つまり、cos(a+bi)=z1+z2*i とし、p=ee^b とすると、z1/p, z2/p が一定の値になるということです。これで図は非常に単純化しました。実部も虚部も同時に零になることはないのはすぐに判ります。a=0.5のときの図を載せておきます。






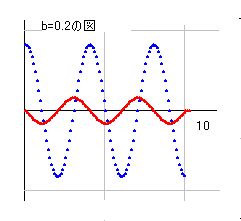
bを特定したときの形のほうが判りやすいので、そちらの図を使って説明すると、右図のように実部がコサイン曲線、虚部がサイン曲線として現れます。これはどのbの値に対しても同じです。









b=0.2とb=2の図を比較すると判りますが、高さが異なるだけのことで、同じ構造をしています。z=0との交点については実部と虚部が交互に現れるので、交わることはありません。また、b=0.2とb=2を重ねると判りますが、実部の交点どうしは同じ場所で重なっていて、虚部は虚部で重なっています。

実部と虚部がともに零となる点は、b=0のときだけであり、a=1, 3, 5, 7, 9 と規則正しく並んでいます。



■　　　 (2*pi)^x　の証明

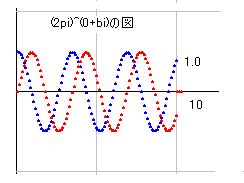
(2*pi)^x をx=a+biとして計算します。b=0のときが実数ですが、この場合、aの増加により(2*pi)^xは飛躍的に増加して図を描けません。そこで(2*pi)^a で割ることにしたところ、どのaに対しても同じ図になりました。右図はa=0のときのものですが、他の値でも同じ形になります。サイン曲線とコサイン曲線が綺麗に並んでいて、z=0で交わることはあり得ません。無限大になる点もありません。任意のbに対してaが変化する図を書いてみると、a軸に対して平行な線が出来ます。値の変化が無いと言うことですから、零点も無限点もありません。

この式の場合は、(0,0)でも零になっていません。


■　　　 x　の証明

x=a+bi ですから、a=0, b=0 のときが零点で、それ以外にはありません。


■　　　 x!　の証明 　　　(1-x)!*x! という式を使います。


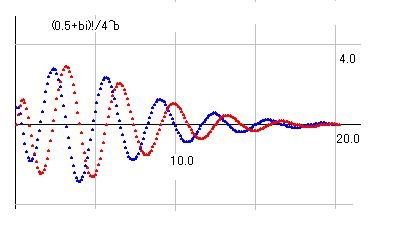
さて、x!の複素数定義が見つかったばかりで、まだその実態を充分に研究しているわけではありませんが、期待したほど綺麗な形にはなっていませんでした。右図はa=0.5のときのb=0から20までのグラフですが、r!の値をそのまま使うと図からはみ出してしまうので、4^bで割って、枠の中に収まるように高さ調整してあります。しかし、これだとb=20近くで値が零に近くなってしまうので、図としてはもうひと工夫必要なところです。いずれもっと綺麗な図になるように調整したいと思います。

ただ、図を工夫しても、実態は同じです。任意のaに対して、bが増加すると波を描きながら、値は比価級数的に増大します。波は一見同じように見えますが、細部に於いては複雑な動きをするところもあり、一筋縄ではいきません。これではk(x)の証明と同程度に難しそうという感想が生じてきます。

しかし、(1-x)!*x! という式を考えると、すべての問題は解消します。

x!= k(1-x)*x*(2pi)^x / { k(x)*2*cos(pi*x/2) } というのが、今回の証明の前提になっている複素数階乗の定義です。ですから、(1-x)!*x! もこの定義からすぐに導くことが出来ます。つまり、k(1-x)とk(x)が消えて、計算しやすい関数だけが残ります。
(1-x)!x! = (1-x)*x*pi /{ 2*cos(pi(1-x)/2)*cos(pi*x/2) }

分子の (1-x) と x は、それぞれa=1, b=0 で零、a=0, b=0 で零となります。分母の cos(pi*(1-x)/2) と cos(pi*x/2) はa=0.5を基準として左右対称の形をしているので、片方を分析すれば、もう片方も同じ結論になります。そこで、cos(pi*x/2)がどのようになっているかを調べてみます。


■　　　 cos(pi*x/2)

cos(pi*x/2)については先ほど説明したばかりなので、そちらを参照してください。bを特定して図を描くと、実部がコサイン曲線、虚部がサイン曲線となります。ですから、b=0を除き、z=0で交わることはありません。

実部と虚部がともに零となる点は、b=0のときだけであり、a=1, 3, 5, 7, 9 と規則正しく並んでいます。

■　　　 cos(pi*(1-x)/2)　の零点の場所

cos(pi*(1-x)/2)　はcos(pi*x/2)　と同じ構造ですから、零点の場所は、b=0のときだけで、a=0, 2, 4, 6 と続きます。

さて、(1-x)!x!　の零点を求めると書きましたが、あと証明のためには無限点の場所も含めて確認しておかなければなりません。それゆえ、(1-x)!x! の零点は、分子が零の(0,0), (1,0)のふたつで、無限点は、分母が零の(0,0), (1,0), (2,0), (3,0),... などの場所になります。



■　　　 x! の零点・無限点は？

さて、(1-x)!x!の零点・無限点の場所は確認できましたが、それがx!のすべての零点・無限点であると断言するわけにはいきません。なぜなら、その他の可能性がまだ排除されていないからです。

もし(1-x)!に無限点があったとすると、それに対応するx!の点が零であっても(1-x)!x!は有限な値を取ることがあります。ですから、(1-x)!に無限点がないことを証明しなければなりません。そこで、このことの証明のためにマイナスの階乗の公式を使うことにします。



■　　　 マイナスの階乗の公式

マイナスの階乗の公式とは、(-n)! = n*pi/n!sin(n*pi) というものです。これが実数の範囲で正しいことは、先のページ　「第４の広場の付録・　実数値での階乗の計算方法」　で説明してあります。ここではそれを複素数に拡張して使うことにします。x=a+bi として、 (-x)! = x*pi / x!sin(x*pi) という式になります。

先の分析から、b=0のときはsin(r*pi)が零になることもあります。そのときは(-x)!が無限大となります。事実、実数のマイナス階乗には繰り返し無限大が現れます。

さて、b=0以外のところではx!が零になることが無いことを背理法により証明します。

もし、b=0以外のところでx!が零になるところがあったとして、その点をx1=a1+b1iとします。この時、sin(x*pi)はb≠0なので、零にはなりません。すると、マイナスの公式から(-x1)!は必ず無限大となります。また一方で、(1-x)!x!の分析から、x1!が零の時は(1-x1)!が無限大でなければなりません。しかし、(1-x1)!が無限大と言うことは、マイナスの公式から(x1-1)!が零であることになります。そして、(x1-1)!が零なら、(1-x)!x!の分析から(2-x1)!が無限大でなければならなくなります。(2-x1)!が無限大なら、(x1-2)!は零で、(3-x1)!は無限大となります。この作業は際限なく続くので (-a1+1,b1), (-a1+2,b1), (-a1+3,b1) と並ぶ点は無限大に、(a1-1,b1), (a1-2,b1), (a1-3,b1) と並ぶ点は零になります。b1は零ではないので、虚数ということで、x!の複素数部分にたくさんの無限大点と零点が一直線に並ぶことになります。

これは起こりそうもないことですが、一応起こったとすると、これによりk(1-x)/k(x)にもたくさんの無限大と零点が生じることになります。x1!は零と仮定されているので、k(1-x1)/k(x1)=0となります。この場合、k(1-x1)=0 もしくは k(x1)=∞ ということで、それ以外の可能性はありません。また、(x1-1)!も零ですから、k(2-x1)=0 もしくはk(x1-1)=∞　となります。この並びは無限に続くことになり、ある特定のb1に対して、その列においては実部が1増減するたびに零点、もしくは無限大が現れることになります。ところが、a<0とa>1ではすでにどなたかが零点はないと証明していると聞いています。その証明のやり方については確認していませんが、一応それを前提にするなら、ここに矛盾が生じ、背理法の原理により最初の仮定である「b=0以外でx!が零になるところがある」という命題が間違っていたことになります。もし、a<0とa>1の証明がまだ未完成なら、いずれ私自身もその証明にトライするつもりなので、今は今後の課題として残しておきます。

そういうわけで、ここではk(x)がa<0で零点を持たないことを証明された命題として受け入れるので、x!にも零点がないことが証明されたことになります。（もちろんk(x)がa<0で零点を持たないことは直感的には証明する必要もないほど明らかであることは別ページで述べたとおりです。）




■　　　　　　k(1-x)/k(x) の零点の場所

これで　k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x }　の右辺にあるすべての項目を検討したことになります。右辺の式が b=0上以外で零にならないのですから、k(1-x)/k(x)も零にならないことになります。

ここでb=0上の零点の場所を再確認すると共に、それがk(1-x)/k(x)にどのように反映されているかを確認しておくことにします。

まずは、(1-x)!x! = (1-x)*x*p /{ 2*cos(pi(1-x)/2)*cos(pi*x/2) }　の式を再確認しますが、このとき、右辺の分母が零となるのが、b=0上のところだけで、a=0,1,2,.... とつづきます。ですから、(1-x)!x!では無限点となります。分子が零のところは、(0,0), (1,0) ところですが、分母が零なので、(1-x)!x!がどうなるかは不明です。

x!については、(0,0), (1,0) については、この式からはどうなるか不明ですが、一応特異点として扱うことにします。（実際は、0!=1, 1!=1 ということが判っています。）b=0とは実数ということですから、(-2)!, (-3)!,　... と見てゆくと、すべて無限大になることを示しています。これは、従来のマイナス階乗の理解と一致しています。

さて、k(1-x)/k(x)の右辺分母は x*(2*pi)^x ですが、零となるのは(0,0)だけです。

右辺分子の零点は、(-2,0),(-3.0),...と、(0,0),(1,0),(2,0),(3,0)... です。(0,0)では分母も零ですから、別途検討が必要です。それ以外はすべて零と言うことです。b=0上以外の点で零になるところはありません。

さて、ここで説明が必要ですが、k(x)の場合はa=0.5上に零点があることになっています。ところがk(1-x)/k(x)の右辺にはa=0.5上に零点も無限点もありません。証明とは直接関係ありませんが、a=0.5の零点がどこから来るかを説明しておくことにします。

k(1-x)/k(x)はa=0.5を基準に対照で、a=0.5では同じ値どおしを割ることになり、必ず(1,0)という答えになることが初めから定められています。問題は、このk(x)の特徴としてa=0.5上に零点があることです。この零点においては、0/0ということになり、特異点となるのですが、右辺ではそれが解消されて見えなくなっています。つまり、右辺の計算上ではその点における答えは (0.5,b1)/(0.5,b1)=(1,0) ということです。ですから、右辺が零でない場所でも、左辺のk(x)が零になることがあるということです。



■　　　　　　k(1-x)/k(x)≠0のとき、k(x)≠0を証明します。



「 b=0上 以外のところでは k(1-x)/k(x)≠0 かつ k(1-x)/k(x)≠∞」 が証明できました。「それならk(x)は零でない」と言いたいところですが、k(1-x)=0のときはk(x)=0の可能性が残っています。事実、a=0.5で、k(1-x1)=0 かつ k(x1)=0 となるx1が存在しますが、k(1-x1)/k(x1)≠0となっています。ですから、ここではa≠0.5という条件を付けて、k(1-x)≠0の証明を追加しなければなりません。しかし、k(1-x)とk(x)は基本的には同じ式ですから、「k(1-x)を証明するためにk(x)を証明する」という堂々巡りとなってしまいます。これではうまくいきません。


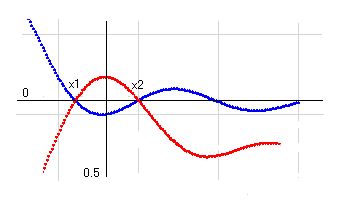
そこで、k(x), k(1-x)を纏めて零でないことを証明することにします。a≠0.5という条件で、k(x1)=0, k(1-x1)=0となるx1が存在したとします。すると、k(x)において、a=0.5を軸として左右等距離のところに零点が存在することになります。そこはa≠0.5ですが、k(1-x1)=0 かつ k(x1)=0 が成り立っています。そのときのk(x)の図は右のようになっているはずです。実部線も虚部線もx1とx2の間に、必ず波の山か谷を挟んでいなければなりません。そうでないと２つの零点を持つことが出来ないからです。


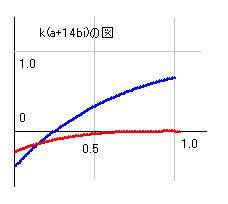
しかし、実際のk(x)の図を調べてみると、a=0.5の近傍にはこのような山とか谷が現れることはまれなことです。たとえば、k(a+14i)の図を見ると、a=0から1までのところで実部も虚部も単調に増加していて、波の山谷はありません。このようなとき、実部も虚部もz=0と交わるとしても一点だけであり、２点で交わることは不可能です。bの値を変えてもa=0.5の近傍では単調に増加・減少するということについては変わりありません。ときには山や谷が現れることもあるのですが、その場合も、実部に波があるときは虚部が単調であるとか、虚部に波が現れるときは実部が単調であるなどして、両方とも波になることはまずありません。ですから、このようなa=0.5の近傍には零点がないことは証明できたと言えるのではないでしょうか。

もっとも、波の山谷がまったく無いというわけではないので、この証明には限界があります。しかし、ひとまずこのあたりで区切りをつけたいので、ここまでの証明で明らかになったことを確認しておきます。

a=0.5を基準として、その左右に生じる実部線、虚部線が、単調に増加、もしくは減少しているなら、その範囲内には零点は存在しないということは明らかです。そこまでは証明できたものと考えたいと思います。残りのところは、今後さらに検討する予定です。



ここまでの証明の中で間違いや問題点があるならご指摘いただけると幸いです。

ご感想、ご質問、その他のご意見は、以下のアドレスまでお寄せください。