リーマン仮説（リーマン予想）の証明 ver8.0
証明はまだ完成していませんが、先の証明（ver 5）よりは一歩前進したので、ここで公表して、多くの方々からのご意見、ご批判をいただきたいと思います。
先の証明には、用語法や定義などについて自分勝手なところがあったようなので、それについては全部修正したつもりです。まだ問題点が残っているかもしれませんが、証明の是非に直結しないところでは順次訂正してゆきます。証明に関わるところで間違えているなら、この証明を取り消して、再度チャレンジするつもりです。どのような点であれ、ご指摘いただければ幸いです。
第１部 証明の概略
■ リーマンの零点はk(r）で計算できる
私自身の研究の過程で見つけたk(r)という関数があります。先の証明（ver5）では、Σ(1/n^r)をゼータ関数と呼んで、k(r)はその部品と説明しましたが、その説明は間違いだとの指摘を受けました。どうもk(r)のほうがゼータ関数と定義されているようです。私自身はまだそれに納得できないのですが、数学者の方々がそのように定義しているなら、それを否定するわけにもいきません。やむを得ないので、これからはその点にも留意して解説することにします。誤解を避けるために、以下の説明ではゼータ関数という言い方はなるべく避けることにしました。もし、ゼータ関数という言葉があったほうが判りやすいなら、このk(r)をゼータ関数と理解してお読みいただければと思います。
k(r)とは第５の広場で説明してありますが、Σ1/n^r = 1 + 1/2^r + 1/3^r + 1/4^r + .... + 1/n^r において、 r>1 （rは正の整数）、n→∞で収束する値のことです。
このrが偶数の時、k(r)はpiと有理数で表記できます。つまり、k(2)=1.644934067、k(4)=1.082323234 などで、k(2)=pi^2/6, k(4)=pi^4/90, k(6)=pi^6/945, k(8)=pi^8/9450, となります。
これを、k(2)=su(2)*2*pi^2, k(4)=-su(4)*2^3*pi^4, もしくは、k(2)=B(2)*pi^2*2/2!, k(4)=-B(4)*pi^4*2^3/4!, のように、su(r), B(r) を使って書くこともできます。ベルヌーイ数はあちこちに顔を出します。
このrを実数に拡張してxとすると、以下のように書くことが出来ます。
Σ1/n^x = k(x)-1/(x-1)/n^(x-1) + 1/2/n^x - x/12/n^(x+1)
+ 0 + x*(x+1)*(x+2)/6!/n^(x+3) + 0 + .....
この公式を使うと、k(x)を速やかに計算できます。x<1でも、x<0でも計算できます。たとえば、k(0)=-0.5 、k(0.5)=-1.4603545088... となります。
このk(x)を複素数に拡張してs=a+bi とすると、
Σ1/n^s = k(s)-1/(s-1)/n^(s-1) + 1/2/n^s - s/12/n^(s+1)
+ 0 + s*(s+1)*(s+2)/6!/n^(s+3) + 0 + .....
となり、これでリーマンの零点を計算することが出来ます。リーマン自身の使った数式を知りませんし、その後のリーマン仮説の研究者の研究成果も知らないので、この式が彼らの式と同じかどうか判らないのですが、計算上同じ結果になるのですから、これで良しとしていただかないことには話しになりません。以下の証明ではこのことは大前提となっています。
なお、Σ1/n^sをzt(s,n)と表記し、-1/(s-1)/n^(s-1)以下の式に-1を掛けたもの、つまり符号を変えた式をber(s,n)と表記することにします。ですから、 k(s)=zt(s,n)+ber(s,n) となります。
■ 複素数における零点の法則
さて、複素数a+biが零であるとは、a=0 かつ b=0 ということです。そして、複素数zが零の時、任意の複素数x に対して、x*z=0 となり、x/z は計算不能となるのは実数の時と同じです。交換法則や結合法則も成り立ちます。そして、x*y=0 の時、 x=0 もしくはy=0 であることも実数と同じです。x≠0 かつ y≠0 のとき、x*y≠0 であることも実数と同じです。
また、(c+di)/(a+bi)において、a+bi=0なら、無限大になるというのが実数での結論ですが、複素数では、分子・分母に(a-bi)を掛けて、(c+di)*(a-bi)/(a^2+b^2)という形に導きます。分子は(ac+bd)+(ad-bc)*i となります。a+bi=0ですから、a=0, b=0 なので、分子も零となり、0/0という結論になります。ですから、必ずしも無限大になるとは限りません。
x^2も、実数ならば必ずプラスの値を取りますが、複素数ではx=a+bi ですから、x^2=(a^2-b^2)+2abi となり、マイナスになる可能性もあります。
なお、複素数の表記法ですが、a+bi のことを(a,b)と書くことも出来るとのことなので、適宜そのようにしたところもあるので、ご了解ください。
■ 複素空間で複素数の動きを調べる
実数関数ではXY座標を使って関数の形を調べます。私もXY座標の威力にほとほと感心した人間のひとりで、これを発案したデカルトを深く尊敬しています。XY座標は、数学の本質を変えるものではありませんが、これにより数学を判りやすくすると言うことにおいて絶大な貢献をはたしました。数学史の本を開けてみると、このXY座標の発案についての記述があまりないのですが、これについては是非触れて欲しいと思います。
さて、XY座標と同じアイデアを複素数にも導入したいのですが、複素関数では、x、y のそれぞれにa, b という二つの要素があり、合計４つの要素を考えなければなりません。しかし、平面で使えるのは２つ、空間として捉えても３つしか扱えません。何かよい方法はないだろうかと模索しているのですが、なかなかこれと言ったものが見つかりません。やむを得ず、ここでは複素空間というアイデアを使うことにします。
複素空間は、XYZ座標と同じことですが、ただ、ふたつのXYZ座標を重ねて理解するという特徴があります。つまり、複素関数のxには(a1, b1)という要素があるので、a1をX軸、b1をY軸として、平面全体をa1+b1*i と対応させます。xが定まると、それに対応している平面上の点が定まることになります。さて、yにもふたつの要素があるので、(a2, b2) と表現します。このa2とb2をZで対応させます。つまり、yの実部であるa2を意味するZ座標と、虚部のb2を意味するZ座標のふたつを想定するのです。これで、複素数x, y がXYZ座標と対応関係を持つことができるようになります。
ひとつの関数にふたつの空間を想定するのはやや不便ですが、いまのところ仕方ありません。これを使って複素関数の姿をなんとか捉えてみたいと思います。
■ リーマン零点とは
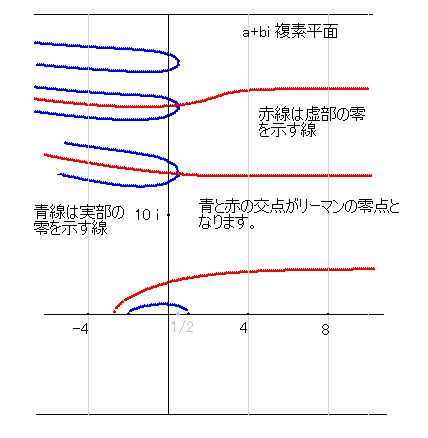
さて、k(x)を複素数に拡大してk(s)とし、s=a+bi 、k(s)=z1+z2*i と理解します。k(s)が零となるのが零点ですから、z1=0 かつ z2=0 ということです。これを視覚的に理解するために、まずはXYz1座標においてz1=0となるようなa, b を探します。そのようなa, b をXY座標で表し、複素平面図を描いてみます。これを実零線と名付けます。また、XYz2座標でも同じようにz2=0となるような図を色を変えて描いてみます。これを虚零線と名付けます。
そのふたつを重ねたとき、その交点がz1=0, z2=0 となっているので、そこが零点であることが判ります。右図は、まだ未完成ですが、完成図が見たい方は「リーマン仮説を納得する方法」のページをご覧ください。完成図はあまりに線が多すぎるので、ここでは未完成の図のままにしておきます。この図を見ると、実部と虚部の交点がa=0.5の線上にあることが判ります。
零点は、b=0 つまり実数の線上にもあります。「それ以外に零点となるところがない」ということがリーマン仮説の内容ですから、それを証明することがここでの目標になります。
なお、複素数においては、実部が零となる点と虚部が零となる点があり、それらを零点と呼ぶこともあるのですが、この証明ではそれぞれ「実部の零点」、「虚部の零点」と呼び、どちらも零のところは「零点」もしくは「リーマンの零点」と呼んで区別しています。ただ、文脈上明らかなときは「実部のみの零点」を「零点」と呼ぶこともありますので、そのあたりは臨機応変に解釈していただければと思います。
■ k(s)=f(s)*g(s) となるf(s), g(s) を見つける
さて、リーマン仮説を証明する方法としては、k(s)=f(s)*g(s) となるような f(s), g(s) を見つけるというやり方でゆきたいと思います。
実数の場合、z≠0を証明するためには、z=x*y の式に於いて、x≠0 かつ y≠0 を証明することになります。これをそのまま関数に応用し、f(x)とg(x)がともに、a=0.5, b=0 以外で零とならないことを証明すれば、それがそのままk(x)の証明となります。複素数関数でも同じことです。
そこで、k(s)=f(s)*g(s)となるf(s), g(s)を探したのですが、最初に見つけたのは、k(s)=zt(s-0.5)*hk(s) という式でした。
zt(s-0.5)=Σ(1/n^(s-0.5) で、 hk(s) = 1 + (√2-1)/2^s + (√3-1)/3^s - (√2-2)/4^s + (√5-1)/5^s + ... という式です。
これは、zt(s-0.5)も、hk(s)も綺麗な式に因数分解できるので、とても魅力的でしたが、証明としてはうまくいきませんでした。
■ k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x }
そこで、さらに別の式を求めて彷徨ったのですが、zt(s)はs<1で収束しないので、使うのを止めにしました。証明のためには s<1 で収束する式を見つけなければなりません。そういう方針のもとに探していると、k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } という式を見つけました。複素数の階乗については、私自身何も知りませんが、k(s)は計算可能ですから、この式を複素数階乗の定義として使うことが出来ます。正しい定義なのかどうかはさらに検討が必要ですが、今のところ矛盾無く計算できるので、この証明では一応、これが正しいとの前提で進めさせていただきます。
■ k(1-s)/k(s)に零点がない
この式を使ってk(1-s)/k(s)≠0を証明することができます。途中で、マイナス階乗の公式などを使いますが、これについては「証明の本体」を参照してください。
ここから先が難関です。「k(1-s)/k(s)は零点がないので、k(s)にも零点が無い」と言いたいのですが、そう簡単には言えません。k(1-s)が零のときはk(s)=0の可能性が残ります。ですから、k(1-s)が零にならない証明が必要となります。しかし、これはk(s)の証明と内実は同じことですから、堂々巡りとなります。
■ k(s)=0 なら、零点は３つになる
そこで、実虚線、虚実線と名付ける線を分析することにします。実虚線とは実零線の上の虚部の値のことです。実零線上の実部は零ですが、虚部は別の値をとっています。この値をzとして、Xz座標に表したものが実零線上の虚部ということで、実虚線と呼ぶことにします。虚実線とは、虚零線上の実部の値をzとして、それをXz座標に表したものです。
k(s)=0 なら k(1-s)=0となります。つまり、a=0.5を基点として等距離の所に零点が発生することになります。つまり、実虚線にも虚実線にも零点がふたつ発生することになります。しかし、ふたつということはあり得ず、「ふたつあるなら３つある」ことを示すことが出来ます。しかも、この３つの零点のうち、ひとつは必ずa=0.5上になければなりません。
■ k(s)の波の構造から、0<a<1 に零点が３つも存在することはないことを証明します。
零点が３つあるということは、うねりのある波がひとつ存在すると言うことです。ところが 0<a<1 かつ b>1 において、k(s)の図に波が発生することはありません。そのことを式の形から証明できると考えていますが、これについてはまだ完成していません。一応、ここまでのところを公表して、残りはまた後日、証明を完成させてから発表したいと思います。
以上の証明の概略にある程度納得した方は、以下の証明の本体を見ていただければと思います。
第２部 証明の本体
■ k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x }
k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } という式があります。この式は私が最初に発見したと思ったのですが・・・、すでに知られている式とのことで、少し残念です。しかし、それならそれで差し支えありません。複素数の階乗もガンマー関数で定義されているとのことですが、この点はまだ学びが足りないのでよく理解していません。ただ、この証明では上記の式を複素数の階乗の定義として使うことにしました。いまのところそれで何ら矛盾を起こすことはないので、問題ないと思いますが、もし、この点について間違っているなら、訂正しますので、教えていただければと思います。
さて、上記の式が正しいことはすでに承認されているとのことなので、ただちにこれを複素数に拡張して使うことにします。s=a+biとすると、
k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s }
となります。この式の右辺に零点が無ければ左辺にも無いことになります。そこで、右辺の式を個別に検討することにします。
■ cos(pi*s/2)
cos(pi*s/2)を複素数として計算するということは、cos(s)=1-s^2/2+s^4/4!-s^6/6!...
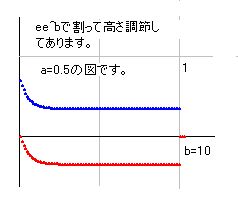
を計算すると言うことです。これをそのまま図示すると、bの増加に伴いすぐに値が図からはみ出してしまいます。そこで、e=2.718281828として、e^bで割ることにしました。cos(pi*s/2)=z1+z2*i とし、p=e^b とすると、z1/p, z2/p が極大化せず、一定の値に収束します。これで図は非常に単純化します。a=0.5のときの図を載せておきます。
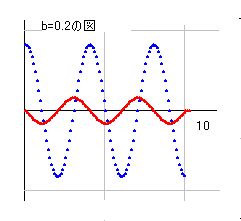
bを特定したときの形のほうが判りやすいので、そちらの図を使って説明すると、右図のように実部がコサイン曲線、虚部がサイン曲線として現れます。これはどのbの値に対しても同じです。
b=0.2とb=2の図を比較すると判りますが、高さが異なるだけのことで、同じ構造をしています。z=0との交点については実部と虚部が交互に現れるので、交わることはありません。また、b=0.2とb=2を重ねると判りますが、実部の交点どうしは同じ場所で重なっていて、虚部は虚部で重なっています。
実部と虚部がともに零となる点は、b=0のときだけであり、a=1, 3, 5, 7, 9 と規則正しく並んでいます。
■ (2*pi)^x の証明
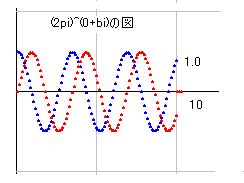
(2*pi)^s をs=a+biとして計算します。b=0のときが実数ですが、この場合、aの増加により(2*pi)^sは飛躍的に増加して図を描けません。そこで(2*pi)^a で割ることにしたところ、どのaに対しても同じ図になりました。右図はa=0のときのものですが、他の値でも同じ形になります。サイン曲線とコサイン曲線が綺麗に並んでいて、z=0で交わることはあり得ません。無限大になる点もありません。任意のbに対してaが変化する図を書いてみると、a軸に対して平行な線が出来ます。値の変化が無いと言うことですから、零点も無限点もありません。
この式の場合は、(0,0)でも零になっていません。
■ s の証明
s=a+bi ですから、a=0, b=0 のときが零点で、それ以外にはありません。
■ s! の証明 (1-s)!*s! という式を使います。
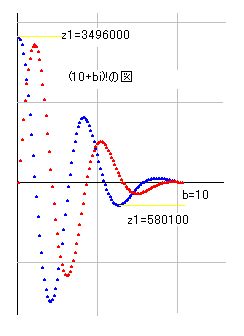
さて、s!はk(1-s)/k(s)を使って計算できます。その結果、s!の形がある程度判るのですが、期待したほど綺麗な形にはなっていませんでした。右図はa=10のときのb=0から10までのグラフですが、s!の値が巨大になっています。aの値を変えるとまた別の図になります。ですから、s!の実態を理解するのは結構面倒です。この図の場合は、bを増加させると波を描きながら小さくなっています。細部においては複雑な動きをする箇所もあり一筋縄ではいきません。これではk(s)の証明と同程度に難しそうという感想が生じてきます。
しかし、(1-s)!*s! という式を考えると、すべての問題は解消します。
s!= k(1-s)*s*(2pi)^s / { k(s)*2*cos(pi*s/2) } というのが、今回の証明の前提になっている複素数階乗の定義です。ですから、(1-s)!*s! もこの定義からすぐに導くことが出来ます。つまり、k(1-s)とk(s)が消えて、計算しやすい関数だけが残ります。
(1-s)!s! = (1-s)*s*pi /{ 2*cos(pi(1-s)/2)*cos(pi*s/2) }
分子の (1-s) と s は、それぞれa=1, b=0 で零、a=0, b=0 で零となります。分母のcos(pi*(1-s)/2)とcos(pi*s/2)はa=0.5を基準として左右対称の形をしているので、片方を分析すれば、もう片方も同じ結論になります。そこで、cos(pi*s/2)がどのようになっているかを調べてみます。
■ cos(pi*s/2)
cos(pi*s/2)については先ほど説明したばかりなので、そちらを参照してください。bを特定して図を描くと、実部がコサイン曲線、虚部がサイン曲線となります。ですから、b=0を除き、z=0で交わることはありません。
実部と虚部がともに零となる点は、b=0のときだけであり、a=1, 3, 5, 7, 9 と規則正しく並んでいます。
■ cos(pi*(1-s)/2) の零点の場所
cos(pi*(1-s)/2) はcos(pi*s/2) と同じ構造ですから、零点の場所は、b=0のときだけで、a=0, 2, 4, 6 と続きます。
さて、(1-s)!s! の零点を求めると書きましたが、あと証明のためには無限点の場所も含めて確認しておかなければなりません。分子が零なのは、(0,0), (1,0)のふたつで、分母が零なのは、(0,0), (1,0), (2,0), (3,0),... などの場所になります。(0,0)と(1,0)は、0/0ですから特異点となります。あとの(2,0), (3,0)... などは無限点となります。このことから、b≠0には零点も無限点もないことが判ります。
■ s! の零点・無限点は？
さて、(1-s)!s!の零点・無限点の場所は確認できましたが、それがs!の零点・無限点であると断言するわけにはいきません。なぜなら、その他の可能性がまだ排除されていないからです。
b≠0では必ず (1-s)!s!≠0 かつ (1-s)!s!≠∞ ですが、もし(1-s)!=∞ かつ s!=0 だと (1-s)!s!が零以外の有限値を取ることがあります。ですから、s≠0を証明するためには、(1-s)!が無限でないことの証明を追加しなければなりません。そこで、このことの証明のためにマイナスの階乗の公式を使うことにします。
■ マイナスの階乗の公式
マイナスの階乗の公式とは、(-n)!=n*pi/n!sin(n*pi) というものです。これが実数の範囲で正しいことは、先のページ 「第４の広場の付録・ 実数値での階乗の計算方法」 で説明してあります。ここではそれを複素数に拡張して使うことにします。s=a+bi として、
(-s)! = { s*pi } / { s!*sin(s*pi) }
という式になります。
■ sin(s*pi)の検討
右辺の中でsin(s*pi)はまだ検討していなかったので、ここでどこに零点が現れるかを見てみます。
sinの図はcosと同じ形で、X軸に平行に波が現れ、Y軸に平行に増加曲線が現れます。その増加は激しいのですが、e^bで割ると収束します。a=2.1のとき、b=0からb=10までを図示すると右のようになります。これは、実部も虚部もe^bで割った値を使っています。
b=2のとき、a=0からa=10までを図示すると、右のようになります。これもe^bで割っています。
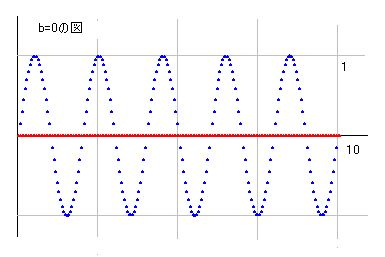
結局、実部、虚部ともに零となるのはb=0の場合のみで、a=1, 2, 3, 4... と零点が並びます。
sinが零点だと(-s)!が無限大になる可能性があります。面白いことに・・・というか、当然のことですが、実数のマイナス階乗には繰り返し無限大が現れるのと対応しています。
■ s!≠0 の証明
さて、b=0以外のところではs!が零になることも、無限になることもないことを背理法により証明します。
もし、b≠0という前提で、s!=0となるところがあると仮定し、その点をs1=a1+b1i とします。この時、sin(s1*pi)はb1≠0なので、零にはなりません。すると、マイナスの公式から(-s1)!は必ず無限となります。また一方で、(1-s)!s!の分析から、s1!が零の時は(1-s1)!が無限でなければなりません。しかし、(1-s1)!が無限と言うことは、マイナスの公式から(s1-1)!が零であることになります。そして、(s1-1)!が零なら、(1-s)!s!の分析から(2-s1)!が無限でなければならなくなります。(2-s1)!が無限なら、(s1-2)!は零で、(3-s1)!は無限となります。この作業は際限なく続くので (-a1+1,b1), (-a1+2,b1), (-a1+3,b1) と並ぶ点は無限に、(a1-1,b1), (a1-2,b1), (a1-3,b1) と並ぶ点は零になります。b1は零ではないので、虚数ということで、s!の複素数部分にたくさんの無限点と零点が一直線に並ぶことになります。
これは起こりそうもないことですが、一応起こったとすると、これによりk(1-s)/k(s)にもたくさんの無限点と零点が生じることになります。s1!は零と仮定しているので、k(1-s1)/k(s1)=0となります。この場合、k(1-s1)=0 もしくは k(s1)=∞ ということで、それ以外の可能性はありません。また、(s1-1)!も零ですから、k(2-s1)=0 もしくはk(s1-1)=∞ となります。この並びは無限に続くことになり、ある特定のb1に対して、その列においては実部が1増減するたびに零点、もしくは無限点が現れることになります。
ところが、以下に示すように、k(a+bi)=z1+z2*i において、lim_[a→∞]z1=1 となり、a>2においてk(s)は零になりません。つまり、k(2-s1)=0, k(3-s1)=0, k(4-s1)=0 ということが無限に続くことはありえないので、ここに矛盾が生じます。これで、背理法の原理により、最初の仮定である「b=0以外でs!が零になるところがある」という命題が間違っていたことになります。
なお、s!が零にならない証明と同様の方法で、s!が無限にならないことも証明できます。s!が無限ならば、k(2-s1)=∞、k(3-s1)=∞、k(4-s1)=∞ となり、limg_[a→∞]k(s)=1 と矛盾するからです。（b=0を除いています。）
■ limg_[a→∞]k(s)=1 を証明します。
xを実数としたとき、lim_[x→∞]k(x)=1 であることは自明のことと言ってもよいでしょう。これを複素数としても同じことなのですが、一応証明しておくことにします。
s=a+bi として、a>1のときk(a+bi)=z1+z2*i とします。すると、z1 = 1+Σ_[n=2,∞]cos(b*ln(n))/n^a および z2 = -Σ_[n=2,∞]sin(b*ln(n))/n^a が成り立ちます。cos(b*ln(n))=<1ですから、cos(b*ln(n))/n^a =< 1/n^a です。同じく、sin(b*ln(n))=<1ですから、sin(b*ln(n))/n^a =< 1/n^a です。
lim_[a→∞]1+Σ_[n=2,∞]1/n^a=1 および lim_[a→∞]Σ_[n=2,∞]1/n^a=0 が成り立つので、lim_[s→∞]k(s)=1 が証明できました。
ちなみに、Σ_[n=0,∞]1/n^2=1.6449...であることは良く知られています。cos(b*ln(n))=>-1ですから、a=2とすると、z1 >(1-0.6449) となり、z1>0となります。つまり、a=2においてk(s)≠0ということです。同じように、a=4のとき、k(4)=1.0823... ですから、z1>(1-0.0823) で、k(s)≠0, a=6でもk(s)≠0を示すことが出来ます。
また、cos(b*ln(n))=<1ですから、a=2とすると、z1 <1.645 となり、k(2+bi)≠∞ということになります。同じように、a=4のとき、z1<1.0824 で、k(4+bi)≠∞ となります。
■ k(1-s)/k(s) の零点の場所
これで k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } の右辺にあるすべての項目を検討したことになります。右辺の式が b=0上以外で零にならないのですから、k(1-s)/k(s)も零にならないことになります。
ここでb=0上の零点の場所を再確認すると共に、それがk(1-s)/k(s)にどのように反映されているかを確認しておくことにします。
まずは、(1-s)!s! = (1-s)*s*p /{ 2*cos(pi(1-s)/2)*cos(pi*s/2) } の式を再確認しますが、このとき、右辺の分母が零となるのが、b=0上のところだけで、a=0,1,2,.... とつづきます。ですから、(1-s)!s!では無限点となります。分子が零のところは、(0,0), (1,0) ところですが、分母が零なので、(1-s)!s!がどうなるかは不明です。
s!については、(0,0), (1,0) については、この式からはどうなるか不明ですが、一応特異点として扱うことにします。（実際は、0!=1, 1!=1 ということが判っています。）b=0とは実数ということですから、(-2)!, (-3)!, ... と見てゆくと、すべて無限大になることを示しています。これは、従来のマイナス階乗の理解と一致しています。
さて、k(1-s)/k(s)の右辺分母は s*(2*pi)^s ですが、零となるのは(0,0)だけです。
右辺分子の零点は、(-2,0),(-3.0),...と、(0,0),(1,0),(2,0),(3,0)... です。(0,0)では分母も零ですから、別途検討が必要です。それ以外はすべて零と言うことです。b=0上以外の点で零になるところはありません。
さて、ここで説明が必要ですが、k(s)の場合はa=0.5上に零点があることになっています。ところがk(1-s)/k(s)の右辺にはa=0.5上に零点も無限点もありません。証明とは直接関係ありませんが、a=0.5の零点がどこから来るかを説明しておくことにします。
k(1-s)/k(s)はa=0.5を基準に対照で、a=0.5では同じ値どおしを割ることになり、必ず(1, 0)という答えになります。問題は、このk(s)の特徴としてa=0.5上に零点があることです。この零点においては、0/0ということになり、特異点となるのですが、右辺ではそれが解消されて見えなくなっています。つまり、右辺の計算上ではその点における答えは (0.5, b1)/(0.5, b1)=(1, 0) ということです。ですから、右辺が零でない場所でも、左辺のk(s)が零になることがあるということです。
■ k(1-s)/k(s)≠0のとき、k(s)≠0を証明します。
さて、k(1-s)/k(s)≠0 が証明できたと言うことは、リーマン仮説証明の半分くらいが出来たと言うことを意味します。そこで、k(1-s)/k(s)≠0 を前提に残りの半分を証明することにします。
k(1-s)/k(s)≠0 であるからと言って、ただちにk(s)≠0 と結論を出すわけにはいきません。なぜなら、k(1-s)=0 のとき、k(s)=0である可能性があるからです。そこで、このふたつを一緒に証明することにします。つまり、k(1-s)≠0 かつ k(s)≠0 を纏めて証明します。
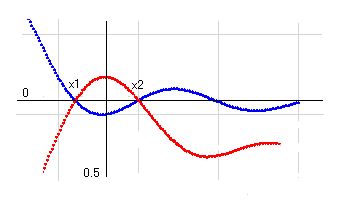
まずは背理法の仮定として、a≠0.5という条件で、k(s1)=0, k(1-s1)=0となるs1が存在したとします。すると、k(s)において、a=0.5を軸として左右等距離のところに零点が存在することになります。そのときのk(s)の図は右のようになっているはずです。実部線も虚部線もx1とx2の間に、必ず波の山か谷を挟んでいなければなりません。そうでないと２つの零点を持つことが出来ないからです。
このように、k(1-s)/k(s)≠0が成り立ち、かつk(s)=0であるなら、必ず零点がふたつ存在することになります。そして、a=0.5の近傍で、x1とx2の間には波の山か谷が必ず存在することになります。
ここまでのところもだいぶ修正しましたが、以下がver 8 で、おもに新しく付加した部分です。
■ k(s)=0とすると、零点が３つ存在することになる
さて、零点の数が２つだと、もうひとつの零点が存在しなければならないことを証明します。その後で、そのような波を持つk(s)が存在しないことを証明します。
零点がふたつだと矛盾が生じます。それを示すために実虚線、虚実線を定義し、その図を描いてみることにします。
実虚線とは、先の実零線を描いた図で、実零線上の虚部の値をグラフにしたものです。虚実線とは、虚零線上で実部の値をグラフにしたものです。
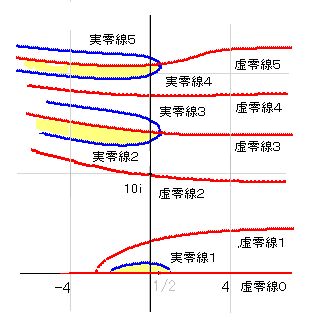
複素平面上にたくさんの実零線、虚零線がありますが、今回はb軸（Y軸）と交差する線だけを考察の対象にして、その線に番号を付けます。b=0から数えて最初の実零線を実零線１，２番目を実零線２と名付けます。虚零線も同じですが、b=0上にも虚零線があります。これは特殊なので虚零線０としておきます。０より大きいところを通る虚零線を１とします。次のを虚零線２，３番目を虚零線３とします。
すると、実零線は２番目と３番目が繋がっていて、４番目と５番目も繋がっていることが判ります。また、実零線の片側がプラスで、もう片方がマイナスで、横U字の中側がマイナス、外側がプラスであることは、計算してみるとすぐに判ります。
虚零線では１までがマイナス、２までがプラス、３までがマイナスと、交互に続きます。
判りやすくするために、実部も虚部もマイナスである部分を黄色で示しておきます。
■ 実虚線と虚実線
さて、実零線上では、実部は当然零ですが、虚部は別の値を取っています。この点がk(s)を示しているのですが、この線は立体的にくねくねと曲がっていて、そのまま理解するのは容易ではありません。そこで、これをa軸（X軸）から眺めて、投影した図を描くことにします。点と点のb軸上の距離は違っていますが、a軸に対する関係はそのままです。この作業によりできた線を、実零線上の虚部の値なので、実虚線と呼ぶことにします。
実零線１上の実虚線を実虚線１，実零線２上の線を実虚線２と名付けます。
実虚線２と実虚線３は繋がっているので、右図ではひとつの線として描かれています。
実虚線が零のところがリーマンの零点になります。そのことをはっきりさせるために図を拡大しておきます。
マイナス部分は実虚線２で、a=0.5で零を通過しているのが判ります。しばらく増加したのち、-aの方向に戻り始めます。この部分が実虚線３です。
実虚線４と実虚線５も繋がっています。その図は大まかには実虚線２，３と大差ありませんが、リーマンの零点の場所が上側の線（実虚線５）上に来ているのが相違点です。
虚零線についても同じ分析が可能です。虚零線上は虚部が零となっていますが、そこでの実部の値を平面的に捉えるとひとつの線ができあがります。それを虚実線と名付けます。各虚零線にひとつの虚実線が対応しているので、これに番号を付けます。虚零線は０番もあるので、虚実線にも０番を作ります。そして、虚零線１に対応するのが虚実線１，その次が虚実線２となります。
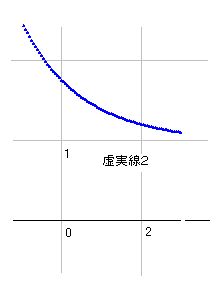
虚零線１、２、４は実部がプラスの部分だけを通っているので、虚実線はすべてプラスとなります。虚実線２の図を載せておきます。
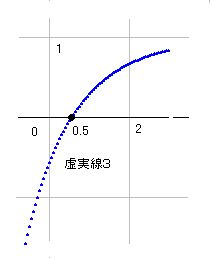
虚実線３，５は実部がマイナスからプラス１へと向かうので、必ずリーマン零点が発生します。虚実線３を載せておきます。虚実線５も３と大差ありません。
虚零線６と７は繋がっていて、また別の形をしています。ですから、それに対応する虚実線も別の形になります。ただ、以下の分析の結果に影響を与えるものではないので、図示するのは割愛します。
■ 零点がふたつだと虚実線に矛盾が生じます。
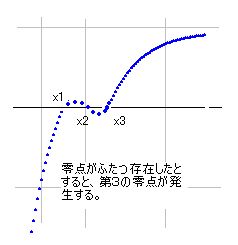
さて、先にk(1-s)/k(s)≠0を証明しました。それゆえ、もしk(s)=0とするなら、k(1-s)も零でなければならず、零点がa=0.5から等距離のところに並ぶことになります。ところが、実虚線、虚実線で考えると、それでは困ったことが生じます。
実虚線よりも、虚実線のほうが図として見やすいので、そちらで説明しますが、虚実線上の実部はマイナスからプラスへと増加しています。単調増加のように見えますが、r番目の虚実線では単調増加が壊れて、波の山が出来て、零となる場所がふたつ存在したとします。すると右図のようになるはずですが、ふたつ目の零点のあと、実部線はマイナスになります。ところがこの線はやがてプラスにならなければなりません。しかし、プラスになるためにはもう一度零点を通らざるを得ません。結果的に、零点がふたつということはあり得ず、必ず３つ存在することになります。
３つ存在するとなると、x3の零点に対して、k(1-s)=0が成り立たなければなりませんから、x4=0となる第４の零点が発生し、x4があるなら、もう一度零点を通らなければならないので、第５の零点が存在することになります。このような論理の連鎖は無限に続くので、そのようなことはあり得ないことが判ります。
この矛盾を避ける唯一の道は、３の零点のうちひとつがa=0.5上にあるということす。これなら、k(1-s)=k(s)ですから、矛盾は生じません。しかし、零点が３つ存在することになってしまいます。そのようなことはありえるでしょうか。
■ a>1 、0>a に零点が存在しないことの証明
さて、a=0.5と、その周りに零点が３つ存在することになりました。もちろん、これはk(s)=0が成り立つならという仮定法を前提にした推理ですから、これが成り立たないことを示すことが証明となります。
これを証明するための準備作業として、まずは a>1 に零点がないことを証明しておきます。
すでにa=2, a=4 のときk(2+bi)≠0、k(4+bi)≠0 は証明してあります。このやり方で、a>2 においてk(a+bi)>0 を証明することが出来ます。しかし、a>1となるとこのやり方ではうまくいきません。そこで、別方法をトライすることにします。
zt(x) = 2^x/(2^x-1) * 3^x/(3^x-1) * 5^x/(5^x-1) * ..... であることは良く知られています。理屈の上では、x>1で右辺は収束するので、k(x)=zt(x)となります。これを複素数に拡張し、k(s) = 2^s/(2^s-1) * 3^s/(3^s-1) * ..... とします。
ここで、2^s/(2^s-1)=0 を解くことができ、b=0, 2pi/ln(2), 4pi/ln(2), となり、a=0 となります。これ以外に零はありません。3^s/(3^s-1)=0も同じで、b=0, 2pi/ln(3), 4pi/ln(3) となり、a=0 となります。一般的に、r^s/(r^s-1)の項目でも同じ答えになります。ですから、a≠0、つまりこの証明に必要な範囲では、a>1 で零にならないことを示しています。
r番目の素数をr1とすると、f1(s)=2^s/(2^s-1), f2(s)=3^s/(3^s-1), fr(s)=r1^s/(r1^s-1) となり、k(s)=f1(s)*f2(s)*...*fr(s)と表記できます。この式で、a>1では、f1(s)≠0, f2(s)≠0, ... fr(s)≠0 であることは証明できたのですから、k(s)≠0 であると言いたいところです。しかし、零でない数を無限に掛けて零になることもあるので、もうひとつ証明を付け加えなければなりません。
そこで、複素数をベクトルとして考えて、その絶対値を検討することにします。実数の場合、１以上の数を無限に掛けて零になることはありません。零に近づく数を無限に掛けるから零になるのです。複素数も同じことで、複素数の絶対値が零に近づかない数を無限に掛けても零になることはありません。
k(s)の右側の複素数の絶対値を計算してみます。一般項 r^s/(r^s-1) において、s=a+bi ですから、P=cos(b*ln(r)), Q=sin(b*ln(r)) とすると、分母は r^a*P-1+r^a*Q*i となります。分母から虚数を取り除くためにr^a*P-1-r^a*Q*i を分子分母に掛けます。その結果を整理すると、分母は(r^a)^2-2(r^a*P)+1、分子は(r^a)^2-r^a*P+(-r^a*Q)*i となります。
複素数の絶対値は、√(a^2+b^2) ですから、fr(s)の絶対値trの２乗は、分母の(r^a)^2-2(r^a*P)+1が消えて、tr^2=(r^a)^2 となります。つまり、tr=r^a となり、rは素数、aは１以上という条件が付いているので、零になることはありません。つまり、fr(s)の絶対値は零になることはありません。ということは、f1(s)*f2(s)*...*fr(s)*... も零になることはなく、k(s)≠0 が証明されました。
さて、1<a でk(s)≠0が証明出来たと言うことは、k(1-s)/k(s)≠0ですから、0>a にも零点が存在しないことの証明にもなっています。
■ 波の構造から 0<a<1 に零点が存在しないことを証明します。
以上の証明を前提に、以下では 0<a<1 の範囲で、零点が３つ存在することがないことを証明します。・・・とは言うものの、証明は途中までですので、その点はご了解ください。
0<a<1 の範囲で、a=0.5以外に零点がないことは、直感的には「リーマン仮説を納得する方法ver2」からも明らかですが、それを直感ではなく、論理で示すにはどうするかがこれからの課題です。そこで、それをk(s)=zt(s,n)+ber(s,n)の式に立ち戻って、a=0.5近傍で小さな波が発生しないことを式の構造から証明してみたいと思います。
k(s)には実部波と、虚部波がありますが、ここでは実部波のみを取り上げます。実部の零点が３つなければ、リーマン零点が３つ存在することはないからです。
ただ、その前に、一応、k(s)の全体構造からして、あちらこちらに波が存在することを確認しておきます。k(s)だけではありません。すべての複素関数では、実部にcos、虚部にsinが現れるので、波があるのが普通であって、波がないのが特殊だと理解すべきです。ただし、その波はsin曲線を基本としているので、過度に波打つことは稀であって、普通はサイン曲線程度に波打つと理解して間違いありません。
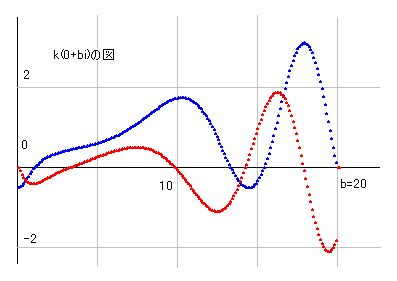
k(s)も例外ではなく、右図に見られるような波が全体的に現れます。
特徴としては、aが大きくなると波の高さがなくなり、やがて実部は１に、虚部は０に収束します。また逆に、aがマイナスの方向に大きくなると、波がますます高くなり、図示するのが困難となります。以上がY軸に沿って輪切りにしたときの特徴です。
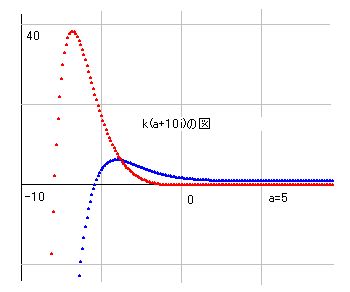
X軸に沿って輪切りにすると、aが大きいところでは波が小さくなり、マイナス部分では大きくなるという特徴がひとつの図の中で観察できます。
どちらの図の場合も、波の形は違いますが、波にリズムがあることを捉えることが出来ます。これはその他の条件で図を描いても同じことで、大きなうねりが少しづつ変化して全体の波を形成しています。突然波が激しくなることはほとんどありません。
■ 0 < a < 1 での実部波
そこで、今度は数式の分析から、 0 < a < 1 では、波の山か谷はあっても、山と谷を持つ波が生じないことを証明してみます。
k(s)の計算式を再確認しておきます。
k(s) = zt(s,n) + ber(s,n)
zt(s,n) = 1 + 1/2^s + 1/3^s + 1/4^s + ... + 1/n^s
ber(s,n) = 1/(s-1)/n^(s-1) - 1/2/n^s + s/12/n^(s+1) - s*(s+1)*(s+2)/6!/n^(s+3) + ...
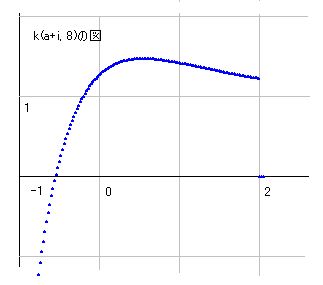
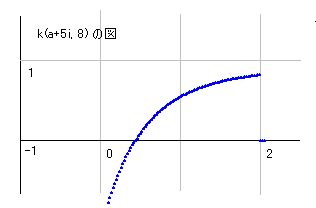
つまり、k(s)はzt(s,n)とber(s,n)を加えたものです。ですから、実部線を波として捉えると、zt(s,n)の波とber(s,n)の波がプラスされたものがk(s)の波ということになります。右図はk(a+5i,16)の図です。zt(s,n)とber(s,n)の波は値が大きいので縮小してあります。そのため、プラスした結果k(s)の波になることが明晰になっていませんが、zt(s,n)の波の値がa=-10で10^12くらいであるのに対し、k(s)の値が-2あたりであることを考慮していただければと思います。 0<a<1 の範囲ではもう少し判りやすい図になるはずです。
■ zt(s,n)
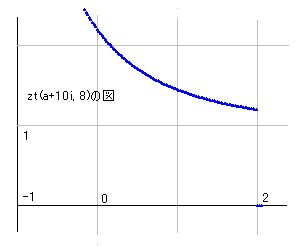
zt(s,n) の波は、0<a<1において非常に単純な構造をしています。たとえば、b=10, n=8 のとき、つまり zt(a+10i, 8) は右図のようになります。
計算式を再掲すると、
1 + cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... + cos(b*ln(8))/8^a
となります。
n→∞で、値は振動・発散して収束しませんが、k(s)としてはber(s,n)の影響で収束し、値を持ちます。実際の計算では、収束値に近い値がでるnを選んで計算するので、nを無限大にする必要はありません。
実際の計算は、b=1のとき、cos(1*ln(2))=0.7692...で、cos(1*ln(3))=0.4548...となります。この作業を続けると、まもなくマイナスの数が現れ、さらに続けるとやがてプラスに変わります。これをnになるまで計算すると答えになりますが、nをさらに大きく設定すると、またマイナスとプラスになる部分が繰り返されることになります。この繰り返しが無限に続くので、a<1では収束することはなく、必ず振動・発散します。n=8とはその一過程であるということです。ですから、nを特定するとzt(s,n)の値は確定しますが、これは仮のものでしかありません。しかし、こういうzt(s,n)の運動の構造は、nを大きくしても変化するものではありません。
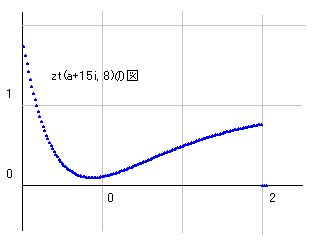
nを大きくすると計算に時間がかかるので、bの値を変えて検討を続けます。b=15のとき、つまりzt(a+15*i,8) は右図のようになります。
この場合も、図の右方向ではz1=1に収束します。nを大きくすると値はまったく変わり、b=10と似たような図も現れます。ですから、この図も変動の一過程として理解することになります。
ただ、先ほどのb=10の図との共通点は、aがプラスの無限大でz1=1に収束することです。
このzt(s,n)の実部が 0<a<1 の範囲で波にならないことは図からは明らかなのですが、これをどういう論理で証明するかがこれからの課題となります。
■ ber(s,r) の波
k(s)を構成するもうひとつの要素であるber(s,n)を分析します。s=a+biです。
ber(s,n) = Σ_[r=0,∞] B(r) * (s-1)*s*...*(s+r-2) / { r! * (s-1)*n^r }
で計算できますが、実際の計算式は次のようになります。
ber(s,n) = 1/(s-1)/n^(s-1) - 1/2/n^s +1/n^(s-1) * { B(2)*s/2!/n^2+B(4)*s*(s+1)*(s+2)/4!/n^4+...}
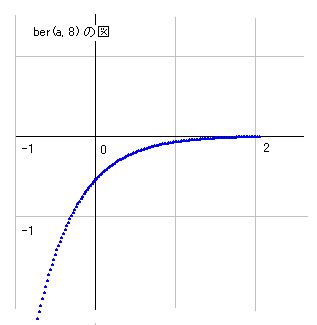
たとえば、b=10として、n=8とすると右図のような形になります。
zt(a+10i, 8) の図はすでに（３つほど前の図）載せてありますが、それと比較すると、上下逆さまにすると似ていることが判ります。k(a+10i, 8) の図は下の載せておきますが、結局、ztとberを足すと、互いにうち消し合ってk(s)に収束するはずです。図を見るだけでは明らかでありませんが、すでに多くの計算例を知っているので、これについてはこれ以上の説明は不用でしょう。
さて、ber(s,n)の実部線がどのような構造になっているかを調べます。
実部の値を計算する式は次のようになります。P=cos(b*ln(n)), Q=sin(b*ln(n)) とします。
ber(a+bi,n) = {(a-1)*P-b*Q}/((a-1)^2+b^2)*n^(a-1) -P/2/n^a + ( P*ber_a(n) + Q*ber_b(n) ) / n^(a-1)
ber_a(n)とは {B(2)*s/2!/n^2+B(4)*s*(s+1)*(s+2)/4!/n^4+...} の実部の値のことで、以下のような式として表せます。
ber_a(n) = B(2) * ra(2) / (2!*n^2) + B(4) * ra(4) / (4!*n^4) + ....
ber_b(n)は虚部の値を表す式で、以下のようになります。
ber_b(n) = B(2) * rb(2) / (2!*n^2) + B(4) * rb(4) / (4!*n^4) + ....
ここに出てくるra(n), rb(n) とはs*(s+1)*(s+2)*.... の実部と虚部のことで、B(2)*s のsの実部がra(2)で、虚部がrb(2)となります。s*(s+1)*(s+2) の実部は ra(4)、虚部は rb(4)となります。
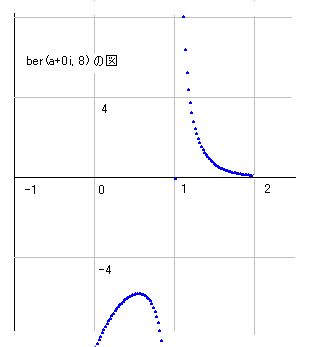このber(a+bi,n)の式で、b, n を固定して、aに対してz1を計算したときがX軸に平行な輪切りの図となります。b=0とは実数と言うことですが、それは右図のようになります。n=8 として計算しました。
b=0のとき、k(1+0i)=∞なので、それに対応してber(1+0i)も無限となっています。
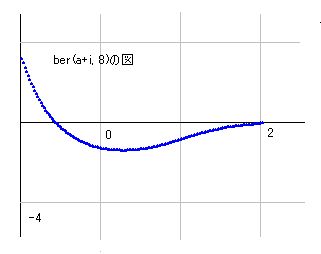b=1のときは、右図のようになります。
■ ber(s,n)の単純形
ber(s,n)の図は結構複雑なので、これをなるべく単純な形に還元して分析することにします。
ber(s,n)を計算するとき、bは固定されるので定数と見なされます。また、P/2/n^a以下の式は、aの大きさに関わらず、第１項目の式より、1/n, 1/n^2 と小さくなり、nがある程度大きいと、全体を無視できるほど小さくなります。
それゆえ、最初に登場する((a-1)*P-b*Q)/((a-1)^2+b^2)*n^(a-1)に注目して、これがどのような波になるかを確認してみます。P=cos(b*ln(n)), Q=sin(b*ln(n)) です。
この中の (a-1)^2+b^2 はa=1のときa-1=0となり、b^2が単独で影響を与えることになります。このとき、b^2は分母になるので、b<1では、b>1とは異なる大きな影響を与えます。それゆえ、b<1は別途検討することにして、ここでは b>1 という条件を付けることにします。すると、(a-1)^2+b^2 は必ず１以上のプラスになります。
n^(a-1)も１以上のプラスの値になるので、分母は必ず１以上のプラスです。
分子の中の、b*Q は b*sin(b*ln(n) ですから、aに対して定数と見なされます。
(a-1)*P = (a-1)*cos(b*ln(n)) となっています。-1<=P<=1 でプラスにも、マイナスにもなりますが、bとnが定まった時点でプラス・マイナスが決定し、途中で変化することはありません。ですから、Pも定数と見なすことが出来、結果的にこの式は1/n^(a-1)が基本形で、bの値の変化により全体が修正されるという構造になっていることが判ります。また、分子にある(a-1)により符号の変化が起きるとしても、それにより波の山か谷が出来るだけであり、山と谷を持つ波になることはありません。
このことはber(s,n)の図からも検証できます。山や谷がないことも多いのですが、b=1, n=8 ではa=0.1あたりが谷底となっています。
■ k(s) = zt(s,n) + ber(s,n)
さて、0<a<1 かつ b>1 の範囲では、zt(s,n)には波の山谷はあったとしてもひとつだけ、 （これについての証明はまだ未完成です。） ber(s,n)も、あったとしてもひとつだけであることが証明されました。k(s)はzt(s,n)とber(s,n)を加えた形になっています。この加えた結果に波の山と谷が同時に現れないことも証明が必要だろうと思いますが、これは次の課題とさせてください。加えた結果であるk(s)の図を見ても、0<a<1 の範囲で波は発生していません。
以下、k(s)の図をいくつか挙げておきます。
■ 微分による証明にトライ
波の形を分析するには微分が一番便利な気がしてきたので、遅ればせながら微分の勉強をしてみました。まだ慣れてないので、間違っているところがあるかもしれませんが、一応、教科書を読みながらやってみたところ、次の結果を得ることが出来ました。
実部を計算する式は次のものです。
1 + cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... + cos(b*ln(n))/n^a +
{ (a-1) * cos(b*ln(n)) - b * sin(b*ln(n)) } / (n^(a-1) * ((a-1)^2 + b^2)) - cos(b*ln(n)) / 2/n^a + { cos(b*ln(n)) * bera(n) + sin(b*ln(n)) * berb(n) } / n^(a-1)
bera(n)=B(2)*ra(2)/2!/n^2+B(4)*ra(4)/4!/n^4+...
berb(n)=B(2)*rb(2)/2!/n^2+B(4)*rb(4)/4!/n^4+...
B(0)=1, B(1)=-1/2, B(2)=1/6, B(4)=-1/30, B(6)=1/42, B(8)=-1/30, B(10)=5/66, B(12)=-691/2730, B(14)=7/6, B(16)=-3617/510, . . . . . . . . . . .
A=a-1, B=A^2+b^2, P=cos(b*ln(n)), Q=sin(b*ln(n)) として、これを書き直すと、
1 + cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... + P/n^a +
(A*P-b*Q)/n^A/B - P/2/n^a + B(2)*(P*a+Q*b)/2!/n^2/n^A + B(4)*{P*ra(4)+Q*rb(4)}/4!/n^4/n^A + ....
ra(2)=a, rb(2)=b で、ra(4)以下は次のやり方で計算します。
ra(r),rb(r)の計算方法を示すことにする。そのための下準備として、ka(a,b)を定義する。a,b は正の整数。
ka(0,0)=1, ka(1,0)=1, ka(1,1)=1, ka(2,0)=1, ka(2,1)=3, ka(2,2)=2,
ka(3,0)=1, ka(3,1)=6, ka(3,2)=11, ka(3,3)=6,
ka(4,0)=1, ka(4,1)=10, ka(4,2)=35, ka(4,3)=50, ka(4,4)=24,
以下略。
ka(n,r)の計算方法は、ka(n,r) = n*ka(n-1,r-1) + ka(n-1,r) です。
さて、これを前提に、ra(r), rb(r) の計算方法を説明します。
たとえば、r=4 のとき、(a+bi)^3, (a+bi)^2, (a+bi), を展開し、次のようにka(n,r)を掛け並べます。
ka(2,0) * { a^3+3a^2(bi)+3a(bi)^2+(bi)^3 }
ka(2,1) * { a^2+2a(bi)+(bi)^2 }
ka(2,2) * { a+(bi) }
この式を総計したものの、実部がra(4) 虚部がrb(4) となります。
この場合、ka(2,0)=1,ka(2,1)=3,ka(2,1)=2, ですから、
ra(4)=a^3-3ab^2+3a^2-3b^2+2a, rb(4)=3a^2b+6ab+2b-b^3, となります。
r=5 ならば、
ka(3,0) * { a^4+4a^3(bi)+6a^2(bi)~2+4a(bi)~3+(bi)~4 }
ka(3,1) * { a^3+3a^2(bi)+3a(bi)^2+(bi)^3 }
ka(3,2) * { a^2+2a(bi)+(bi)^2 }
ka(3,3) * { a+(bi) }
この場合、ra(5)=a^4+6a^3-6a^2b^2+11a^2+6a-18ab^2+b^4-aab^2
rb(5)=4a^3b-4ab^3+18a^2b-6b^3+22ab+6b
となります。
ra(6)=a^5-10a^3b^2+5ab^4+10a^4-60a^2b^2+10b^4+35a^3-70ab^2+50a^2-50b^2+24a
これを微分すると以下の式になります。
P=cos(b*ln(n)), Q=sin(b*ln(n)), A=a-1, B=A^2+b^2, と表記します。
-ln(2)*cos(b*ln(2))/2^a - ln(3)*cos(b*ln(3))/3^a - ln(4)*cos(b*ln(4))/4^a - ... - ln(n)*cos(b*ln(n))/n^a -
P*{1-2*A^2/B-A*ln(n)}/n^A/B + b*Q/n^A/B*{2A/B+ln(n)} + ln(n)*P/2/n^a
-ln(n)*B(2)*(aP+bQ)/2!/n^2/n^A+P*B(2)/2!/n^2/n^A - ln(n)*B(4)*(P*ra(4)+Q*rb(4))/4!/n^4/n^A +B(4)/4!/n^4/n^A*{P*(3a^2-3b^2+6a+2)+Q*(6ab+6b)} + ....
■ n=2 のとき
n=2 のときを証明し、n=3, n=4 と増やしてゆき、一般的なnで証明できれば、この証明は完成することになる。そういう予定のもとで、以下のように証明してみることにする。
n=2のとき、式は、1/2^(a-1)*{ P(1-2A^2/B-A*ln(2))/B+Q(2A/B+ln(2))-P*ln(2)/4 } +1/48-(3a^2-6b+6a+2)/11520+...
この場合、1/48以下は最初は無視することにする。また、1/2^(a-1)は常にプラスなので、これも無視する。残りは P(1-2A^2/B-A*ln(2))/B+Q(2A/B+ln(2))-P*ln(2)/4 となるので、これを零として、解がふたつないことを証明する。。
Pが零でなく、b<3ならば、解がひとつもないことを示すことが出来る。
b=5.78で、0>a>1 で波が発生している。（ベルヌーイ数より前までの計算。上式）これは残念ながら大問題である。こういうｂはたくさんある可能性がある。
１／４８をプラスすると零が解消される。
■ n=3 のとき
n=3 のとき、式は、1/2^(a-1)*{ P(1-2A^2/B-A*ln(2))/B+Q(2A/B+ln(2))-P*ln(2)/4 } +1/48-(3a^2-6b+6a+2)/11520+...
この場合、1/48以下は最初は無視することにする。また、1/2^(a-1)は常にプラスなので、これも無視する。残りは P(1-2A^2/B-A*ln(2))/B+Q(2A/B+ln(2))-P*ln(2)/4 となるので、これを零として、解がふたつないことを証明する
２度微分すると
(ln2)^2*cos(b*ln2)/2^a + (ln3)^2*cos(b*ln3)/3^a + ...
-(ln(n))P*/n^A/B*{ 1-2A^2/B-A*ln(n) } - 2PA/n^A/B^2 * { 1-2A^2/B-A*ln(n) }
+ P/n^A/B * { -4A/B+4A^3/B^2-ln(n) } - Q*ln(n)*b/n^A/B * {2A/B + ln(n) } -2*b*Q*A/n^A/B^2*{2A/B+ln(n)} + b*Q/n^A/B * { 2/B-4A^2/B^2 }
- (ln(n))^2*P/2/n^a - 2*P*ln(n)*B(2)/2!/n^2/n^A + (ln(n))^2*B(2)/2!/n^2/n^A*(aP+bQ)
+ (ln(n))^2*B(4)/4!/n^4/n^A * {P*(a^3-3ab^2+3a^2-3b^2+2a)+Q*(3a^2b+6ab+2b-b^3)}
- 2*ln(n)*B(4)/4!/n^4/n^A * {P*(3a^2-3b^2+6a+2)+Q*(6ab+6b)}
+ B(4)/4!/n^4/n^A * {P*(6a+6)+Q*(6b) }
0 + B(4)*(6a+6)/4!/n^4 + B(6)*(20a^3-60ab^2+120a^2-120b^2+210a+100)/6!/n^6 + ...
■ 波の要素の無い曲線同士を加減すると波の要素の無い曲線が生じる
これを証明するためには、まずその前提として「波の要素」という概念を定義します。
波とは、x=pの直線で切ったときに交点が３つ以上できる曲線のことですが、「波の要素がある曲線」とは、p*x+q=y の直線で切ったときに交点が３つ以上できる曲線です。「波の要素がない曲線」とは、その直線で切ったときに交点が３つ以上生じない曲線です。
この場合、交点の出来る範囲も考慮されます。x>0で交点が２つあり、x<0で交点が１つあるとき、全体的にはこの曲線は波となっていますが、x>0では波ではありません。たとえば、sin(x*pi/2)のサイン曲線も、x=0からx=1までの範囲では波ではなく、また波の要素もありません。
波でないのに、波の要素はある事例として、次の曲線を挙げておきます。
2*x^3+x+1=y という曲線は右図のようになっていて波ではありません。つまり、x=a という直線との交点はひとつしかありません。しかし、2x+1=yの曲線で切ると、交点が３つ生じます。ですから、波の要素はあります。
さて、同一の範囲において波の要素を持たない曲線同士を加減計算すると、その結果生じる曲線もまた波の要素を持たない曲線になります。
■ b<1 において零点がないことの証明
さて、残るはb<1 の範囲に零点がないことを示さなければなりませんが、これは零点の複素平面図から明らかであるという論理を使わせていただきます。「数式を使わないので証明ではない」と思う方もおられるかもしれませんが、実零線１と虚零線１は交わっていませんし、近づいてさえいません。また、それ以外の線が存在する可能性も零ですから、証明として使うのに差し支えないだけの明晰さがあります。
もし、こういう論理が証明として相応しくないなら、再度考えるつもりなので、ご指摘いただければと思います。
■ 結論
最後のところは尻切れトンボですが、途中まではたぶん（願わくは）正しく分析しているだろうと思います。残りは、いずれ証明を完成させて、公表できるようにしたいと願っています。
これまでのところで、論理の間違い、用語の間違い、勘違いもあるかもしれませんので、何なりとご指摘いただければ幸いです。質問などは下記のアドレスまでお寄せください。
ご感想、ご質問、その他のご意見は、Mailのアドレスへお願いします。
表紙に戻る
|