|
リーマン仮説の証明 ver15 第2部、第3部 第2部 k(1-s)/k(s)≠0 の証明 ■2の1■ k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } という式があります。この式は私が最初に発見したと思ったのですが・・・、すでに知られている式とのことで、少し残念です。しかし、それならそれで差し支えありません。複素数の階乗もガンマー関数で定義されているとのことですが、この点はまだ学びが足りないのでよく理解していません。ただ、この証明では上記の式を複素数の階乗の定義として使うことにしました。いまのところそれで何ら矛盾を起こすことはないので、問題ないと思いますが、もし、この点について間違っているなら、訂正しますので、教えていただければと思います。 さて、上記の式が正しいことはすでに承認されているとのことなので、ただちにこれを複素数に拡張して使うことにします。s=a+biとすると、 k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } となります。この式の右辺に零点が無ければ左辺にも無いことになります。そこで、右辺の式を個別に検討することにします。 なお、無限点、特異点の不存在も証明に必要になったので、この点についての証明も付け加えます。右辺に無限点がなければ、k(1-s)/k(s)に無限点はありません。また、特異点がなければ、k(1-s)/k(s)にも特異点はありません。 (補足 08/10/31) k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } の式をどのようにして求めるかを補足しておくことにします。私自身は多桁計算プログラムでの計算により見つけたので、何も説明するほどのことがなく、先のような記述になりました。しかし、再検討の結果、この式は計算によらなくても導出できることが判りました。 k(x)がベルヌーイ数で求められることは良く知られています。 k(2)=pi^2/6, k(4)=pi^4/90, k(6)=pi^6/945,... つまり、 k(x)=+-B(x)*(2pi)^x/2x! ということです。ベルヌーイ数はプラス・マイナスに変化するので、それを消すためにマイナスがつく場合があります。 この式を一般化すると、 k(x) = B(x)*(2pi)^x/2x!/sin(pi*x/2-pi/2) となり、これをB(x)について纏めると、 B(x) = k(x)*2x!*sin(pi*x/2-pi/2)/(2pi)^x となります。 さて、P=n^(x+1)とすると、Σn^x = P/(x+1) + P/2n + P*x/12n^2 - P*x(x-1)(x-2)/720n^4 +.... -x!*su(x+1) であることはすでに説明してあります。これを B(x) で表現できますが、ベルヌーイ数はB(1)=-1/2 となるので、綺麗に表記できません。そこで、ここでは数字のままにしておきます。x=1 以外は su(x)=B(x)/x! という関係にあります。 Σ1/n^x = k(x) - 1/(x-1)/n^(x-1) - 1/2n^x + 1/12n^(x+2) - ... という式もすでに知られています。 Σn^(-x) = Σ1/n^x また、Σn^x = Σ1/n^(-x) なので、k(x) = -(-x)!*su(-x+1) が成り立ち、k(x) = -B(1-x)/(1-x) となります。これを k(1-x) = -B(x)/x と整理して、先のB(x)の式を代入します。すると、k(1-x)/k(x) = -2x!*sin(pi*x/2-pi/2)/(2pi)^x/x/(2pi)^x となります。ここで cos(pi*x/2) = -sin(pi*x/2-pi/2) なので、結果として k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } という最初の式を得ます。 k(x)とB(x)は結局同じ種類の関数であることは大変面白いですね。ベルヌーイ数も複素数に拡張でき、零点がx=0.5上に存在することになります。 ■2の2■ cos(pi*s/2) 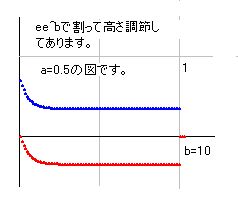
cos(pi*s/2)を複素数として計算するということは、cos(s)=1-s^2/2+s^4/4!-s^6/6!... を計算すると言うことです。これをそのまま図示すると、bの増加に伴いすぐに値が図からはみ出してしまいます。そこで、e=2.718281828として、e^bで割ることにしました。cos(pi*s/2)=z1+z2*i とし、p=e^b とすると、z1/p, z2/p が極大化せず、一定の値に収束します。これで図は非常に単純化します。a=0.5のときの図を載せておきます。 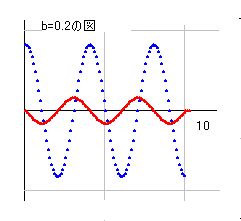 bを特定したときの形のほうが判りやすいので、そちらの図を使って説明すると、右図のように実部がコサイン曲線、虚部がサイン曲線(マイナス付きです)として現れます。これはどのbの値に対しても同じです。 右図はb=0.2のときです。次の図がb=2のときです。  b=0.2とb=2の図を比較すると判りますが、高さが異なるだけのことで、同じ構造をしています。z=0との交点については実部と虚部が交互に現れるので、交わることはありません。また、b=0.2とb=2を重ねると判りますが、実部の交点どうしは同じ場所で重なっていて、虚部は虚部で重なっています。 実部と虚部がともに零となる点は、b=0のときだけであり、z=0の所に赤の横一本線が引かれた形になります。実部は青線で、a=1, 3, 5, 7, 9 と規則正しく零になるので、ここが零点となります。 さっそく零点が見つかりましたが、ここはb=0の点なので、リーマン仮説証明の対象外の点です。しかし、無視するわけではなく、覚えておいて、あとで検討することになります。 なお、ここには、零点はあっても、無限点も特異点もひとつもありません。 ■2の3■ (2*pi)^s の証明 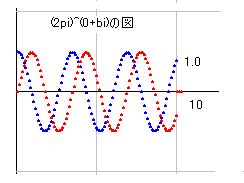 (2*pi)^s をs=a+biとして計算します。a=0,b=0のとき (2*pi)^s=1 です。b=0のときが実数で、どのaに対しても正の実数になり、零になりません。a→-∞の極限値として零になります。 bz座標で(2*pi)^sを図示しようとしたのですが、値が飛躍的に増加するので図を描けません。そこで(2*pi)^a で割ったところ、どのaに対しても同じ図になりました。右図はa=0のときのものですが、他のaでも同じ形になります。サイン曲線とコサイン曲線が綺麗に並んでいて、z=0で交わることはあり得ません。無限大になる点もありません。 次に、az座標で、任意のbに対してaが変化する図を書いてみました。すると、すべてa軸に対して平行な線が描かれます。値の変化が無いと言うことですから、零点も無限点もありません。 この式の場合は、(0,0)でも零になっていません。 ■2の4■ s の証明 s=a+bi ですから、a=0, b=0 のときが零点で、それ以外にはありません。無限点もありません。 ■2の5■ s! の証明 (1-s)!*s! という式を使います。  さて、s!はk(1-s)/k(s)を使って計算できます。その結果、s!の形がある程度判るのですが、期待したほど綺麗な形にはなっていませんでした。右図はa=10のときのb=0から10までのものですが、s!の値が巨大になっています。aの値を変えるとまた別の図になります。ですから、s!の実態を理解するのは結構面倒です。この図の場合は、bを増加させると波を描きながら小さくなっています。細部においては複雑な動きをする箇所もあり一筋縄ではいきません。これではk(s)の証明と同程度に難しそうという感想が生じてきます。 しかし、(1-s)!*s! という式を考えると、すべての問題は消え去ります。 s!= k(1-s)*s*(2pi)^s / { k(s)*2*cos(pi*s/2) } というのが、今回の証明の前提になっている複素数階乗の定義です。ですから、(1-s)!*s! もこの定義からすぐに導くことが出来ます。つまり、k(1-s)とk(s)が消えて、計算しやすい関数だけが残ります。 (1-s)!s! = (1-s)*s*pi /{ 2*cos(pi(1-s)/2)*cos(pi*s/2) } 分子の (1-s) と s は、それぞれa=1, b=0 で零、a=0, b=0 で零となります。分母のcos(pi*(1-s)/2)とcos(pi*s/2)はa=0.5を基準として左右対称の形をしているので、片方を分析すれば、もう片方も同じ結論になります。そこで、cos(pi*s/2)がどのようになっているかを調べてみます。 ■2の6■ cos(pi*s/2) cos(pi*s/2)については先ほど説明したばかりなので、そちらを参照してください。bを特定して図を描くと、実部がコサイン曲線、虚部がサイン曲線となります。ですから、b=0を除き、z=0で交わることはありません。 実部と虚部がともに零となる点は、b=0のときだけであり、a=1, 3, 5, 7, 9 と規則正しく並んでいます。 ■2の7■ cos(pi*(1-s)/2) の零点の場所 cos(pi*(1-s)/2) はcos(pi*s/2) と同じ構造ですから、零点の場所は、b=0のときだけで、a=0, 2, 4, 6 と続きます。 さて、(1-s)*!s! の零点を求めると書きましたが、証明のためには無限点の場所も含めて確認しておかなければなりません。分子が零なのは、(0,0), (1,0)のふたつで、分母が零なのは、(0,0), (1,0), (2,0), (3,0),... などの場所になります。(0,0)と(1,0)は、0/0ですから特異点となります。あとの(2,0), (3,0)... などは無限点となります。この特異点と無限点はあとで検討します。また、このことから、b≠0には零点も無限点、特異点もないことが判ります。 ■2の8■ s! の零点・無限点は? さて、(1-s)!*s!の零点・無限点の場所がすべてb=0上であることは確認できましたが、それがs!の零点・無限点の場所であると断言するわけにはいきません。なぜなら、その他の可能性がまだ残っているからです。 b≠0では必ず (1-s)!*s!≠0 かつ (1-s)!*s!≠∞ ですが、もし(1-s)!=∞ かつ s!=0 だと (1-s)!s!が零以外の有限値を取る可能性があります。ですから、s!≠0を証明するためには、(1-s)!が無限でないことの証明を追加しなければなりません。そこで、このことの証明のためにマイナスの階乗の公式を使うことにします。 ■2の9■ マイナスの階乗の公式 マイナスの階乗の公式とは、(-n)!=n*pi/n!/sin(n*pi) というものです。これが実数の範囲で正しいことは、先のページ 「第4の広場の付録・ 実数値での階乗の計算方法」 で説明してあります。ここではそれを複素数に拡張して使うことにします。s=a+bi として、 (-s)! = { s*pi } / { s!*sin(s*pi) } という式になります。 ■2の10■ sin(s*pi)の検討  右辺の中でsin(s*pi)はまだ検討していなかったので、ここでどこに零点が現れるかを見てみます。 sinの図はcosと同じ形で、X軸に平行に波が現れ、Y軸に平行に増加曲線が現れます。その増加は激しいのですが、e^bで割ると収束します。a=2.1のとき、b=0からb=10までを図示すると右のようになります。これは、実部も虚部もe^bで割った値を使っています。  b=2のとき、a=0からa=10までを図示すると、右のようになります。これもe^bで割っています。 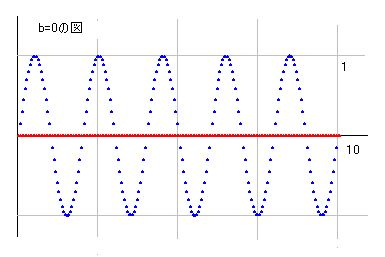 結局、実部、虚部ともに零となるのはb=0の場合のみで、a=1, 2, 3, 4... と零点が並びます。 sinが零点だと(-s)!が無限大になる可能性があります。面白いことに・・・というか、当然のことですが、実数のマイナス階乗には繰り返し無限大が現れるのと対応しています。 また、複素数なので、実数の場合とかなりの違いがあるのですが、sinで割ったとしても必ずしも零で割ることにはなりません。面白い現象ですね。 さて、マイナスの階乗公式にある分子ですが、ここにsが登場します。s=a+bi で、b≠0 が条件なので、s≠0 と書いて間違いないでしょう。 さて、これで結論になるのですが、マイナスの公式は、左辺に階乗を集めて纏めることも可能なので、書き直しておきます。分子の s を消さないようにお願いします。 (-s)!*s! = s*pi / sin(s*pi) そして、b≠0を条件に、この右辺が零にならにことを先ほど証明したのですが、合わせて無限にもならない、特異点にもならないことも証明できていることに留意しておいてください。 ■2の11■ s!≠0 の証明 (09/01/31 どうもすいません。かなりひどい誤解があったので、一部書き直しました。幸い結論は同じです。) さて、(1-s)!*s!≠0 かつ (1-s)!*s!≠∞ かつ (-s)!*s!≠0 かつ (-s)!*s!≠∞ ということまで証明できたと言うことです。これを前提に s!≠0 を証明します。条件は b≠0 だけです。 そこで背理法を使うことにします。もし、b≠0という条件で s!=0 となるところがあると仮定します。その点をs1=a1+b1*i とします。このとき、(1-s)!*s!≠0なので (1-s1)!は無限大となります。・・・とは言うものの、ここは複素数なので、「無限」の意味するところが実数と少し異なります。複素数の場合、s=z1+z2*i とすると、z1 か z2 のどちらかが無限であれば、実数の無限と似た働きをします。ですから、複素数の場合、無限大とは、z1 と z2 の両方が無限と言うことでなく、どちらかが無限であると理解しておいていただければと思います。 (1-s1)!が無限大ということなので、この場合、s!*(-s)!≠∞ を使います。(s1-1)!が普通の数とか、無限大なら、答えが∞になってしまい、前提に反します。ですから、(s1-1)!=0 でなければならないことが判ります。(s1-1)!が零なら、(1-s)!*s!≠0 の分析から(2-s1)!が無限大ということになります。(2-s1)!が無限大なら、(s1-2)!は零で、(3-s1)!は無限大となります。この作業は際限なく続くので (-a1+1,b1), (-a1+2,b1), (-a1+3,b1) と並ぶ点は無限大に、(a1-1,b1), (a1-2,b1), (a1-3,b1) と並ぶ点は零になります。b1は零ではないので、虚数ということで、s!の複素数部分にたくさんの無限点と零点が一直線に並ぶことになります。 これは起こりそうもないことですが、一応起こったとすると、これによりk(1-s)/k(s)にもたくさんの無限点と零点が生じることになります。s1!は零と仮定してあるので、k(1-s1)/k(s1)の公式に当てはめると零になります。この場合、k(1-s1)=0 もしくは k(s1)=∞ ということで、それ以外の可能性はありません。また、(s1-1)!も零ですから、k(2-s1)=0 もしくはk(s1-1)=∞ となります。この並びは無限に続くことになります。つまり、ある特定のb1に対して、その列においては実部が1増減するたびに零点、もしくは無限点が現れることになります。 ところが、以下に示すように、k(a+bi)=z1+z2*i において、lim_[a→∞]z1=1 となり、a>2においてk(s)は零にならず、∞にもなりません。つまり、k(2-s1)=0, k(3-s1)=0, k(4-s1)=0 ということが無限に続くことはありません。ここに矛盾が生じます。これで、背理法の原理により、最初の仮定である「b=0以外でs!が零になるところがある」という命題が間違っていたことになります。 なお、s!が零にならない証明と同様の方法で、s!が無限にならないことも証明できます。s!が無限ならば、k(2-s1)=∞、k(3-s1)=∞、k(4-s1)=∞ となり、limg_[a→∞]k(s)=1 と矛盾するからです。(b=0を除いています。) ■2の12■ lim_[a→∞]k(s)=1 を証明します。 xを実数としたとき、lim_[x→∞]k(x)=1 であることは自明のことと言ってもよいでしょう。これを複素数としても同じことなのですが、一応証明しておくことにします。 s=a+bi として、a>1のときk(a+bi)=z1+z2*i とします。a>1ではk(s)=lim_[n→∞]zt(s,n) が成り立つので、z1 = 1+Σ_[n=2,∞]cos(b*ln(n))/n^a および z2 = -Σ_[n=2,∞]sin(b*ln(n))/n^a となります。lim_[a→∞]cos(b*ln(n))/n^a=0、lim_[a→∞]sin(b*ln(n))/n^a=0 なので、 lim_[a→∞]1+Σ_[n=2,∞]1/n^a=1 および lim_[a→∞]Σ_[n=2,∞]1/n^a=0 が成り立ちます。これで、lim_[a→∞]k(s)=1 が証明できました。 ちなみに、a=2 のとき 1 + 1/2^a + 1/3^a +1/4^a + ... =1.6449...であることは良く知られています。k(s)の実部を計算する式は 1+ cos(b*ln(2))/2^a + cos(b*ln(3))/3^a + cos(b*ln(4))/4^a + ... です。それぞれの項目を比較すると、すべて 1>=cos(b*ln(n)) が成り立ちます。つまり、z1<1.6449 ということになり、k_re(2,b)≠∞が証明できました。 また、2-Σ1/n^a は 1 - 1/2^a - 1/3^a - 1/4^a - ... = (2-1.6449) です。cos(b*ln(n))>=-1 なので、z1>(2-1.6449) が成り立ち、z1≠0が証明できます。 a=4 のときは、k(4)=1.0823... なので、z1≠∞ を示すことが出来ます。また、z1>(2-1.0823) から z1≠0 となります。a=6でも、8でも同じです。 このやり方でaが2以上のすべての数において、z1≠0 と z1≠∞ を示すことが出来ます。 ■2の13■ k(1-s)/k(s) の零点の場所 これで k(1-s)/k(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } の右辺にあるすべての項目を検討したことになります。右辺の式が b=0上以外で零にならず、無限にも、特異点にもならないのですから、k(1-s)/k(s)も、b=0以外で、零にも、無限にも、特異点にもならないことが証明されたことになります。 ここでb=0上の零点の場所を再確認すると共に、それがk(1-s)/k(s)にどのように反映されているかを確認しておきます。 まずは、(1-s)!*s! = (1-s)*s*p /{ 2*cos(pi(1-s)/2)*cos(pi*s/2) } の式を再確認しますが、このとき、右辺の分母が零となるのが、b=0上のところだけで、a=0,1,2,.... とつづきます。ですから、(1-s)!s!では無限点となります。分子が零のところは、(0,0), (1,0) ところですが、分母が零なので、(1-s)!*s!がどうなるかは不明です。 s!については、(0,0), (1,0) については、この式からはどうなるか不明ですが、別の計算式から、0!=1, 1!=1 ということが判っています。b=0とは実数ということで、 (-2)!, (-3)!, ... と見てゆくと、すべて無限大になることを示しています。これは、従来のマイナス階乗の理解と一致しています。 さて、k(1-s)/k(s)の右辺分母は s*(2*pi)^s ですが、零となるのは(0,0)だけです。また、無限になる点はありません。 右辺分子の零点は、s!には無く、cos(pi*s/2)の零点は b=0で、(1,0), (3,0), (5,0), (7,0),. . . と並んでいます。マイナス方向にも (-1,0), (-3,0), (-5,0), . . . と並びます。無限点については、s!の場合、(-1,0), (-2,0), (-3.0), (-4,0), . . . で、cos(pi*s/2)にはありません。この中で、(-1,0) を検討してみると、右辺が無限*零となり、計算不能です。左辺は k(1-s)/k(s) で計算すると -pi^2*2=-19.7392088 という綺麗な数字になっています。(-2,0) は、右辺は無限ですが、この (-2)! は+-∞なので、プラスでもなく、マイナスでもありません。結局、左辺で計算すると零となっています。(-3.0)は、右辺に零*無限があるので不定、左辺で計算すると pi^4*4/3 となります。以下、同様に分析可能ですが、結構綺麗に並んでいるところは面白いと思います。 さて、ここでひとつ説明が必要なことは、k(s)の場合はa=0.5上に零点があることになっています。ところがk(1-s)/k(s)の右辺にはa=0.5上に零点も無限点もありません。証明とは直接関係ありませんが、a=0.5の零点がどこから来るかを説明しておくことにします。 k(1-s)/k(s)はa=0.5を基準に対照で、a=0.5では同じ値どおしを割ることになり、必ず(1, 0)という答えになります。問題は、このk(s)の特徴としてa=0.5上に零点があることです。この零点においては、0/0ということになり、左辺は計算できませんが、右辺ではそれが解消されているということです。 ■2の14■ k(1-s)/k(s)≠0のとき、k(s)≠0と言えるか? さて、k(1-s)/k(s)≠0 が証明できたと言うことは、リーマン仮説証明の半分くらいが出来たと言うことを意味します。そこで、k(1-s)/k(s)≠0 を前提に残りの半分を証明することにします。 k(1-s)/k(s)≠0 であるからと言って、ただちにk(s)≠0 と結論を出すわけにはいきません。なぜなら、k(1-s)=0 のとき、k(s)=0である可能性があるからです。そこで、このふたつを一緒に証明することにします。つまり、k(1-s)≠0 かつ k(s)≠0 を纏めて証明します。 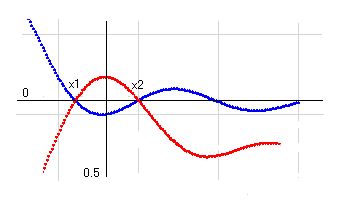 少なくとも、k(1-s)/k(s)から導き出せる結論は、「もし、リーマン零点があるなら、必ずa=0.5を基準として、左右等距離のところにペアで存在する」と言うことです。右図は、あえてふたつ並ぶように作図したものです。ペアというのは、ふたつだけでなく、偶数個であるなら許容されます。4つでも、6つでも、それぞれが等距離のところにあるなら許されます。ペアにならないようなところに存在することはありません。このことはリーマン仮説証明にとって大きな一歩です。これから、この命題を仮定法の前提として、この命題がどのような矛盾を抱えて、成り立たないかを示すことにより、このリーマン仮説証明を完成させたいと考えています。 なお、k(1-s)/k(s)には無限点はありません。しかし、k(1-s)=∞ で k(s)=∞ ならば k(1-s)/k(s)≠∞ ということもありえます。つまり、無限点も、もし存在するならペアでなければならないことになります。 また、k(1-s)/k(s)に特異点はありません。特異点とは微分不可の点のことですが、無限点は必ず特異点となります。それ以外の特異点もあり得ますが、k(1-s)/k(s)にはどの特異点もありません。しかし、k(1-s)とk(s)には特異点がある可能性を排除できないので、特異点も無限点についてと同様、ペアでの存在の可能性が排除されていないということになります。それゆえ、証明の過程では、特異点もペアで存在することを許容しつつ、それ以外に発生しないことを根拠として使うことにします。 第3部 a<0、 1<a に零点が存在しないことの証明 ■3の1■ 複素数関数 k(s)で a>1 に零点がない さて、次の証明に移る前に、a>1 に零点がないことを証明しておきます。 すでにa=2, a=4 のときk(2+bi)≠0、k(4+bi)≠0 は証明してあります。このやり方で、a>2 においてk(a+bi)≠0 を証明することが出来ます。しかし、a>1となるとこのやり方ではうまくいきません。そこで、別方法をトライすることにします。 zt(x) = 2^x/(2^x-1) * 3^x/(3^x-1) * 5^x/(5^x-1) * ..... であることは良く知られています。理屈の上では、x>1で右辺は収束するので、k(x)=zt(x)となります。これを複素数に拡張し、k(s) = 2^s/(2^s-1) * 3^s/(3^s-1) * ..... とします。 ここで、2^s/(2^s-1) を分析すると、b=0, 2pi/ln(2), 4pi/ln(2), . . . 、かつ、a=0 で分母が零となります。分子が零になることはありません。3^s/(3^s-1) も同じで、b=0, 2pi/ln(3), 4pi/ln(3) 、かつ、a=0 で3^s=1ですから、分母が零、分子は零になりません。一般的に、r^s/(r^s-1)の項目でも同じ結果になります。ですから、rを素数とすると、r^s/(r^s-1) は a>1 という条件が付くなら零になることはありません。 r番目の素数をr1とすると、f1(s)=2^s/(2^s-1), f2(s)=3^s/(3^s-1), fr(s)=r1^s/(r1^s-1) となります。k(s)=f1(s)*f2(s)*...*fr(s)と表記することにします。この式で、a>1では、f1(s)≠0, f2(s)≠0, ... fr(s)≠0 であることは証明できたのですから、k(s)≠0 であると言いたいところです。しかし、零でない数を無限に掛けて零になることもあるので、もうひとつ証明を付け加えなければなりません。 そこで、複素数をベクトルとして考えて、その絶対値を検討することにします。実数の場合、1以上の数を無限に掛けて零になることはありません。零に近づく数を無限に掛けるから零になるのです。複素数も同じことで、複素数の絶対値が零に近づかない数を無限に掛けても零になることはありません。 k(s)の右側の複素数の絶対値を計算してみます。一般項 r^s/(r^s-1) において、s=a+bi ですから、P=cos(b*ln(r)), Q=sin(b*ln(r)) とすると、分母は r^a*P-1+r^a*Q*i となります。分母から虚数を取り除くためにr^a*P-1-r^a*Q*i を分子分母に掛けます。P^2+Q^2=1 なので、結果を整理すると、分母は(r^a)^2-2(r^a*P)+1、分子は(r^a)^2-r^a*P+(-r^a*Q)*i となります。 複素数の絶対値は、√(a^2+b^2) ですから、fr(s)の絶対値をtrとすると、分母の(r^a)^2-2(r^a*P)+1がひとつ整理されて、tr^2=(r^a)^2/{(r^a)^2-2(r^a*P)+1} となります。 このtrの分母は、x=r^a と表記すると、x^2-2P*x+1=(x-P)^2+1-P^2 であり、Pの絶対値は1以下なので、(1-P^2) は必ずプラスになります。(x-P)^2 もプラスなので、x^2-2P*x+1 も必ずプラスとなり、零となることはありません。また、分子の x^2 も1以上の数になり、マイナスや零になることはありません。つまり、tr^2が、マイナスや零にならないことが確実となりました。 ここで、tr^2の分子・分母をx^2で割ることにします。tr^2 = 1/{1-2P/x+1/x^2} となります。このxは1より大きいのでrが大きくなればなるほど巨大化します。すると、2P/x と 1/x^2 は限りなく零に近づくので、tr^2は限りなく1に近づくことになります。 つまり、fr(s)の絶対値は零になることはなく、rが大きくなればなるほどfr(s)の絶対値は1に近づくので、f1(s)*f2(s)*...*fr(s)*... が零になることはなく、k(s)≠0 が証明されました。 さて、1<a でk(s)≠0が証明出来たと言うことは、k(1-s)/k(s)≠0ですから、0>a にも零点が存在しないことの証明にもなっています。 ■3の2■ a>1 に実部の零点がない 以上は複素数を前提にした証明ですが、実数値も零になることがないことを証明しておこう・・・と思ったのですが、なぜかうまくいきません。複素数が出来たのだから、実数ならもっと簡単だろうと思ったのですが、そう甘くはないようです。 実数値が零にならないことは、k(s)の実部計算から明らかで、a=∞ですべてy=1となります。マイナスが現れるのはa=0.7あたりまでで、a>1 で零やマイナスにはなりません。計算上はそれでよいのですが、証明としては何らかの論理が必要となります。 結局、実部の証明のためには、複素数の証明とは別の論理を探さなければならなくなりました。一見簡単に見える a>1 での実部の証明に手こずるとは、驚かされます。こういうところが数学の面白さだと感じるのは私だけでしょうか。 a>2 での証明はすでに先のところで完了しています。また、この証明はリーマン零点証明に直接関係するものではないので、このくらいにしておきますが、少しだけ、証明の難しさを説明しておきます。ここで言う実数値とは、s=a+bi におけるa のことなので、元になる式は k(s) = 2^s/(2^s-1) * 3^s/(3^s-1) * ..... であることに変わりありません。当初、この式での実数値だけを表した式を k(a)として、k(a)= f1(a)*f2(a)*f3(a).... という論理を使おうとしましたが、これは失敗しました。なぜなら、虚部の値によってk(a)の値が変動するからです。f1(a), f2(a),... ということでなく、あくまで最後のk(s)の実部値を調べなければなりません。そこが面倒なところです。 そこで、今度は、k(s)=zt(s,n)+ber(s,n) という式から証明してみようとしたのですが、こちらも 「計算上はそうなる」 という結論を得ることは出来ますが、証明としての論理が見つかりません。証明できないと言うことはないはずなので、どなたか証明してみてはどうでしょうか。 証明の第1部 証明の第4部 証明の第5部 証明の第6部 ■ ver15 履歴 09/01/31 ■2の9■のマイナスの階乗公式について説明不足のところがあったので、■2の10■の末尾に解説を付け加えました。それにともない、■2の11■ s!≠0 の証明 の中での私の理解不足な表現を訂正しました。複素数の場合、「零で割るから無限になる」とは言うべきではないですね。 表紙に戻る ご感想、ご質問、その他のご意見は、Mailのアドレス(hirokuro@kana.club.ne.jp)へお願いします。 |