kv_p3(s)　による証明

ver60.3　　　　new 2017/08/07





ver60 (2017/06/17)は失敗でした。・・・とは言うものも、ver60の修正版を用意しつつあるので、完全失敗ではありません。ver60での中核として考えていた kv_p3(s) による証明は不充分であることが判明しました。新しいアイデアはその続きとなるものですが、kv_p3(s) を一度終了させたうえで、新しい版として始めることにします。

ver60のどこがどのように失敗したかは、以下の説明の中で赤字で記してあります。

公表しませんでしたが、ver60.2 という証明もありました。これは、kv_p3(s)の実零線を加えて分析した証明ですが、ver60 は虚零線だけの証明です。どちらも結局は失敗に終わりましたが、失敗は成功の始まりでもあります。近いうちに新しい証明をアップさせたいと思っていますので、ご期待ください。

２０１７・８・７





ver60.3　では、ver60で省いた連続性の説明と、どこに失敗の原因があるかを付け加えてあります。








■　　　　　　k_p3(s)　の定義


k_p3(s)は、k(s)の部分関数です。p3は計算深度（精度）をあらわす数字ですが、この深度を変数としてとらえたものがk_p3(s)となります。

具体的には、k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }　というk(s)の式を分解して、nまで計算した式を p3=n と考えます。ただし、ber(s,n)は無限式なので、これも有限な式に変更します。

zt(s,n) = 1 + 1/2^s + 1/3^s + . . . + 1/n^s

ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

ber(s,n)の r はp3の別名で、便宜上、rとnを同じ数にして、これをp3と書き表します。つまり、k_p3(s) = zt(s,p3) + ber(s,p3) 、かつ r=p3 ということです。

このp3は r なので、自然数として扱われてきました。しかし、k_p3(s)を連続した関数にするために、p3を実数として扱わなければなりません。上記の式では連続関数にならないので、ここでは工夫が必要になります。





■　　　　　　zt(s,n)を連続にする。


そこで、まずは zt(s,n)　を連続になるよう修正します。

このままではnが実数のとき計算できません。そこで、zt(s,n) = 1+... + 1/(n-r)^s + 1/(n-r+1)^s + ... + 1/n^s　と理解してみます。たとえば、n=3.1のとき、zt(s,n)=1 + 1/1.1^s + 1/2.1^s + 1/3.1^s　ということです。しかし、これでは自然数のところで連続性が壊れます。そこで、0から1に変化するものがあればよいのですから、さらに修正して、zt(s,n) = (0.1) + 1/1.1^s + 1/2.1^s + 1/3.1^s　と理解します。これで連続性は確保されます。ただし、式としての統一性は崩れ、本来の zt(s,n)　とは別物になってしまうことは踏まえておかなければなりません。ただし、nが自然数のときは　zt(s,n)と一致するので、問題はありません。

上記の連続性のある zt(s,n) を数式で表現すると、以下のようになります。

nの小数点以下をp1 とし、小数でない部分をp2 とすると、zt(s,n) = p1 + Σ_[r=1,p2] 1/(r+p1)^s ということです。






■　　　　　　ber(s,n)を連続にする。


rは自然数なので、このままでは連続にはなりません。しかし、B(r)もr!も連続です。r=0のとき、B(0)=1 , r!=1 ですから、1/(s-1) を維持しつつ、r=-1のときに零になるような関数を考えればよいことになります。幸い…というか、当然というか、r=-1のときを計算することは可能で、ber(s,n)=0　となります。ですから、この式のまま連続になっています。

ber(s,n)をr=-1から計算するということです。 ber(s,n) = Σ_[r=-1,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

(-1)!=∞ですから、1/(-1)!　は零となり、全体も零となります。これですべてうまくいくはずと思ったのですが、もうひとつ問題が残っていました。それは　B(1)が　1/2 なのか　-1/2 なのかという問題です。本来のber(s,n)式ではB(1)のところを -1/2 にして計算するので問題ないのですが、B(r)を実数として計算するとB(1)が1/2になってしまいます。連続して計算するので、B(1)だけを手動でマイナスにすることができません。そこで、B(1)だけをマイナスにし、あとはそのままにする方法として　(-1)^r　を導入することにします。(-1)^rは、rが偶数のときは１となりますが、奇数のときは -1 です。ベルヌーイ数は奇数のとき、B(1)を除いてすべて０ですから、マイナスの影響はありません。ただ、B(1)だけがマイナスになるので、ber(s,n)が実数化しても連続することになります。

n=3.1 とします。すると、少数点以下は　p1=0.1　なので、p1-1=-0.9　となります。

ber(s,n) =

(-1)^(-0.9) * B(-0.9) * (s-2-0.9)! / (-0.9)! / (s-1)! / n^(s-1) / n^(-0.9)
+
(-1)^0.1 * B(0.1) * (s-2+0.1)! / (0.1)! / (s-1)! / n^(s-1) / n^(0.1)
+
(-1)^1.1 * B(1.1) * (s-2+1.1)! / (1.1)! / (s-1)! / n^(s-1) / n^(1.1)

+.....+

(-1)^3.1 * B(3.1) * (s-2+3.1)! / (3.1)! / (s-1)! / n^(s-1) / n^(3.1)

ということです。


ber(s,n) = Σ_[r=-1+p1,n] (-1)^r * B(r) * (s-2+r)! / r! / (s-1)! / n^(s-1) / n^r 　　　となります。







■　　　　　　k_p3(s) の連続性


これで、zt(s,n)もber(s,n)も連続になったので、k_p3(s) = zt(s,n) + ber(s,n) も連続ということになります。

参考までに、この式で計算した図を載せておきます。図においても連続性を確認することができます。


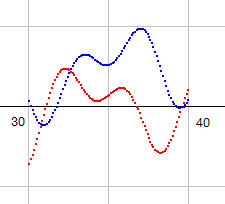
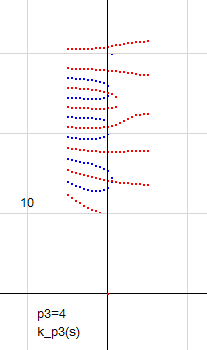
右図はp3=4 で、b=30から40までのk_p3(s)図です。この図になる直前の p3=3.99 の図が次の図です。










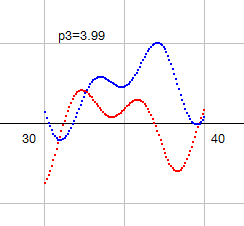
p3=3.99 だと赤線がわずかに下に位置するぐらいで、ほとんど同じ形です。














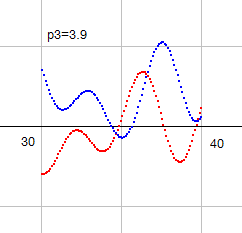
p3=3.9 にすると、ようやく違いが見えてきます。














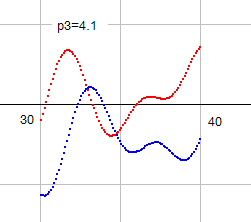
右図は　p3=4.1 とした図です。

連続性があることは認められるのではないでしょうか。











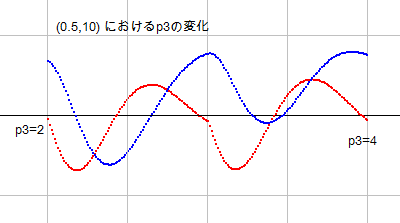
p3を変数としてみました。s=(0.5, 10) の点において、p3が　2から4 に至るまでの変化は右図のようになります。連続性は充分に認められます。

p3=3において、やや滑らかでないのは、zt(s,n)の最初の項目 p1 が式本来のものではないからです。しかし、先にも言いましたように、連続性は確保されているので、問題ありません。




k_p3(s)に連続性があるとは、kv_p3(s)も連続していることになります。






■　　　　　　kv_p3(s)　の定義


kv_p3(s) = k_p3(1-s) / k_p3(s)

p3 → ∞ がkv(s)となります。k(s)のｒが自然数のときは、kv(s)もｒに対して連続性はありません。しかし、k_p3(s)が連続となると、kv_p3(s)も p3　に対して連続関数となります。










■　　　　　　kv_p3(s)　の連続性


kv_p3(s)の定義から、連続性については明らかですが、図としても連続していることを確認しておきます。



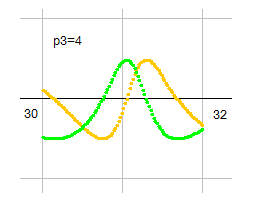
右図は　kv_p3(s) の　p3=4 で、a=0.5、b=30から32までの図です。p3をわずかに増やすと次の図になります。











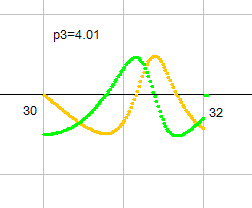
p3=4.01　とすると、わずかにずれます。













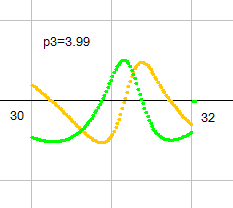
p3=3.99　とすると、逆方向にわずかにすれます。













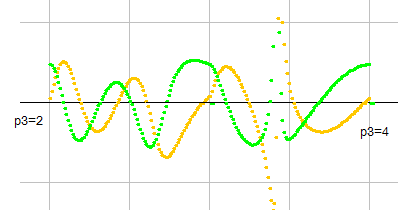
(0.5, 10) の点で、p3を変数としたときの図です。p3の連続性は充分に認められます。

p3=3.4あたりで、激しい動きがありますが、連続性に問題はありません。ただし、図を描くときには気を付けなければなりません。




kv_p3(s)の式から、すでに連続性は明らかになっていますが、図を見ても、連続性は問題ないことがわかります。






■　　　　　　k_p3(s)の零線図


p3が有限な時、k(s)とk_p3(s) では、その零線図にいくつかの違いが生じます。k_p3(s)にも実虚零点はありますが、a=0.5上に並びません。横Ｕ字形は発生しますが、右に、もしくは左にずれるとか、虚零線横Ｕ字形がないなど、いろいろあります。しかし、究極的に p3 無限大においてk(s)と一致するのですから、根本的違いがあるわけではありません。


証明に使うのは、おもに　p3=2 の場合なので、p3=2 をやや詳しく解説し、必要なところはそういう形になることをここで証明しておきます。p3=4 以上の場合も、参考までに解説します。



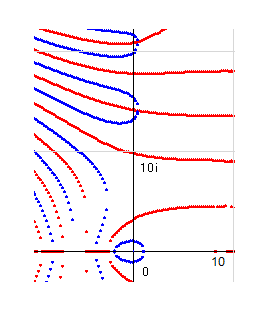
まずは、k(s)の零線図を再掲しておきます。

中央の縦軸黒線はa=0を示しています。リーマン零点の並ぶa=0.5軸は縦黒線よりやや右のところを走っています。線は引いてありませんが、青線と赤線の交点を通る縦軸です。

左無限大から実零線と虚零線が交互に下がってきます。交互であるのは、左無限大のk(s)の波がサイン曲線になることから証明できます。k(s)の絶対値を示す関数を k_r(s)　とし、k(s)/k_r(s) という関数を考えます。この関数はｂの増加とともにサイクルがやや短くなりますが、それを修正するとサイン曲線と重なります。サイン曲線の実部零の部分から実零線が流れ出し、虚部零のところから虚零線が流れ出します。ですから、出現は交互になります。

実零線はすべて横Ｕ字形になります。その理由は、右無限のk(s)の値が (1,0) に収束することです。実部１ということは、ここに実零線が到達しないことを示しています。ですから、実零線は、途中で互いに繋がって横Ｕ字形を作ります。虚零線は０ですから、右無限に到達します。しかし、到達点の間隔が左無限と異なるので、いくつかは右無限に到達できず、横Ｕ字形を作ります。

k(s)は微分係数一致関数なので、（ ver20で証明済み。） 閉鎖空間を作ることができません。ですから、特異点（singularity　無限点）のない線分の輪は存在できません。零線図(1,0) の点に輪があるのは、この点が特異点だからです。特異点はここにしかないので、輪もここ以外には存在しません。




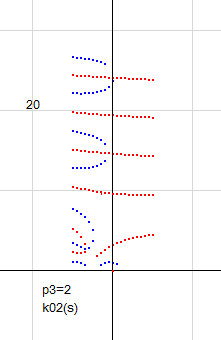
右図は　p3=2　のときのk_p3(s)の零線図です。

(0,0) 付近にできた輪、および、b=0 に到達する実零線を除いて、実零線はすべて横Ｕ字形になっているのがわかります。bの大きいところでも同じです。その理由は、k(s)と同じで、右無限の値が　(1,0) となっているからです。

その証明としては、式を挙げるだけで充分でしょう。　　　k_p3(s) = 1 + 1/2^s + 1/(s-1)/2^(s-1) - 1/2/2^s + s/12/2^(s+1)　　　s=a+b*i　です。aを増加させると、１を除いて、すべての項目が０に近づくので、実部は１、虚部は０となります。

実部が１とは、実零線が届くことはなく、実零線が途中で互いに繋がって横Ｕ字形を作ることを意味しています。

横Ｕ字形が出来ると、その間を走っている虚零線と交差するので、必ず零点が発生します。その零点ができる場所は、k(s)のように綺麗に並ぶわけではありませんが、おおむね最初のころはa=0.5の左側、そして、b=33あたりから右側に移ります。

右図の中央の黒縦線はa=0の線です。a=0.5の線は書かれてないので、零点がa=0.5の左にあるのか、右にあるのか、わかりにくい図となっています。そこで、a=0.5上の実部線、虚部線の波を表示しておきます。




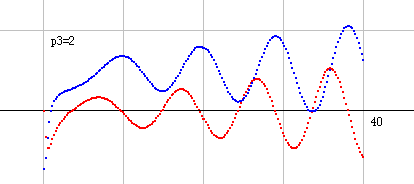
実部線がz=0より上に来ている場合が零点左側で、下に来ている場合が零点右側です。実部波はｂの増加につれ、大きくなるので、b=33以降、実部線は必ずz=0より下に来ることになり、零点は必ずa=0.5より右になります。

「必ずa=0.5より右側にある」ことについては、あとの仮定上の零点のところで使う命題なので、以下のように証明しておきます。

b=33 より上では、すべての青横Ｕ字形の中に出来る零点はすべてa=0.5より右側にあります。なぜなら、p3=2 の式は　k_p3(s) = 1 + 1/2^s + 1/(s-1)/2^(s-1) - 1/2/2^s + s/12/2^(s+1)　　となっています。この中の最大増加要因は　s/12/2^(s+1) です。この式を変形すると　s/24/2^s となり、定数である２４を除くと　s/2^s　となります。s　が増加要因で、2^s　は複素数部分をサイン波にする要因となっています。


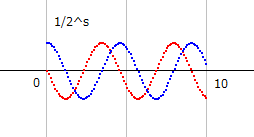
1/2^s　a=0.5　の図はサイン波になります。ですから、どんなにbが大きくなっても形は変わりません。青線と赤線は交互にz=0と交わります。青線はすべて横Ｕ字形となるので、その間を走る赤線との交点は必ず a=0.5　より右になければなりません。

1/2^s　に　s を掛けると s/2^s になります。これは　1/2^s の振動を大きくするだけですから、零点の場所はa=0.5より右であり続けます。そして、1 + 1/2^s + 1/(s-1)/2^(s-1) - 1/2/2^s の部分を付け加えても、増加要因にはなりません。考慮すべきは最初の１とs/2^s に 1/24　が付いていることです。1/24 は最初のころは大きな影響を与えるので、bが小さいときは１が一番大きな要因となります。その後、b=33で　s/24/2^s の影響が出始めると、この要因より大きな影響を与えるものが無いので、あとはすべての零点がa=0.5より右になります。



p3=4　とすると、零線図の形もk(s)に似てきます。

・・・とは言うものの、これはbが小さいところでの話です。ｂが大きくなると、零線図の形はp3=2　の形に似てきます。その理由は、p3がもともと計算精度を表す数字だからです。k(s)はp3→∞で確定しますが、p3が有限な時は、ｂが小さいところから確定してゆきます。零点を探す場合、最初のいくつかはp3=8以上で計算する必要はありません。しかし、b=100、b=1000付近のものを探すとなると、p3を上げないことには、零点がみつかりません。

このp3を固定したものが k_p3(s) です。ゆえに、p3が小さいときは、bが小さいところではk(s)と似ていますが、大きいところではk(s)からずれてきます。そして、p3を増やすと、それにつれて k(s) に近い部分が増えてくるという構造です。







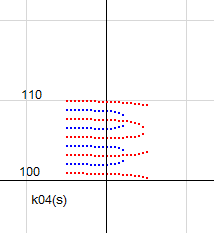
右図は　b=100　あたりの零線図です。横Ｕ字形と虚零線の交点がa=0.5よりかなり右にあることが確認できます。a=0.5上に零点がないので、この式を用いてk(s)の零点計算はできないのです。








p3=6　の場合も同じです。bが小さいところでは k(s) と似た零線図になり、bが増加すると、実零線横Ｕ字形が右に張り出してきて、p3=4, p3=2 とよく似た形になります。ただし、横Ｕ字形の幅が異なるので、同じ場所に零点ができるわけではありません。

p3=8, p3=10,　以下も同じ構造になっています。







■　　　　　　kv_p3(s)の零線図


kv_p3(s)はkv(s)の部分関数で、kv(s)=lim_[p3→∞] kv_p3(s)　という関係にあります。両者は究極的には同じものですが、p3が小さいときは零線図にかなりの違いが生じます。



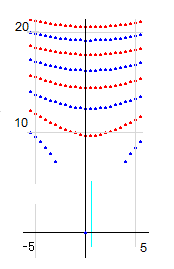
kv(s)の零線図は右図のようになっています。bの大きな部分でも形は同じです。

kv(s)には横Ｕ字形はありません。　（ ver20で証明済み。） その理由はkv(s)にb=0上以外に零点がないことです。左無限から降りてくる実零線、虚零線は、左無限の出発点がk(s)と同じなので、一対一対応しています。零点がないということは、やや下に膨れてはいますが、ひとつの線のまま右に抜けてゆくことになり、実零線と虚零線の交点は生じません。a=0.5との交点（通過点）は順次発生して、軸上の複素角度がpi/2の倍数の場所を通ります。零線が途中で戻ることはありません。kv(s)は微分係数一致関数で、b=0 以外に特異点はないので、b=0付近以外に輪が出来ることはありません。

kv_p3(s)はkv(s)と同様、微分係数一致関数ですが、kv(s)と異なり、横Ｕ字形が発生することがあり、歪みもあり、輪になることもあります。輪になるということは、そこに特異点があるからです。この特異点は　kv_p3(s) = k_p3(1-s) / k_p3(s)　という式の k_p3(s)の零点で割る場所で発生するので、定期的に発生し、それに伴って、輪も定期的に発生します。


特異点（singularity）とは無限点ですから、零線は通らないと思う人がいるかもしれませんが、実際はすべての無限点を零線が通ります。k(s)の (1,0)は無限点ですが、零線も通っています。その理由は、複素数の式が　a+b*i と表記されるからです。無限点とは　1/(a+b*i) と書くことができ、この a, b が零の時、無限となります。この式を変形させると　(a-b*i)/(a^2+b^2) となります。すると、この分子は零となっています。　0/0 ですから、全体としては零点ではありません。しかし、分子が零なので、周りから実零線、虚零線がこの無限点を目指して集まってきます。



それではkv_p3(s)の具体例を紹介しましょう。



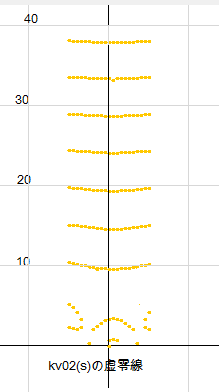
p3=2としたときの零線図は右図のようになります。

実零線は今のところ証明に必要ないので、ここでは省略させていただきます。虚零線が橙色で示されています。

線は、左無限から降りてきて、横Ｕ字形を作らず、下にやや膨らんだ形で右に抜けています。これは kv(s) と同じように見えます。ところが、拡大図を描いてみると、かなりの違いがあるのが見えてきます。

b=33あたりにわずかの歪みが見受けられますが、ここを拡大したのが次の図です。













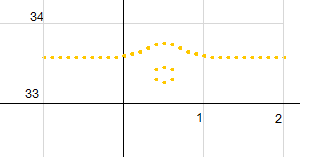
a=0.5付近に輪が出来ていることがわかります。この輪が先に説明した輪のことです。

bが大きなところでは、輪の形ははっきりしてきます。






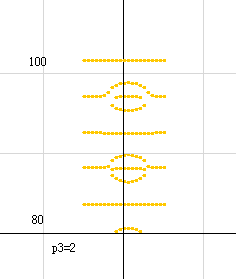
b=80 付近では、拡大しなくても輪を確認することができます。

このような輪はkv(s)には見られないものです。しかし、p3が有限な　kv_p3(s) ではごく普通のものとなっています。

どうして輪ができるかというと、先に述べたように、k_p3(s)の零点がa=0.5上にないからですが、もうひとつ重要なのは、k_p3(s)の実零線（青線）と虚零線（赤線）が通過するa=0.5上の点をkv_p3(s)の虚零線（橙線）が必ず通過することです。これは kv_p3(s)の式から証明できます。

kv_p3(s) = k_p3(1-s) / k_p3(s)　なので、s=0.5+b*i 、k_p3(s)=c+d*i とすると、kv_p3(s) = (c-d*i)/(c+d*i)　となり、右辺は　(c^2-d^2-2cd*i) / (c^2+d^2)　となります。実零線（青線）とは c=0　の線なので、実零線とa=0.5の通過点における値は -1　となり、虚部は零ですから、ここを虚零線（橙線）が通ります。虚零線（赤線）とは d=0 の線なので、赤線とa=0.5の通過点の値は 1 となり、虚部が零なので、ここを虚零線（橙線）が通ります。

青線も赤線もどちらの通過点も必ず橙線が通ることになります。

赤線と橙線は左無限から一緒に降りてくる線で、a=0.5近くでふたつの線は離れます。ですから、a=0.5上の赤線の交点を通る橙線は左無限からの線ではなく、輪になる橙線となります。


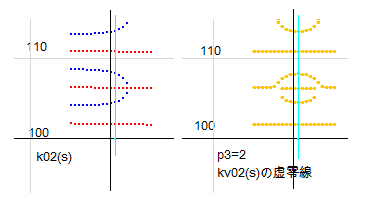
図を見るとはっきりするでしょう。右図はp3=2 で、b=100 あたりの図です。

左側は　k_p3(s) で、右側が kv_p3(s) です。赤線とa=0.5（水色線）との通過点に注目してください。左側の図で赤線が通過する場所を右図で橙線が通っていますが、その橙線は左上から下ってくる線ではなく、輪になる橙線です。





p3=4　のときも、基本的には同じ構造になっています。















p3が増加すると、bの小さいところでは収束が進み、輪が見えなくなります。

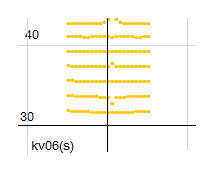
p3=4 のとき、輪が目で確認できるのは b=40　あたりからです。p3=6　になると、b=48あたりからになります。

輪が確認できるということは、a=0.5上の零点の収束が進んでいないことを意味しています。



では、収束が進んで、輪が見えなくなると零点がはっきりしてくるかというと、そうではありません。収束の前に零線図としては一時的に前より大きく混乱します。青横Ｕ字形や赤横Ｕ字形が左に抜けるなどして、橙線の輪がなくなるなどの変化が生じます。

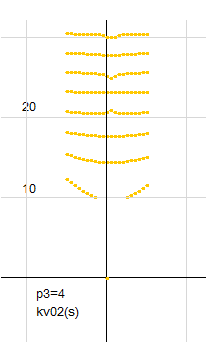
その一例が、p3=4　で b=30　あたりの零線図です。p3=2　では輪になっていたのに、p3=4 では輪が壊れています。このような大変化で、はたして連続性が保たれているのかという疑問が生じますが、p3が連続なので、このような変化も連続性の中で起きています。

p3は連続なので、輪の変化を確認することができます。p3の増加にともない、最初の輪は下のほうから順次壊れてゆくのですが、その壊れ方はいろいろです。しかし、k_p3(s)の青横Ｕ字形の間を走る赤線があるかぎり、零点は発生します。零点がa=0.5上にないかぎり、kv_p3(s) では、零点と無限点が発生します。そして、輪が移動したり、ときには消滅したりしますが、零点と無限点を通る橙線は存在していて、それが再度輪になるという複雑な動きをします。この複雑さがあるゆえに、今までその連続性を見つけることが出来なかったのですが、k_p3(s)が連続なので、零線図の変化も連続していることは確実で、それはp3を微細に変化させた零線図を描いてみると確認できます。p3=2 のときにできた輪は一度消滅することもありますが、p3がさらに増加すると、再度微細な輪が発生して、その輪がa=0.5上で縮小し、リーマン零点へと収束する形になります。

変化の仕方はかなり複雑なので、いまのところ暫定的な説明に終わることをお許しください。連続性さえ確認できれば、証明そのものに影響を与えることではありません。



変化にはいくつかのパターンがあると言えます。

ひとつの実例は、p3=2 の b=14 付近から収束にいたる零点です。ここはp3が小さいせいもあって、始めから混乱期の状況になっています。すでに青横Ｕ字形は左側に来ていて、kv_p3(s)の零点と無限点は輪ではなく、ひとつの線で繋がっています。


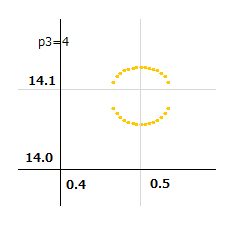
p3=4 になると、ここに輪が発生します。この輪は普通サイズの零線図では見えませんが、拡大すると見つかります。同じ輪ですが、bが大きなときの輪ではなく、収束に向かう小さな輪です。p3が増加すると、この輪は縮小して、14.1347 に収束します。









もうひとつは、p3=4 の b=30 あたりにある橙線がa=0.5を通過しなくなる事例です。このときの零線図はすでに少し前の図と同じものなので、そちらを参照してください。p3の増加により、通過が復活し、その際に小さな輪が出来ます。


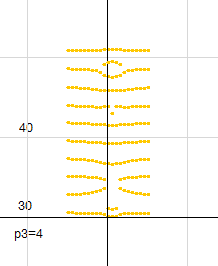
右図はp3=6のときの零線図です。通過が復活し、b=33あたりに小さな輪が発生していることが確認できます。この輪はp3の増加にともない、縮小し、ついにはa=0.5上で収束してリーマン零点となります。

気を付けるべきことは、p3を増加させるとkv_p3(s)の橙線は下に下がります。最初の頃は下がり方が大きいのでどの線がどの線に変化するかが判りにくい構造になっています。その際の判定方法は、左無限から降りてくる虚零線を数えることです。線は移動しますが、数は不変であり、途中で発生する輪になる線は含まれていません。

p3=2 で、左無限を出てa=0.5に到達する線を数えると、b=50以下に９本あります。k_p3(s)もkv_p3(s)も同じ数です。p3=4 になると、１６本に増えます。p3=6 になるとあまり変化しなくなります。p3=8 だとまったく変化しているようには見えません。


その他、p3=2 のときに出来た大きな輪がそのまま収束してリーマン零点になることがあるかもしれません。まだ検討した事例が少ないので、また別の収束の形があるかもしれません。しかし、いずれにせよ、すべて連続した変化により収束します。この連続した変化は、仮定上の零点がある場合にも当てはまります。





■　　　　　　仮定上の零点がある場合


さて、上記の説明は零点がa=0.5上に収束する場合です。仮定上の零点のときはまた別の形になります。零点は a=0.5 上で収束するわけではなく、ふたつの零点が　a=0.5から等距離の場所に収束します。それぞれ別の青横Ｕ字形の零点です。

そこで、仮定上の零点が発生している零線図を想定します。青横Ｕ字形がふたつ並ぶことは確定していますが、どのように並ぶかでいくつかの可能性が生じます。今回は、ver20で確定した形を用いますが、これ以外の形は、今回の証明が概ね正しいと判ってから取り組むことにします。もし、このひとつで矛盾を指摘することに失敗するなら、他の形でトライすることは無意味だからです。


ver20 で確定したのは右図のような形をした零線図です。下にある青横Ｕ字形が左にあり、上側の青横Ｕ字形が右に張り出して並んでいます。黒い点がリーマン零点です。

（注　　　右図はやや特殊な零線図で、緑線がkv(s)の実零線、桃線が虚零線を表しています。通常はお椀の底のような形になるのですが、それを強制的に平らに変更したときの零線図です。普通の零線図と位相的に同じものですので、ご了解ください。）


左無限から下ってくるk_p3(s)とkv_p3(s)の虚零線は一対一対応していて、aのマイナス部分ではp3の変化に対してだいたい同じ動きをします。k_p3(s)の虚零線では必ずひとつおきに零点が発生します。これは k(s) と同じ現象です。p3が変わると、零点の場所は変化しますが、p3が連続なので、零点の変化も連続です。途中で、消滅したり、融合したりすることはありません。ですから、p3=2のときに発生した零点のどれかふたつがp3→∞において仮定上の零点に変化することになります。



p3→∞で仮定上の零点となるふたつ零点はp3=2 の零線図のどこかにあります。計算可能な領域には見つかりませんから、それ以上の巨大数部分にあると想定されます。巨大数とはb=33より大きいので、その零点は a=0.5より右にあることになります。p3が増加すると、下の青横Ｕ字形は左に動き、上の青横Ｕ字形は右に動き、下の青横Ｕ字形はa=0.5を超えて左に移動します。また、赤線も上下が繋がって横Ｕ字形になり、左に移動します。そして、p3が無限大に至るとふたつの零点は仮定上の零点の場所に到着します。この変化を　k_p3(s)の零線図で考えると何ら問題が生じません。連続した移動で自然にk(s)の零線図になります。しかし、kv_p3(s) で考えると、この移動はかなりの難作業であることがわかります。kv_p3(s)には、零点だけでなく、その対称点である特異点（無限点）が存在しています。零点と特異点を結ぶ橙線があり、それが p3=2 では輪になっています。その輪はkv(s)にありませんから、p3→∞の過程のどこかで消滅しなければなりません。どのような経過で消えることが可能かを検討します。


これについては、仮定上の話なので、矛盾さえ生じなければ何をしても良いので、いくつもの可能性が生じます。そのうちのひとつでも矛盾なくkv(s)の零線図に到達できたなら証明は失敗となります。すべての可能性で矛盾が生じることを示さなければなりません。しかし、「すべての可能性」とはかなりの広範囲ですから、どのようにしたら「すべての可能性を検討した」と言えるでしょうか。これについては、いまだに検討課題として残されています。以下の分析では、主観的ではありますが、自分なりに検討した範囲でのすべての可能性において矛盾を指摘できたと考えていますが、これがすべてかどうかは今後さらに検討を続ける予定です。また、矛盾の指摘が正しいかどうかもさらに検討する予定です。

とにかく、移行する最初の図は p3=2 , kv_p3(s)零線図です。最終形は kv(s) 図です。k(s)に仮定上の零点が発生したとしても、kv(s)では　0/0　が発生して零点がなくなっています。ですから、kv(s)図は通常の零線図でなければなりません。橙線の輪はなく、横Ｕ字形もなく、お椀の底のような形の横１本線の零線図になるように変化させなければなりません。しかも、すべては連続した変化でなければなりません。


さて、それでは p3=2 から始めてみましょう。p3=2 のとき、bが大きいところでのkv_p3(s) の図は右のようになります。右図は b=80 より上の零線図ですが、それより上も同じ構造をしています。横１本線の橙線の上には、輪とその輪を補完するように、輪の外縁を形成する線があり、その上にはまた横１本線があります。

プラス・マイナスも検討事項に加えることにします。(-5,80)の点の符号は (-,-) です。これで図の内部のプラスマイナスはすべて確定できます。ちなみに (-5,100) の符号は (+,-)　となります。輪のある部分の外側下は必ず (-,+) となっています。これは仮定上の零点がある場所でも同じであると判定できます。








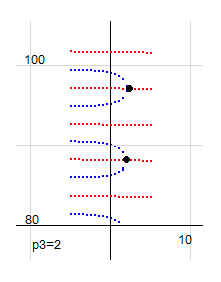
p3=2 、k_p3(s)図は右のようになっています。零点（黒点）はa=0.5上にありません。

p3が増加すると、この黒点が左に、右に移動するのですが、それは仮定上の話なので、計算で示すことはできません。しかし、そのかたちを示すことは難しくありません。











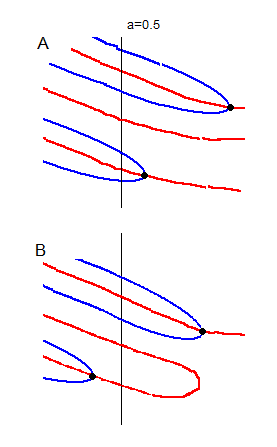
A図は零点がやや移動したときの図です。Ｂ図はさらに左、右に移動し、少しだけ仮定上の零点図に近づきました。また、赤線も横Ｕ字形にならなければならないので、この段階で横Ｕ字形になっていると想定されます。

これよりさらに仮定上の零点図に近づけることは容易です。赤横Ｕ字形がa=0.5より左に来ると、ほとんど仮定上の零点と同じになります。あとは、零点がa=0.5を基準に左右に並ぶかどうかだけです。

零点が左右に並ぶ直前の図が次のものです。








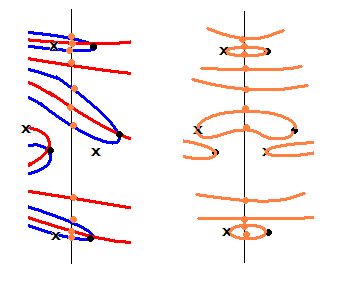
左がk_p3(s) の図で、右がkv_p3(s)の図です。k_p3(s)の零点に対して、kv_p3(s)ではその点が無限点になり、対称点が零点になります。対象点を　ｘ　で表示しておきます。この点がkv_p3(s)の零点となります。kv_p3(s) の橙線（虚零線）は零点と無限点を通ります。また、k_p3(s)の青線、赤線のa=0.5上の通り道を橙線が通ります。左から降りてくる橙線の数を変えてはなりません。この原則をもとに作図したのが右図です。

これと異なる作図も可能なので、それも検討対象ですが、今回はまず、この図において矛盾が発生することを証明します。



この図がさらに仮定上の零点図に近づくということは、左中央の零点と無限点が近づくということです。右の零点と無限点も同じです。真ん中の橙輪は、a=0.5上の青通過点、赤通過点の幅が細くならないので、橙輪の幅も細くなりません。このまま零点と無限点が合体したのが次の図です。、


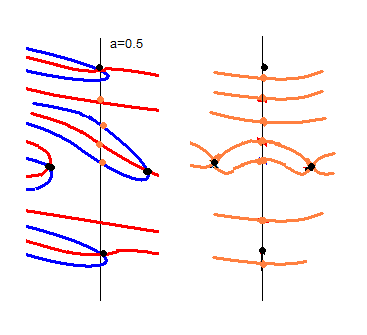
k_p3(s)からk(s)へ移行する図には矛盾はありません。しかし、kv_p3(s)からkv(s)へ移行した図は kv(s) の零線図とは異なっています。零点と無限点が合体して、零点も無限点も消滅しましたが、輪の形が残っています。kv(s)は微分係数一致関数なので、無限点のある場所以外には輪は存在できません。ところがこの図では、無限点（特異点）がなくなったにも関わらず輪だけは残っています。これは矛盾です。

また、輪が残るということは、kv(s)の図になりません。これも矛盾です。ですから、このような移動のさせ方はよろしくないということです。

他の動かし方が存在せず、必ずこの形になるなら、これで証明は完成となります。しかし、別の動かし方を見つけたので、証明はまだ完成しないことになりました。





■　　　　　　矛盾が生じない移動のさせ方（ver60.3 の追加部分）



以下のように、矛盾を生じさせない動かし方が可能であることが判りました。

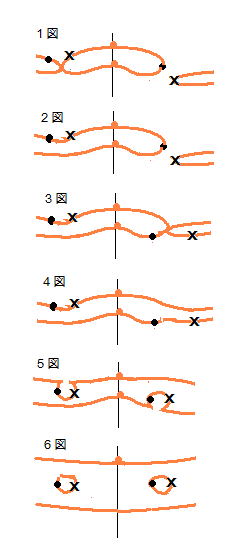
零点と無限点が合体するときに橙線輪が残っているとkv(s)になりません。そこで、合体前に最初の輪が消えるように工夫します。

まず、零点と無限点がひとつになる前に、中央の輪と橙線の横Ｕ字形が先に合体することです。合体の仕方は、零点と無限点が同じ方向の線上に位置するようにします。

右側の零点と無限点は遅れて合体させます。その理由は、同一線上にふたつの無限点があると矛盾になる可能性があるからです。この命題はまだ証明できていませんが、将来そうなる可能性もあるので、ここではそれを回避するやり方をします。ここまでが第１図から第４図までです。

このままp3→∞になると、橙線上にk_p3(s)の零点が位置することになります。するとkv(s)図になりません。そこで、無限に至る前に零点と無限点を橙線から外します。第５図は、二つ並んだ橙線上の零点と無限点がこぶのように横に張り出してくる形です。第６図でこぶが分離します。出来た輪には無限点（特異点）が付属しているので矛盾にはなりません。

そして、分離した後の輪が次第に縮小し、p3→∞で、左右同時に零点と無限点が合体し、線そのものが消滅すると、その形はkv(s)の零線図となっています。

この時のk_p3(s)が仮定上の零点が並ぶ形ですから、何も矛盾が生じないことになります。

矛盾が生じないということは、証明が成功しないということですから、別の工夫をしなければなりません。















証明の第１部

証明の第２部、第３部

証明の第４部

証明の第５部

証明の第６部

証明の第７部、第８部





表紙に戻る



ご感想、ご質問、ご意見などは、Mailのアドレス（hirokuro303@gmail.com）へお願いします。